Statistika Matematika II   »   Estimasi Interval   ›  Metode Kuantitas Pivot

Confidence Interval

Metode Kuantitas Pivot

Dalam banyak kasus, kita tidak hanya menginginkan estimasi atau pendugaan titik melainkan juga estimasi interval. Salah satu metode untuk memperoleh estimasi interval dikenal dengan metode kuantitas pivot.

Kita telah membahas mengenai estimasi atau pendugaan titik pada beberapa artikel sebelumnya serta kriteria pendugaan yang ideal. Dalam banyak kasus, kita tidak hanya menginginkan estimasi titik melainkan juga estimasi selang atau interval (confidence interval).

Salah satu metode untuk memperoleh estimasi interval dikenal dengan metode kuantitas pivot. Berikut adalah beberapa definisi terkait metode kuantitas pivot.

Location dan Scale Parameter

Langkah:

1. Dari sampel acak \(X_1,…, X_n\) tentukan estimator titik untuk \(θ\).
2. Cari bentuk kuantitas pivot.
3. Interval keyakinan (confidence interval) dapat diturunkan dari poin(2).

Note:

Kadang kita perlu melakukan modifikasi pada kuantitas pivot agar kuantitas pivot tersebut mengikuti distribusi tertentu.

Contoh Soal dan Pembahasan

Contoh 1:

Misalkan \(X_1, X_2, ...,X_n\) adalah sampel acak yang berdistribusi eksponensial dengan parameter \(θ\) (\( X_i \sim EXP(θ) \)). Dengan metode kuantitas pivot, tentukan confidence interval 100γ% untuk \(θ\) !

Pembahasan:

Pdf dari distribusi eksponensial yaitu

dan karena pdf-nya berupa bentuk \(f(x; θ)= \frac{1}{θ} f_o \left(\frac{x}{θ}\right)\), maka parameter \(θ\) merupakan scale parameter sehingga bentuk kuantitas pivotnya adalah \(Q=\hat{θ}⁄θ\).

Selanjutnya, dengan menggunakan metode maximum likelihood diperoleh estimator bagi \(θ\) yaitu \(\hat{θ}_{MLE}=\overline{x}\) sehingga kuantitas pivotnya dapat dituliskan kembali sebagai

Dengan melakukan sedikit modifikasi akan diperoleh

Fungsi \(f(q)\) tidak mengandung parameter \(θ\), sehingga \(Q\) adalah kuantitas pivot. Dengan demikian, confidence interval \(100γ\%\) bagi \(θ\) yaitu

Contoh 2:

Misalkan \(X_1, X_2, ...,X_n\) adalah sampel acak yang berdistribusi Gamma dengan parameter 2 dan \(θ\) (\( X_i \sim Gamma(2,θ) \)). Dengan metode kuantitas pivot, tentukan confidence interval 100γ% untuk \(θ\) !

Pembahasan:

Pdf dari distribusi Gamma yaitu

dan karena pdf-nya berupa bentuk \(f(x; θ)= \frac{1}{θ} f_o \left(\frac{x}{θ}\right)\), maka parameter \(θ\) merupakan scale parameter sehingga bentuk kuantitas pivotnya adalah \(Q=\hat{θ}⁄θ\).

Selanjutnya, dengan menggunakan metode maximum likelihood diperoleh estimator bagi \(θ\) yaitu \(\hat{θ}_{MLE}=\overline{x}/2\) sehingga kuantitas pivotnya dapat dituliskan kembali sebagai

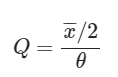
Dengan melakukan sedikit modifikasi akan diperoleh

Fungsi \(f(q)\) tidak mengandung parameter \(θ\), sehingga \(Q\) adalah kuantitas pivot. Dengan demikian, confidence interval \(100γ\%\) bagi \(θ\) yaitu

Cukup sekian ulasan singkat mengenai metode kuantitas pivot untuk memperoleh estimasi interval (confidence interval) dalam artikel ini. Terima kasih telah membaca sampai selesai. Jika Anda merasa artikel ini bermanfaat, boleh dibantu share ke teman-temannya, supaya mereka juga bisa belajar dari artikel ini.