Statistika Matematika II   »   Kriteria Estimator yang Ideal   ›  Efisiensi Relatif (Relative Efficiency) suatu Estimator

efficiency

Efisiensi Relatif (Relative Efficiency) suatu Estimator

Jika \(\hat{θ}_1\) dan \(\hat{θ}_2\) merupakan dua estimator tak bias (unbiased estimator) bagi parameter \(θ\) yang sama, kita lebih memilih menggunakan estimator dengan varians yang lebih kecil.

Kita tahu bahwa terdapat beberapa metode estimasi untuk menaksir parameter populasi yang tidak diketahui. Oleh karena itu, ada kemungkinan bahwa kita akan memperoleh lebih dari satu estimator atau penduga tak bias bagi parameter populasi yang sama. Kita tahu bahwa jika \(\hat{θ}_1\)dan \(\hat{θ}_2\) merupakan dua estimator tak bias bagi parameter \(θ\) yang sama, kita lebih memilih menggunakan estimator dengan varians yang lebih kecil.

Dengan kata lain, jika kedua estimator adalah tak bias, \(\hat{θ}_1\) secara relatif lebih efisien dibandingkan dengan \(\hat{θ}_2\) jika \(V(\hat{θ}_2)>V(\hat{θ}_1)\). Dalam kenyataannya, kita gunakan rasio \(V(\hat{θ}_2)/V(\hat{θ}_1)\) untuk mendefinisikan efisiensi relatif (relative efficiency) dari dua estimator yang tak bias.

Definisi: Efisiensi Relatif

Misalkan diketahui dua estimator tak bias \(\hat{θ}_1\) dan \(\hat{θ}_2\) bagi sebuah parameter \(θ\), masing-masing dengan varians \(V(\hat{θ}_1)\) dan \(V(\hat{θ}_2)\), maka efisiensi \(\hat{θ}_1\) relatif terhadap \(\hat{θ}_2\) yang dinotasikan dengan \(eff(\hat{θ}_1, \hat{θ}_2)\), didefinisikan dalam rasio berikut:

Jika \(\hat{θ}_1\) dan \(\hat{θ}_2\) adalah estimator tak bias bagi \(θ\), maka efisiensi \(\hat{θ}_1\) relatif terhadap \(\hat{θ}_2\) \((eff(\hat{θ}_1, \hat{θ}_2))\) adalah lebih besar dari 1 hanya jika \(V(\hat{θ}_2)>V(\hat{θ}_1)\). Dalam kasus ini, \(\hat{θ}_1\) adalah estimator tak bias yang lebih baik dibandingkan dengan \(\hat{θ}_2\).

Sebagai contoh, jika \(eff(\hat{θ}_1, \hat{θ}_2)=1.8\), maka \(V(\hat{θ}_2)=(1.8) \ V(\hat{θ}_1)\), dan kita lebih memilih \(\hat{θ}_1\) daripada \(\hat{θ}_2\). Begitu pula, jika \(eff(\hat{θ}_1, \hat{θ}_2)\) lebih kecil dari 1, katakanlah 0.73, maka \(V(\hat{θ}_2)=(0.73) \ V(\hat{θ}_1)\) dan kita lebih memilih \(\hat{θ}_2\) daripada \(\hat{θ}_1\).

Sekarang mari kita perhatikan contoh lain yang melibatkan dua estimator berbeda bagi rata-rata populasi. Anggap bahwa kita ingin mengestimasi rata-rata dari suatu populasi yang berdistribusi normal. Misalkan \(\hat{θ}_1\) adalah median sampel dan \(\hat{θ}_2\) adalah rata-rata (mean) sampel. Meskipun pembuktian tidak diberikan di sini, tapi dapat kita tunjukkan bahwa varians dari median sampel untuk \(n\) besar adalah \(V(\hat{θ}_1)=(1.2533)^2 \ V(\hat{θ}_2) \cdot (σ^2/n) \).

Dengan demikian, efisiensi relatif median sampel terhadap mean sampel, yaitu:

Berdasarkan hasil di atas terlihat bahwa varians dari mean sampel adalah mendekati 64% varians dari median sampel. Oleh karena itu, kita akan lebih memilih menggunakan mean sampel sebagai estimator bagi rata-rata atau mean populasi.

Contoh 1:

Misalkan \(Y_1,Y_2,…,Y_n\) menyatakan sampel acak dari distribusi uniform dengan interval \((0,θ)\). Diketahui dua estimator tak bias (unbiased estimator) bagi \(θ\) adalah

di mana \(Y_{(n)}=\max⁡(Y_1,Y_2,…,Y_n)\). Carilah efisiensi relatif \(\hat{θ}_1\) terhadap \(\hat{θ}_2\).

Pembahasan:

Karena tiap \(Y_i\) mempunyai distribusi uniform pada interval \((0,θ)\), maka

Dengan demikian,

Karena \(E(\hat{θ}_1)=θ\), maka \(\hat{θ}_1\) adalah estimator tak bias seperti klaim pada soal di atas. Selanjutnya, varians dari \(\hat{θ}_1\) yaitu

Untuk mencari mean dan varians dari \(\hat{θ}_2\), ingat bahwa fungsi kepadatan peluang \(Y_{(n)}\) diberikan oleh:

Oleh karena itu,

Karena \(E(\hat{θ}_2)=θ\), maka \(\hat{θ}_2\) adalah estimator tak bias seperti klaim pada soal di atas. Untuk mendapatkan varians dari \(\hat{θ}_2\), kita perlu mencari \(V(Y_{(n)})\) terlebih dahulu, yakni:

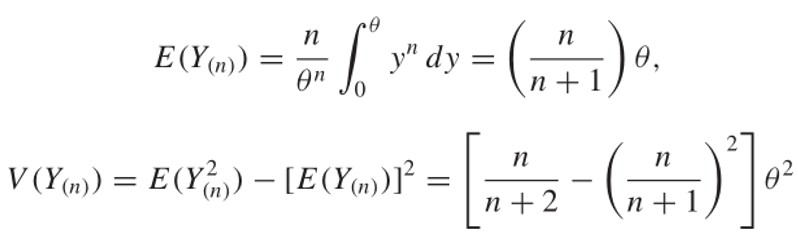
Selanjutnya, kita peroleh

Dengan demikian, efisiensi \(\hat{θ}_1\) relatif terhadap \(\hat{θ}_2\) diberikan oleh:

Efisiensi ini lebih kecil dari 1 jika \(n > 1\), yakni jika \(n > 1, \ \hat{θ}_2\) mempunyai varians lebih kecil daripada \(\hat{θ}_1\) sehingga secara umum \(\hat{θ}_2\) akan lebih dipilih sebagai estimator bagi \(θ\).