
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
STATISTIKA MATEMATIKA II
Statistika Matematika II
Pendugaan Titik
Kriteria Pendugaan yang Ideal
Pendugaan Interval
Statistika Matematika II » Kriteria Estimator yang Ideal › Pengertian dan Rumus Mean Squared Error (MSE)
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552
mean squared error (MSE)
Pengertian dan Rumus Mean Squared Error (MSE)
Salah satu kriteria untuk memilih estimator terbaik di antara estimator yang ada adalah berdasarkan mean squared error (MSE) atau kesalahan kuadrat rata-rata dari estimator tersebut.
Sebagaimana telah kita ketahui bahwa terdapat beberapa metode untuk memperoleh estimator bagi parameter populasi yang ingin diestimasi, misalnya metode momen, metode maksimum likelihood, dan metode Bayesian.
Estimator yang dihasilkan dari beberapa metode estimasi tersebut bisa berbeda. Tentu saja, ada kemungkinan bahwa meskipun menerapkan metode estimasi yang berbeda, estimator yang dihasilkan akan tetap sama. Namun, dalam banyak kasus, menerapkan metode estimasi yang berbeda akan memberikan estimator yang berbeda pula.
Oleh karena itu, kita perlu sejumlah kriteria untuk memilih estimator terbaik di antara estimator yang ada. Salah satu kriteria tersebut adalah berdasarkan mean squared error (MSE) atau kesalahan kuadrat rata-rata dari estimator tersebut.
MSE digunakan untuk mengukur kesesuaian atau kedekatan sebuah estimator \(\hat{θ}\) dari parameter \(θ\). Misalkan \(\hat{θ}\) merupakan estimator bagi parameter \(θ\) yang tidak diketahui dari sampel acak \(X_1,X_2,…,X_n\). Dengan demikian, deviasi \(\hat{θ}\) terhadap nilai sebenarnya dari \(θ\), yakni \(|\hat{θ}-θ|\), dapat digunakan untuk mengukur kualitas estimator tersebut, atau kita bisa menggunakan \((\hat{θ}-θ)^2\) untuk tujuan mempermudah penghitungan.
Karena \(\hat{θ}\) adalah sampel acak, maka kita seharusnya mengambil rata-rata untuk menghitung kualitas dari estimator. Oleh karena itu, kita peroleh definisi bagi MSE sebagai berikut.
Definisi:Mean Squared Error (MSE)
Misalkan \(\hat{θ}=u(X_1, …, X_n)\) adalah estimator bagi parameter \(θ\), maka mean squared error (MSE) dari \(\hat{θ}\) didefinisikan sebagai
\[ MSE(\hat{θ}) = E(\hat{θ}-θ)^2 \]
Perhatikan bahwa kita bisa menjabarkan rumus MSE pada definisi di atas menjadi:

Jadi, yang mau disampaikan di sini ialah bahwa MSE terdiri dari 2 komponen, yakni
- Varians, yang mengukur variabilitas dari estimator (precision)
- Bias, yang mengukur keakuratan dari estimator (accuracy)
Estimator yang mempunyai sifat MSE yang baik mempunyai kombinasi varians dan bias yang kecil. Jadi, untuk memperoleh estimator dengan sifat MSE yang baik, kita perlu mencari estimator yang terkontrol dalam varians dan bias.
Perhatikan bahwa untuk estimator yang tak bias, maka varians dari estimator tersebut sama dengan nilai MSE, yakni

Contoh 1:
Misalkan \(X_1,X_2,…,X_n\) adalah variabel acak bebas dan identik (i.i.d. random variables) dengan fungsi kepadatan peluang

Berdasarkan metode estimasi maksimum likelihood diperoleh estimator bagi parameter \(σ\), yaitu

Carilah MSE dari estimator \(\hat{σ}\).
Pembahasan:
Pertama, kita periksa apakah estimator \(\hat{σ}\) yang diperoleh adalah estimator yang tak bias (unbiased estimator) bagi parameter \(σ\). Untuk itu, kita menghitung \(E(|X|)\) terlebih dahulu, yakni
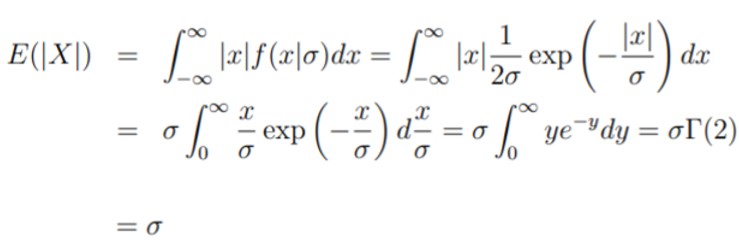
Oleh karena itu, kita peroleh:

Karena \( E(\hat{σ}) = σ \), maka \(\hat{σ}\) adalah estimator tak bias bagi \(σ\), sehingga MSE dari \(\hat{σ}\) sama dengan nilai variansnya. Untuk mencari MSE atau varians dari \(\hat{σ}\), kita perlu mencari \(E(|X|^2)\) terlebih dahulu, yakni

Dengan demikian, kita peroleh

Cukup sekian penjelasan mengenai mean squared error (MSE) dalam artikel ini. Semoga bermanfaat.
Artikel Terkait
I have had lots of troubles in my life, most of which never happened.
Mark Twain