
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
STATISTIKA MATEMATIKA II
Statistika Matematika II
Pendugaan Titik
Kriteria Pendugaan yang Ideal
Pendugaan Interval
Statistika Matematika II » Kriteria Estimator yang Ideal › Estimator (Penduga) Efisien
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552
Estimator (Penduga) Efisien
Estimator atau penduga yang efisien artinya estimator tak bias yang mempunyai ragam atau varians paling kecil. Semakin kecil varians suatu estimator, maka estimator tersebut akan semakin efisien.
Sejauh ini kita telah membahas dua kriteria estimator atau penduga yang ideal yakni ketidakbiasan dan kekonsistenan. Sekarang kita lanjutkan untuk kriteria berikutnya yaitu efisiensi. Jika ada beberapa estimator yang tak bias, maka estimator yang mempunyai ragam atau varians terkecil merupakan estimator yang paling efisien. Dengan kata lain, semakin kecil varians suatu estimator yang tak bias, maka estimator tersebut akan semakin efisien.
Untuk memeriksa apakah suatu estimator dapat dikatakan efisien, ada beberapa istilah yang perlu dipahami terlebih dahulu yakni mengenai Batas Bawah Cramer Rao (Cramer Rao Lower Bound), Informasi Fisher atau Pertidaksamaan Fisher, dan Efisiensi Estimator.
Definisi:
Misalkan \(\hat{θ}\) adalah estimator yang tak bias (unbiased estimator) bagi parameter \(θ\). Statistik \(\hat{θ}\) disebut estimator yang efisien jika dan hanya jika varians dari \(\hat{θ}\) mencapai Batas Bawah Cramer Rao (Cramer Rao Lower Bound).
Teorema: Cramer Rao Lower Bound (CRLB)
Misalkan \(X_1,…,X_n\) adalah sampel acak dengan pdf \(f(x,θ)\) untuk \(θ ∈ Ω\). Anggap \(\hat{θ}=u(X_,…,X_n)\) adalah statistik dengan rata-rata \(E(\hat{\theta})=E[u(X_1,…,X_n )]=k(θ)\) maka

di mana \(I(θ)\) adalah Informasi Fisher untuk pengamatan tunggal, yaitu
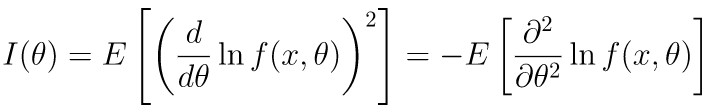
Perhatikan bahwa \( I_n (θ) \) menyatakan Informasi Fisher untuk sampel acak berukuran \(n\) dan \( I_n (θ) = n \cdot I(θ) \) menyatakan bahwa Informasi Fisher untuk sampel acak berukuran \(n\) sama dengan \(n\) dikali dengan Informasi Fisher untuk pengamatan tunggal \( (I(θ)) \).
Teorema (lanjutan)
Jika \(\hat{\theta}=u(X_1,…,X_n)\) adalah estimator yang tak bias dari \(θ\), maka \(k(θ)=θ\). Sehingga pertidaksamaan Cramer Rao menjadi
\[ Var(\hat{θ}) \geq \frac{ 1 }{n \cdot I(θ)} \]
Fungsi \( \frac{ 1 }{n \cdot I(θ)} \) sering disebut sebagai Batas Bawah Cramer Rao (CRLB) pada varians suatu estimator yang tak bias.
Definisi: Efisiensi
Rasio dari Batas Bawah Cramer Rao dengan varians yang sesungguhnya dari estimator tak bias bagi parameter \(θ\) disebut sebagai efisiensi bagi estimator tersebut dan dinotasikan dengan \(e(\hat{θ})\). Jika \(e(\hat{θ})=1\), maka variansnya minimum yang artinya estimator yang dihasilkan adalah efisien. Akan tetapi, jika \(e(\hat{θ})≠1\), maka varians belum minimum atau estimator belum efisien bagi parameter
Jadi, estimator dikatakan efisien jika estimator tersebut tak bias dan variansnya minimum, yakni ketika varians dari estimator mencapai Batas Bawah Cramer-Rao (CRLB).
Berdasarkan penjelasan kita di atas, untuk menentukan apakah sebuah estimator termasuk estimator yang efisien, kita dapat melakukan beberapa langkah berikut:
- Tentukan apakah estimator yang dihasilkan adalah tak bias, yakni \(E(\hat{θ})=θ\).
- Carilah varians dari estimator, yakni \(Var(\hat{θ})\).
- Tentukan nilai Informasi Fisher, yakni \[ I(θ) = - E \left[ \frac{\partial^2}{\partial θ^2} \ln f(x,θ) \right] \]
- Tentukan nilai Batas Bawah Cramer Rao atau Cramer Rao Lower Bound (CRLB), yakni: \[ CRLB = \frac{ 1 }{n \cdot I(θ)} \]
- Hitung nilai efisiensi bagi \( \hat{θ} \), yakni \[ e(\hat{θ}) = \frac{CRLB}{Var(\hat{θ})} \]
- Kesimpulan: Jika \(e(\hat{θ})=1\), maka varians minimum yang artinya estimator yang dihasilkan adalah efisien. Akan tetapi, jika \(e(\hat{θ})≠1\), maka varians belum minimum atau estimator belum efisien bagi parameter \(θ\).
Contoh 1:
Misalkan \(X_1, …,X_n\) adalah sampel acak independen dari populasi yang berdistribusi Poisson dengan parameter θ, yakni \(X_i \sim Poi(θ)\). Selidikilah apakah \(\overline{X}\) adalah estimator yang efisien bagi \(θ\).
Pembahasan:
Dengan menggunakan metode estimasi maksimum likelihood, kita peroleh \(\hat{θ}_{MLE}=\bar{x}\). Selanjutnya, kita ikuti enam langkah penyelesaian seperti dibahas di atas, yakni:
Langkah 1: Menentukan ketakbiasan estimator

Karena \( E \left( \hat \theta \right) = \theta \), maka \(\hat{θ}_{MLE}=\bar{x}\) adalah estimator tak bias bagi parameter \( \theta \).
Langkah 2: Mencari varians dari estimator

Langkah 3: Mencari nilai informasi Fisher
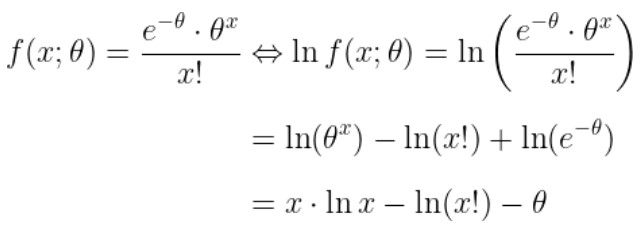

Langkah 4: Menentukan Batas Bawah Cramer Rao (CRLB)

Langkah 5: Hitung nilai efisiensi bagi \(\hat{θ}\)

Langkah 6: Kesimpulan.
Karena \(\hat{θ}=\bar{x}\) adalah estimator tak bias bagi parameter \(θ\) dan varians dari \(\hat{θ}\) mencapai Batas Bawah Cramer Rao yang artinya varians minimum, maka \(\bar{x}\) adalah estimator yang efisien bagi parameter \(θ\).
Contoh 2:
Misalkan \(X_1, …,X_n\) adalah sampel acak independen dari populasi yang berdistribusi Gamma dengan parameter 2 dan \(θ\), yakni \(X_i \sim Gamma(2,θ)\). Selidikilah apakah \(\hat{θ}_{MLE}\) adalah estimator yang efisien bagi \(θ\).
Pembahasan:
Dengan menggunakan metode estimasi maksimum likelihood, kita peroleh penduga MLE bagi parameter \(θ\) yaitu \(\hat{θ}_{MLE} = \bar{x}/2 \). Selanjutnya, sama seperti pada dua contoh di atas, kita akan ikuti 6 langkah penyelesaian, yakni:
Langkah 1: Menentukan ketakbiasan estimator

Karena \( E \left( \hat \theta \right) = \theta \), maka \(\hat{θ}_{MLE}=\bar{x}/2\) adalah estimator tak bias bagi parameter \( \theta \).
Langkah 2: Mencari varians dari estimator

Langkah 3: Mencari nilai informasi Fisher


Langkah 4: Menentukan Batas Bawah Cramer Rao (CRLB)

Langkah 5: Hitung nilai efisiensi bagi \(\hat{θ}\)

Langkah 6: Kesimpulan.
Karena \(\hat{θ}_{MLE} = \bar{x}/2 \) adalah estimator tak bias bagi \(θ\) dan varians dari \(\hat{θ}\) mencapai batas bawah cramer rao (variansnya minimum), maka \(\hat{θ}_{MLE} = \bar{x}/2 \) adalah estimator yang efisien bagi \(θ\).
Cukup sekian penjelasan mengenai estimator atau penduga yang efisien dalam artikel ini. Semoga bermanfaat.
Sumber:
Wackerly, Denis D., Mendenhall III, Wiliam., dan Scheaffer, Richard L. 2008. Mathematical Statistics with Applications. Belmont, CA: Thomson Learning, Inc.
Artikel Terkait
One day you will wake up and there won't be any more time to do the things you've always wanted. Do it now.
Paulo Coelho