
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
STATISTIKA MATEMATIKA II
Statistika Matematika II
Pendugaan Titik
Kriteria Pendugaan yang Ideal
Pendugaan Interval
Statistika Matematika II » Kriteria Estimator yang Ideal › Estimator (Penduga) Konsisten
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552
Consistency
Estimator (Penduga) Konsisten
Estimator yang konsisten artinya apabila ukuran sampel bertambah besar, maka varians estimator tersebut akan semakin kecil dan nilai estimator akan mendekati nilai parameternya.
Salah satu kriteria estimator atau penduga yang ideal bagi parameter populasi adalah kekonsistenan. Estimator yang konsisten artinya apabila ukuran sampel semakin bertambah besar, maka ragam atau varians estimator tersebut akan semakin kecil dan nilai estimator akan semakin mendekati nilai parameternya.
Konsistensi berkaitan dengan sifat asimtotis suatu estimator, yaitu menggambarkan sifat estimator ketika sampel semakin besar (increasing sample size). Untuk menentukan konsistensi suatu estimator, digunakan konsep barisan estimator (sequence estimator).
Untuk memberikan gambaran mengenai sifat estimator yang konsisten ini, perhatikan contoh kasus berikut. Misalkan sebuah koin dilempar sebanyak n kali dan mempunyai peluang sebesar \(p\) jika muncul bagian depan. Jika tiap lemparan bersifat independen, maka \(Y\), yakni jumlah bagian depan yang muncul di antara \(n\) lemparan, akan mengikuti distribusi binomial. Jika nilai sebenarnya dari \(p\) tidak diketahui, proporsi sampel \(Y/n\) merupakan estimator atau penduga bagi \(p\). Lalu apa yang terjadi dengan proporsi sampel ini ketika jumlah lemparan \(n\) meningkat?
Intuisi kita akan menuntun kita untuk percaya bahwa ketika \(n\) bertambah besar, \(Y/n\) seharusnya mendekati nilai \(p\) yang sebenarnya, yakni ketika jumlah informasi dalam sampel meningkat, estimator yang diperoleh seharusnya semakin dekat ke kuantitas parameter yang sedang diestimasi.
Gambar 1 mengilustrasikan sebuah barisan tunggal (single sequence) dari nilai \(\hat{p}=Y/n\) untuk 1000 percobaan Bernoulli ketika nilai \(p\) sebenarnya adalah 0.5. Perhatikan bahwa nilai \(\hat{p}\) memancul di sekitaran 0.5 ketika jumlah percobaan adalah kecil, tetapi mendekati dan sangat dekat dengan \(p = 0.5\) ketika jumlah percobaan meningkat.

Gambar 1. Barisan tunggal nilai \(\hat{p}=Y/n\) untuk 1000 percobaan Bernoulli
Barisan tunggal dari 1000 percobaan sebagaimana diilustrasikan dalam Gambar 1 memberikan nilai estimasi yang sangat mendekati nilai p sebenarnya \((p = 0.5)\) untuk \(n\) yang besar. Pertanyaannya adalah apakah barisan lainnya menunjukkan hasil yang sama? Gambar 2 menunjukkan hasil kombinasi dari 50 barisan berbeda dari nilai \(\hat{p}\) masing-masing dengan 1000 percobaan.
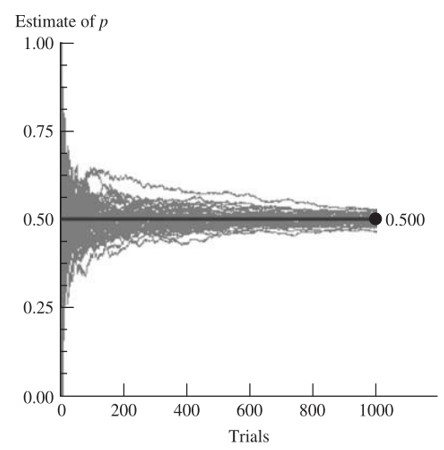
Gambar 2. 50 barisan berbeda dari nilai \(\hat{p}\) untuk 1000 percobaan Bernoulli
Perhatikan bahwa 50 barisan berbeda tersebut adalah tidak identik. Lebih tepatnya, Gambar 2 menunjukkan semacam adanya konvergensi ke nilai \(p\) sebenarnya, yakni \(p = 0.5\). Hal ini ditunjukkan oleh penyebaran nilai estimasi yang lebih luas untuk jumlah percobaan yang lebih kecil, tetapi penyebaran nilai estimasi yang jauh lebih sempit ketika jumlah percobaan lebih besar.
Bagaimana kita bisa secara teknis mengungkapkan jenis "konvergensi" yang ditunjukkan pada Gambar 2? Karena \(Y/n\) merupakan variabel acak, kita dapat menyatakan "kedekatan" ini dengan \(p\) dalam istilah probabilistik. Secara khusus, mari kita periksa probabilitas bahwa jarak antara estimator dan parameter target, \(|(Y/n)-p|\), akan kurang dari sembarang bilangan real positif, yakni
\[ P \left( \left| \frac{Y}{n} - p \right| \right) \leq \varepsilon \]
Gambar 2 tampaknya menunjukkan bahwa peluang ini akan meningkat ketika \(n\) bertambah besar. Jika intuisi kita benar dan \(n\) adalah besar, peluang ini harusnya mendekati 1. Jika peluang ini dalam kenyataannya memang mendekati 1 ketika \(n→∞\), maka kita katakan bahwa \(Y/n\) adalah penduga yang konsisten bagi \(p\), atau bahwa \(Y/n\) “konvergen dalam probabilitas ke \(p\)”.
Kita nyatakan hasil di atas dengan definisi lebih formal berikut. Perhatikan bahwa Kita akan menggunakan notasi \(\hat{θ}_n\) untuk menyatakan barisan estimator yang diperoleh berdasarkan sampel berukuran \(n\). Sebagai contoh, \(\bar{Y}_2\) adalah rata-rata dari dua observasi, sedangkan \(\bar{Y}_{100}\) adalah rata-rata dari 100 observasi. Jadi, ketika membahas sifat konsistensi dari suatu estimator, kita akan selalu menggunakan notasi ini.
Definisi:
Anggap \( \hat{θ}_n \) adalah suatu barisan estimator bagi \(θ\). Estimator tersebut dikatakan sebagai estimator yang konsisten bagi \(θ\) jika untuk sembarang bilangan real positif \((ε>0)\), berlaku:

Ada beberapa konsep penting yang perlu dipahami terkait kekonsistenan estimator, yakni konsep tentang estimator tak bias secara asimtotis (asymptotically unbiased estimator) dan mean square error (MSE).
Definisi: asymptotically unbiased
Sebuah barisan estimator \( \hat{θ}_n \) dikatakan asymptotically unbiased jika \( \lim_\limits{n \to \infty }\, E(\hat{θ}_n) = 0 \) untuk semua \(θ ∈ Ω\).
Dengan kata lain, estimator tak bias secara asimtotis (asymptotically unbiased) adalah estimator yang tak bias ketika ukuran sampel semakin membesar mendekati tak hingga.
Definisi: Konsistensi dalam MSE
Jika \( \hat{θ}_n \) adalah barisan estimator untuk \(θ\), maka \( \hat{θ}_n \) dikatakan konsisten jika mean squared error (MSE) bernilai nol ketika ukuran sampel mendekati tak hingga, yakni

Dengan kata lain, jika kita mengumpulkan pengamatan sampel dalam jumlah besar, kita berharap mendapatkan banyak informasi mengenai parameter yang tak diketahui \(θ\) dan karena itu kita berharap mempunyai estimator dengan MSE yang sangat kecil atau bernilai nol ketika ukuran sampelnya mendekati tak hingga.
Teorema
Sebuah barisan estimator dari \(θ\) adalah konsisten dalam mean squared error jika dan hanya jika tak bias secara asimtotis (asymptotically unbiased) dan \( \lim_\limits{n \to \infty }\, Var(\hat{θ}_n) = 0 \).
Konsistensi dalam MSE berakibat bahwa Bias \( \hat{θ} \) dan varians \( \hat{θ} \) akan mendekati nol. Sehingga dapat dikatakan bahwa \( \hat{θ}_n \) adalah barisan estimator yang konsisten jika

Berdasarkan penjelasan kita di atas, untuk menentukan apakah suatu estimator bersifat konsisten, kita dapat lakukan beberapa langkah berikut:
- Memerika apakah estimator yang dihasilkan merupakan estimator tak bias secara asimtotis, yakni apakah persamaan berikut terpenuhi:
- Memeriksa apakah varians \( \hat{θ}_n \) akan konvergen ke nol untuk \(n\) menuju tak hingga \((n→∞)\), yakni apakah persamaan berikut ini terpenuhi:
\[ \lim_{x\to \infty} E \left( \hat \theta_n \right) = \theta \]
\[ \lim_{x\to \infty} Var \left( \hat \theta_n \right) = 0 \]
Untuk lebih jelasnya, mari kita perhatikan beberapa contoh soal berikut ini.
Contoh 1:
Misalkan \(X_1,…,X_n\) adalah sampel acak bebas (independent random samples) yang berdistribusi Poisson dengan parameter \(θ\), yakni \(X_i \sim POI(θ)\). Apakah \(\bar{X}\) merupakan estimator yang konsisten bagi parameter \(θ\)?
Pembahasan:
Pertama, kita perlu mencari estimator bagi parameter \(θ\). Estimator MLE bagi parameter \(θ\) yaitu \( \hat{θ}_n = \bar{x}_n \).
(Perhatikan bahwa ketika membahas sifat konsistensi suatu estimator, kita menggunakan notasi \( \hat{θ}_n\) untuk menyatakan barisan estimator yang diperoleh berdasarkan sampel berukuran \(n\))
Selanjutnya, kita periksa apakah estimator \( \hat{θ}_n = \bar{x}_n \) adalah asymptotically unbiased.

Dari hasil di atas, diketahui bahwa estimator \( \hat{θ} = \bar{x}_n \) bersifat asymptotically unbiased. Kita lanjutkan dengan memeriksa apakah varians \( \hat{θ} = \bar{x}_n \) akan konvergen ke nol untuk \(n\) menuju tak hingga \((n→∞)\).

Dari hasil di atas diketahui bahwa varians estimator \( \hat{θ}_n = \bar{x}_n \) adalah konvergen ke nol untuk \(n\) menuju tak hingga, yakni \( \lim_\limits{n \to \infty }\, Var(\hat{θ}_n) = 0 \). Dengan demikian, karena \( \hat{θ}_n = \bar{x}_n \) adalah tak bias secara asimtotis dan variansnya konvergen ke nol untuk \(n→∞\), maka \( \hat{θ}_n = \bar{x}_n \) merupakan barisan estimator yang konsisten atau \(\bar{x}_n\) merupakan estimator yang konsisten bagi parameter \(θ\).
Contoh 2:
Misalkan \(X_1,…,X_n\) adalah sampel acak bebas (independent random samples) yang berdistribusi eksponensial dengan parameter \(θ\), yakni \(X_i \sim EXP(θ)\). Selidikilah apakah \( \hat{θ}_{MLE} \) adalah barisan estimator yang konsisten bagi parameter \(θ\)?
Pembahasan:
Pertama, kita perlu mencari estimator bagi parameter \(θ\). Kita peroleh estimator MLE bagi parameter \(θ\), yaitu \( \hat{θ}_n = \bar{x}_n \).
Selanjutnya, kita periksa apakah estimator \( \hat{θ}_n = \bar{x}_n \) adalah asymptotically unbiased.

Dari hasil di atas, diketahui bahwa estimator \( \hat{θ} = \bar{x}_n \) bersifat asymptotically unbiased. Kita lanjutkan dengan memeriksa apakah varians \( \hat{θ} = \bar{x}_n \) akan konvergen ke nol untuk \(n\) menuju tak hingga \((n→∞)\).

Dari hasil di atas diketahui bahwa varians estimator \( \hat{θ} = \bar{x}_n \) adalah konvergen ke nol untuk \(n\) menuju tak hingga, yakni \( \lim_\limits{n \to \infty }\, Var(\hat{θ}_n) = 0 \). Dengan demikian, karena \( \hat{θ}_n = \bar{x}_n \) adalah tak bias secara asimtotis dan variansnya konvergen ke nol untuk \(n→∞\), maka \( \hat{θ}_n = \bar{x}_n \) merupakan barisan estimator yang konsisten atau \(\bar{x}_n\) merupakan estimator yang konsisten bagi parameter \(θ\).
Contoh 3:
Misalkan \(X_1,…,X_n\) adalah sampel acak bebas (independent random samples) dari distribusi dengan fungsi kepadatan peluang (probability density function, pdf) yaitu \(f(x;θ)=1/θ\) jika \(0 < x ≤ θ\) dan \(f(x;θ)=0\) untuk nilai \(x\) yang lainnya. Tunjukkan bahwa estimator yang diperoleh dengan metode momen \(\hat{θ}_{ME}\) merupakan MSE konsisten!
Pembahasan:
Berdasarkan fungsi kepadatan peluang yang diberikan, sampel acak \(X_1,…,X_n\) mempunyai distribusi uniform kontinu. Pertama, kita perlu mencari estimator bagi parameter \(θ\) dengan menggunakan metode momen, yakni
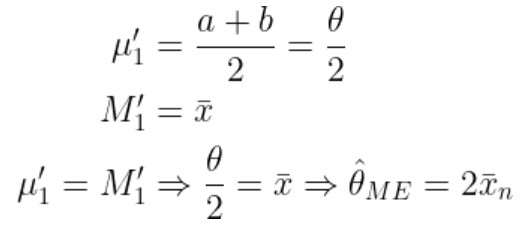
Dari hasil di atas, kita peroleh \(\hat{θ}_n = 2 \bar{x}_n\). Selanjutnya, kita periksa apakah estimator yang diperoleh termasuk asymptotically unbiased.
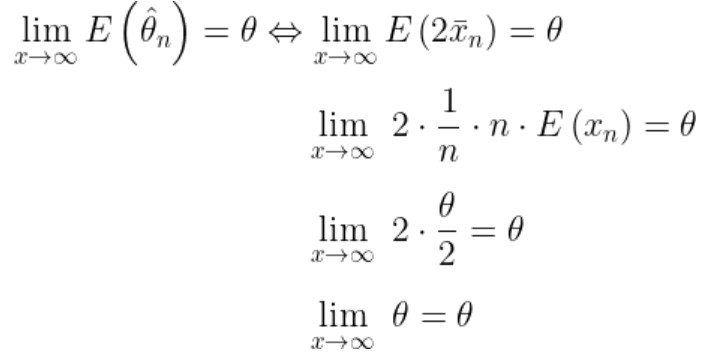
Dari hasil pemeriksaan, ternyata diperoleh bahwa estimator yang dihasilkan adalah asymptotically unbiased. Setelah itu, kita lanjutkan dengan memeriksa apakah varians \( \hat{θ}_n \) konvergen menuju nol untuk \(n\) menuju tak hingga \((n→∞)\).

Ingat bahwa varians dari distribusi uniform kontinu, yaitu:

Dari hasil ini diperoleh bahwa varians estimator yang dihasilkan adalah konvergen ke nol. Dengan demikian, karena telah terbukti bahwa \(\hat{θ}_n = 2 \bar{x}_n\) adalah estimator tak bias secara asimtotis dan \( \lim_\limits{n \to \infty }\, Var(\hat{θ}_n) = 0 \), maka \(\hat{θ}_{ME} = 2 \bar{x}_n\) merupakan barisan estimator yang konsisten atau estimator yang konsisten bagi parameter \(θ\).
Cukup sekian penjelasan mengenai estimator atau penduga yang konsisten dalam artikel ini. Semoga bermanfaat.
Sumber:
Wackerly, Denis D., Mendenhall III, Wiliam., dan Scheaffer, Richard L. 2008. Mathematical Statistics with Applications. Belmont, CA: Thomson Learning, Inc.
Artikel Terkait
One bad chapter does not make the book of your life.
Unknown