Contoh 1:

Misal \(X_1, …,X_n\) adalah sampel acak (random sample) dari populasi yang berdistribusi Poisson dengan parameter \(θ\). Tentukan apakah estimator \(\hat{θ} = \overline{x} \) merupakan estimator yang tak bias bagi \(θ\).

Pembahasan:

Seperti sudah dijelaskan di atas bahwa untuk suatu estimator yang tak bias, maka \(E(\hat{θ})=θ\), sehingga kita peroleh

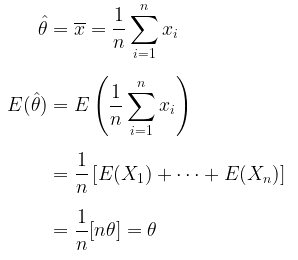
Dengan demikian, karena \(E(\hat{θ})=θ\), maka \(\hat{θ} = \overline{x} \) adalah estimator yang tak bias bagi parameter \(θ\).

Contoh 2:

Misalkan \(X_1, …, X_n\) adalah sampel acak (random sample) dari populasi berdistribusi normal dengan rata-rata \(μ\) dan varians \(σ^2\). Tentukan apakah estimator bagi \(μ\) dan \(σ^2\) adalah estimator yang tak bias?

Pembahasan:

Dari metode momen atau metode maksimum likelihood, diperoleh estimator bagi \(μ\) dan \(σ^2\), yaitu:

\(\bullet\) Memeriksa apakah \(\hat{μ} = \overline{x}\) adalah estimator yang tak bias bagi parameter \(μ\):

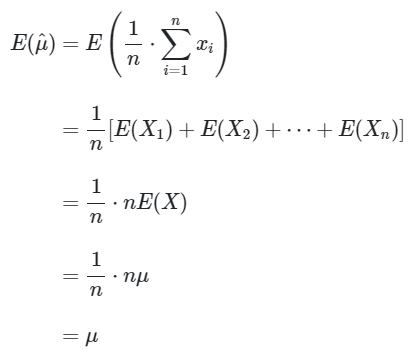
Karena \(E(\hat{μ})=μ\), maka \(\hat{μ} = \overline{x} \) adalah estimator yang tak bias bagi parameter \(μ\).

\(\bullet\) Memeriksa apakah \(\hat{σ}^2 = \frac{\sum_\limits{i=1}^n (x_i-\overline{x})^2}{n}\) adalah estimator yang tak bias bagi parameter \(σ^2\):

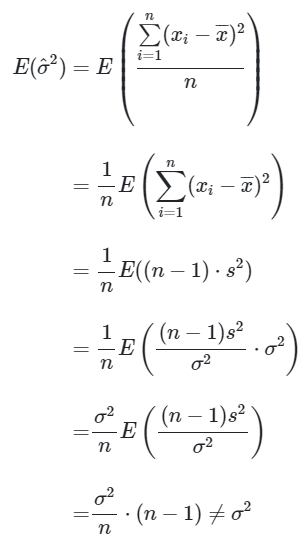
Karena \(E(\hat{σ}^2)≠σ^2\), maka \(\hat{σ}^2\) adalah estimator yang bias bagi \(σ^2\).

Note:

Jika \(X_i \sim χ_v^2\), maka \(E(X)=v\) dan \(V(X)=2v\) sehingga,

Contoh 3:

Misalkan \(X_1, …,X_n\) adalah sampel acak bebas (independent random sample) dari populasi yang berdistribusi uniform, yakni \(X_i \sim Uniform(θ-0,5;θ+0,5)\). Dengan menggunakan metode momen, tentukan estimator bagi parameter \(θ\) dan selidiki apakah estimator tersebut adalah tak bias.

Pembahasan:

Kita cari estimator untuk \( \theta \) terlebih dahulu menggunakan metode momen. Karena random sampel berdistribusi uniform, maka kita peroleh berikut ini.

Selanjutnya, kita periksa apakah estimator yang kita peroleh adalah bias atau tidak.

Karena \( E(\hat{\theta}) = \theta \) maka \( \hat{\theta} = \overline{x} \) merupakan estimator tak bias (unbiased estimator) bagi parameter \( \theta \).

Contoh 4:

Misalkan \(X_1, …,X_n\) adalah sampek acak bebas dari populasi berdistribusi geometrik \(Geo(θ); \ i =1,2,...,n\). Periksalah apakah \(\hat{θ} = 1/\overline{x}\) adalah estimator tak bias bagi parameter \( θ \).

Pembahasan:

Seperti sudah dijelaskan di atas bahwa untuk suatu estimator yang tak bias, maka \(E(\hat{θ})=θ\), sehingga kita peroleh

Karena \( E(\hat{\theta}) = \theta \), maka \( \hat{\theta} = 1/\overline{x} \) merupakan estimator tak bias (unbiased estimator) bagi parameter \( \theta \).