
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
STATISTIKA NONPARAMETRIK
Statistik Nonparametrik
Pendahuluan
Kasus Satu Sampel
Kasus Dua Sampel Independen
Kasus Dua Sampel Berhubungan
Kasus Banyak Sampel Independen
Kasus Banyak Sampel Berhubungan
Koefisien Korelasi (Korelasi Nonparametrik)
Statistik Nonparametrik » Kasus Dua Sampel Berhubungan › Uji McNemar - Rumus dan Contoh Penghitungan
Uji McNemar
Uji McNemar - Rumus dan Contoh Penghitungan
Uji McNemar digunakan untuk menguji perbedaan proporsi dua populasi yang berhubungan (dependen) yang mana hanya memiliki dua kategori.
Uji McNemar digunakan untuk menguji perbedaan atau perubahan proporsi dua populasi yang berhubungan yang mana hanya memiliki dua kategori. Uji ini banyak dipakai untuk mengetahui apakah terdapat perbedaan proporsi sebelum dan sesudah kelompok sampel tertentu diberi perlakuan, di mana anggota kelompok sampel tersebut merupakan kontrol terhadap dirinya sendiri.
Uji McNemar menggunakan data dengan skala pengukuran nominal atau dikotomi. Dengan demikian, uji ini dapat dipakai untuk menguji keefektifan suatu perlakuan tertentu (misalnya: kampanye, pertemuan, brosur, iklan) terhadap kecenderungan pilihan para subjek atas berbagai pilihan.
Untuk menguji perubahan yang signifikan dari setiap subjek yang diobservasi dengan metode ini, maka dibentuk suatu tabel frekuensi yang berbentuk segi empat. Di sini ditunjukkan kelompok jawaban pertama dan kedua dari orang yang sama.
Tabel 1. Tampilan data hasil observasi atau pengamatan
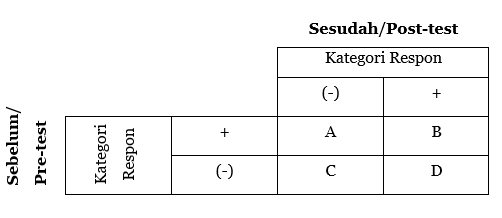
Tanda “-“ dan “+” dipakai untuk menandai kategori respon (jawaban) yang berbeda. Jadi tidak harus bersifat positif dan negatif yang sesungguhnya. Kasus-kasus yang menunjukkan perubahan antara jawaban pertama dan kedua muncul dalam sel A dan D.
Seseorang dicatat dalam sel A jika berubah dari kategori respon “+” menjadi kategori respon “-“ dan dicatat pada sel D jika berubah dari kategori respon “-“ menjadi kategori respon “+”. Sementara itu, jika tidak ada perubahan kategori respon “+” yang diobservasi, maka dicatat di sel B. Jika tidak ada perubahan kategori respon “-“ yang diobservasi, dicatat di sel C. Sel (A+D) adalah jumlah total orang/subjek yang berubah, sel B dan C adalah yang tidak berubah.
Hipotesis nol \( (H_0) \) Uji McNemar menyatakan bahwa jumlah perubahan pada setiap kategori respon adalah sama, yakni dari jumlah \(A+D\) yang berubah, diharapkan ((A+D))/2 individu berubah dari kategori respon “+” ke kategori respon “-“ dan ((A+D))/2 individu berubah dari kategori respon “-“ ke kategori respon “+”. Dengan kata lain, jika \(H_0\) benar, frekuensi yang diharapkan pada sel A dan D adalah ((A+D))/2.
Rumus Uji McNemar
Pada Uji McNemar yang diperhatikan hanya subjek-subjek yang berubah yaitu hanya sel A dan sel D. Distribusi sampling untuk uji ini adalah chi-square, dengan koreksi kontinuitas. Rumus yang digunakan, yaitu:
\[ \chi^2_{hit} = \frac{ \left( |A-D|-1 \right)^2 }{A + D} \]
Statistik hitung \( \chi^2_{hit} \) akan mengikuti distribusi chi-square dengan derajat bebas 1.
Prosedur Penghitungan Uji McNemar
- Tentukan Hipotesis Nol \((H_0)\) dan Hipotesis Alternatif \((H_1)\).
- Tentukan Taraf signifikansinya \((α)\)
- Hitunglah statistik ujinya dengan cara:
- Masukkan frekuensi yang teramati ke dalam tabel berukuran \(2 \times 2\) seperti yang diberikan di atas.
- Tentukan jumlah total dari “perubahan” (A + D). Jika jumlah total perubahan kurang dari 10, lebih baik gunakan uji binomial dibandingkan Uji McNemar. Apabila \( \frac{A+D}{2} < 5\), uji yang dipakai adalah uji binomial dengan \(n = A + D\), dan \(x\) = nilai yang terkecil antara A dan D. Apabila \( \frac{A+D}{2} \geq 5\), hitung nilai \(χ^2\) menggunakan rumus McNemar yang diberikan di atas.
- Wilayah kritis: Tolak \(H_0\) jika \(χ^2 ≥ χ^2 (α,(k-1))\) atau \(p-value ≤ α\).
- Tentukan keputusan berdasarkan daerah kritis.
- Kesimpulan.
Contoh Soal 1:
Pada bulan April 2016 dilakukan survei di Desa Sukamaju, rumah-rumah yang ada di suatu RT dinilai dalam kategori kotor (-) dan bersih (+). Bulan Mei diadakan penyuluhan tentang pentingnya kebersihan rumah dan halaman. Sebulan kemudian dilakukan lagi penilaian seperti bulan April, yaitu kategori kotor dan bersih. Kemudian dihitung perubahan-perubahan yang terjadi pada rumah-rumah di RT tersebut, dengan hasil sebagai berikut:

Dengan taraf nyata sebesar alpha = 5% , apakah ada perbedaan perilaku yang signifikan setelah penyuluhan tentang pentingnya kebersihan rumah dan halaman?
Pembahasan:
Karena desainnya bertipe dua sampel berhubungan dan datanya berskala nominal dengan dua kategori (bersih dan kotor), serta bertujuan untuk menguji perbedaan proporsi populasi, maka uji yang dipilih adalah uji McNemar.
Hipotesis: \(H_0\): Peluang untuk berubah menjadi bersih dan kotor sama \((P_A=P_D)\). \(H_1\): Peluang untuk berubah menjadi bersih dan kotor tidak sama \((P_A ≠ P_D)\).
Tingkat signifikansi: alpha = 5%
Uji statistik:
Dalam kasus ini besarnya sampel \(n = 25\), banyaknya orang yang berubah sikap dari ‘kotor’ ke’bersih’ sebanyak 14 orang dan yang berubah sikap dari ‘bersih’ ke ‘kotor’ sebanyak 4 orang. Sebanyak 3 orang tidak berubah sikap tetap ‘bersih’, sedangkan 4 orang tidak berubah sikap tetap ‘kotor’.
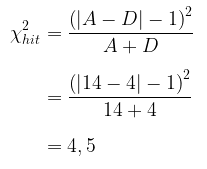
Wilayah kritis: Dari tabel chi-square, diperoleh daerah kritis untuk taraf nyata 0,05 dengan db = 1 adalah 3,84.
Keputusan: Karena nilai \( χ_{hit}^2 = 4,5 > χ^2 (db,α) = 3,84 \), maka tolak \(H_0\).
Kesimpulan: Berdasarkan data sampel yang ada dan dengan tingkat signifikansi 5%, dapat disimpulkan bahwa terdapat cukup bukti untuk menyatakan ada perbedaan yang nyata antara proporsi perilaku hidup bersih sebelum dan sesudah penyuluhan. Dengan kata lain, dapat dikatakan bahwa penyuluhan yang dilakukan cukup efektif.
Contoh Soal 2:
Untuk memilih seorang supervisor (pengawas) yang baru, yang akan memimpin para pekerja pembuat Roti, maka kepada 14 wakil pekerja diberi kesempatan untuk menilai calon supervisor yang bernama AMIR. Dari penilaian yang hanya mempunyai DUA pilihan yaitu SUKA atau TIDAK SUKA, didapat 6 orang suka (setuju) untuk memilih AMIR, sedangkan 8 pekerja tidak suka.
Kemudian Manajer SDM memberi kesempatan kepada AMIR untuk berdialog dengan keempat belas wakil pekerja tadi, termasuk rencana-rencananya seandainya ia didukung menjadi supervisor. Setelah terjadi dialog dan komunikasi dua arah, sekarang Manajer SDM sekali lagi meminta kepada empat belas orang yang sama untuk memberikan penilaian mereka terhadap AMIR.
Dari empat belas karyawan, bisa terdapat pergeseran, yang sebelum berdialog merasa tidak suka, sekarang setelah mengenal dan berdiskusi dengan AMIR menjadi bersikap positif. Namun, ada juga yang berpikiran sebaliknya atau tetap pada pendirian semula.
Berikut hasil penilaian karyawan sebelum diadakan dialog dan setelah diadakan dialog dengan AMIR.
| Nama Pekerja | Sebelum Dialog | Sesudah Dialog |
|---|---|---|
| SUSY | Suka | Tidak Suka |
| RUDY | Suka | Tidak Suka |
| BUDY | Suka | Suka |
| RONNY | Suka | Suka |
| SANNY | Suka | Tidak Suka |
| SANTY | Suka | Tidak Suka |
| TUTY | Tidak Suka | Suka |
| YATY | Tidak Suka | Suka |
| RICKY | Tidak Suka | Suka |
| DICKY | Tidak Suka | Tidak Suka |
| VICKY | Tidak Suka | Suka |
| ELLY | Tidak Suka | Suka |
| LILY | Tidak Suka | Suka |
| LANNY | Tidak Suka | Suka |
Penjelasan data:
- Input berupa data kode: 1 = Suka dan 2 = Tidak Suka
- Data baris pertama: pekerja bernama Susy sebelum dialog merasa suka atau setuju terhadap pengangkatan Amir, namun setelah dialog menjadi tidak suka terhadap Amir. Demikian seterusnya untuk data yang lain.
Pembahasan:
Oleh karena 14 data di atas dianggap tidak berdistribusi normal, serta jumlah sampel di bawah 30, maka digunakan uji nonparametrik. Karena desainnya bertipe dua sampel berhubungan dan datanya berskala nominal dengan dua kategori (suka dan tidak suka), serta bertujuan untuk menguji perbedaan proporsi populasi, maka uji yang dipilih adalah uji McNemar.
Hipotesis: \(H_0\): Peluang untuk berubah menjadi suka dan tidak suka sama \((P_A=P_D)\). \(H_1\): Peluang untuk berubah menjadi suka dan tidak suka adalah tidak sama \((P_A ≠ P_D)\).
Tingkat signifikansi: alpha = 5%
Uji statistik:
Dalam kasus ini besarnya sampel \(n = 14\), banyaknya orang yang berubah sikap dari ‘suka’ ke ’tidak suka’ sebanyak 4 orang dan yang berubah sikap dari ‘tidak suka’ ke ‘suka’ sebanyak 7 orang. Sebanyak 2 orang tidak berubah sikap yakni tetap ‘suka’, sedangkan 1 orang tidak berubah sikap yakni tetap ‘tidak suka’.


Wilayah kritis: Dari tabel chi-square, diperoleh daerah kritis untuk taraf nyata 0,05 dengan db = 1 adalah 3,84.
Keputusan: Karena nilai \( χ_{hit}^2 = 3,63 < χ^2 (db,α) = 3,84 \), maka gagal tolak \(H_0\).
Kesimpulan: Berdasarkan data sampel yang ada dan dengan tingkat signifikansi 5%, dapat disimpulkan bahwa terdapat cukup bukti untuk menyatakan bahwa tidak ada perbedaan yang nyata antara proporsi sikap para pekerja sebelum dan sesudah dialog. Dengan kata lain, dapat dikatakan bahwa kegiatan dialog tidak cukup efektif untuk mengubah sikap para pekerja.
Sumber:
Siegel, Sidney. 1997. Statistika Nonparametrik untuk Ilmu-ilmu Sosial. Jakarta: PT Gramedia Pustaka Utama
Santoso, Singgih. 2018. Menguasai SPSS Versi 25. Jakarta: PT Elex Media Komputindo.
Artikel Terkait
It always seems impossible until it's done.
Nelson Mandela