Statistik Nonparametrik   »   Koefisien Korelasi Nonparametrik   ›  Korelasi Kendall Tau - Rumus dan Contoh Penghitungan

Korelasi Kendall Tau

Korelasi Kendall Tau - Rumus dan Contoh Penghitungan

Korelasi kendall tau digunakan untuk mengukur tingkat kesesuaian yakni apakah ada perbedaan tingkat kesesuaian ranking antara 2 variabel yang diamati.

---

Korelasi Kendall Tau merupakan statistik nonparametrik dengan skala pengukuran data sekurang-kurangnya berskala ordinal. Korelasi kendall tau digunakan untuk mengukur tingkat kesesuaian yakni apakah ada perbedaan tingkat kesesuaian ranking antara 2 variabel yang diamati.

Metodologi

Rumus yang digunakan untuk mengukur koefisien korelasi kendall tau adalah:

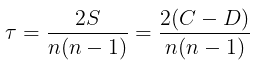
Jika ada ranking yang sama, maka rumus di atas dilengkapi dengan faktor koreksi rank yang sama, yaitu:

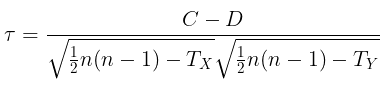
di mana:

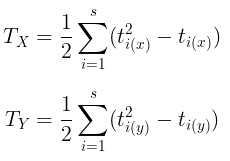
atau secara ekivalen:

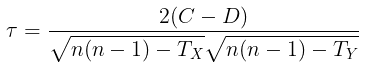
di mana:

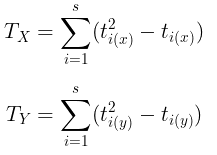
Keterangan:

S: statistik untuk jumlah konkordansi dan diskordansi

C: banyaknya pasangan konkordansi (wajar)

D: banyaknya pasangan diskordansi (tidak wajar)

n: jumlah pasangan X dan Y

Tx : faktor koreksi ranking X yang sama

Ty : faktor koreksi ranking Y yang sama

Sampel Besar

Jika sampel berukuran lebih dari 10, maka terapkan aproksimasi sampel besar dengan menganggap bahwa distribusi sampel mendekati distribusi normal (z). Dengan demikian, kaidah pengambilan keputusan untuk analisis korelasi kendall tau sebagai berikut:

1. Hipotesis dua arah: tolak Ho jika Z hitung > Z tabel atau Z hitung ≤ -Z tabel untuk n dan tingkat signifikansi α.
2. Hipotesis satu sisi: tolak Ho jika nilai Z hitung > nilai Z tabel untuk n dan tingkat signifikansi α.
3. Hipotesis satu sisi: tolak Ho jika nilai Z hitung < -Z tabel untuk n dan tingkat signifikansi α.

Statistik uji untuk sampel besar yaitu:

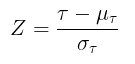
di mana:

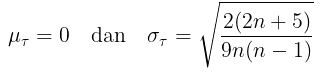
Prosedur Uji Signifikansi Korelasi Kendall Tau

Adapun langkah-langkah perhitungan koefisien korelasi kendall tau yaitu:

1. Tentukan hipotesis nol dan hipotesis alternatif. \(H_0\): tidak ada kesesuaian ranking yang diberikan oleh \(X\) dan \(Y\) dalam populasi. \(H_1\): ada kesesuaian ranking yang diberikan oleh \(X\) dan \(Y\) dalam populasi.
2. Tentukan tingkat signifikansi \(α\).
3. Hitung statistik uji dengan cara:
   • Susunlah pasangan-pasangan (\(X_i\) dan \(Y_i\)) dalam kolom menurut besarnya nilai-nilai \(X\), dari nilai \(X\) yang paling kecil, dalam hal ini nilai-nilai \(X\) berada dalam urutan yang wajar (natural order).
   • Bandingkan setiap nilai \(Y\), satu demi satu dengan nilai yang ada di sebelah kanannya, bila urutannya wajar (concordan) beri nilai 1, sedangkan bila urutannya tidak wajar (disconcordan) beri nilai -1 (kurang 1).
   • Tentukan jumlah Concordan (\(C\)) dan Disconcordan (\(D\)).
   • Hitung nilai \(S\) yang diperoleh dari \(C – D\).
   • Hitung nilai statistik \(τ\).
4. Wilayah kritis:
5. Buatlah keputusan terima atau tolak Ho berdasarkan wilayah kritisnya.
6. Kesimpulan:

Contoh Soal 1:

Diketahui sebuah ranking nilai wawancara dari dua orang pewawancara kepada 10 orang peserta dari tes tertulis dan tes praktek. Data nilai ranking sebagai berikut:

Apakah ada hubungan ranking penilaian dari pewawancara 1 dan pewawancara 2? Gunakan tingkat signifikansi 5%.

Pembahasan:

Hipotesis:

H0: Tidak ada kesesuaian ranking nilai pewawancara 1 dan pewawancara 2

H1: Ada kesesuaian ranking nilai pewawancara 1 dan pewawancara 2

Tingkat signifikansi (alpha = 0,05)

Statistik uji

Ranking berdasarkan urutan pewawancara 1

Sesudah mengatur ranking-ranking itu, dengan dasar ranking dari pewawancara 1, kita tetapkan harga S untuk ranking yang saling berhubungan dengan variabel Y sehingga diperoleh nilai S sebesar 25.

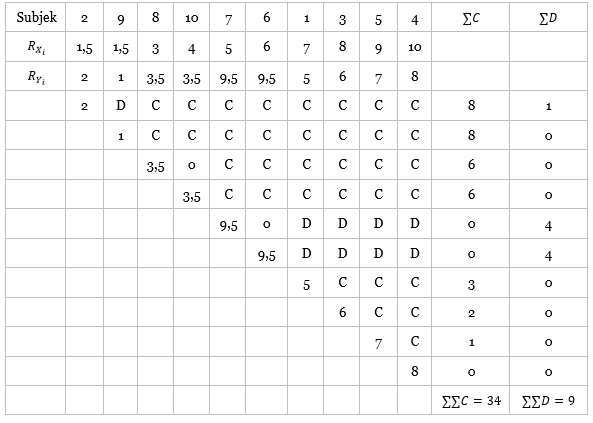
Karena terdapat ranking kembar, maka gunakan rumus korelasi kendall tau dengan faktor koreksi. Pertama kita hitung dulu yang berikut ini.

Dengan demikian, kita peroleh

Pada tabel kendall tau untuk nilai S = 25 dan n = 10 diperoleh nilai τ tabel = 0,014. Karena nilai τ hitung > τ tabel, maka tolak Ho pada tingkat signifikansi α=5%.

Kesimpulan: Dengan tingkat signifikansi 5%, terdapat cukup bukti untuk mengatakan bahwa ada kesesuaian ranking nilai pewawancara 1 dan pewawancara 2 di tingkat populasi.

Contoh Soal 2:

Dalam sebuah penelitian ingin diketahui apakah nilai matakuliah statistik teori mempunyai hubungan dengan nilai matakuliah statistik praktek. Peneliti mengambil sampel sebanyak 12 orang mahasiswa secara acak dan diperoleh hasil sebagai berikut:

Apakah ada hubungan nilai mata kuliah statistik teori dan nilai matakuliah statistik praktek? Gunakan tingkat signifikansi 1%.

Pembahasan:

Hipotesis:

H0: tidak ada kesesuaian ranking skor hasil belajar statistik teori dan praktik mahasiswa di tingkat populasi.

H1: ada kesesuaian ranking skor hasil belajar statistik teori dan praktik mahasiswa di tingkat populasi.

Tingkat signifikansi (alpha = 0,01)

Statistik uji:

Ranking berdasarkan urutan mahasiswa:

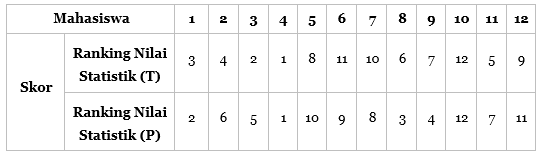
Urutan berdasarkan peringkat nilai statistik

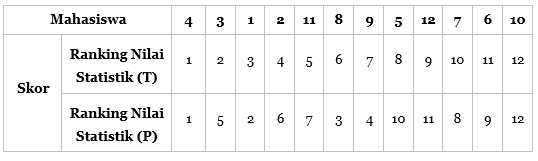
Sesudah mengatur ranking-rangking itu, variabel X dalam urutan yang wajar, kita tetapkan harga S untuk ranking yang saling berhubungan dengan variabel Y;

Ranking nilai statistik praktek yang paling kiri adalah ranking 1, ini memiliki 11 ranking yang lebih besar sebelah kanannya dan 0 ranking yang lebih kecil di sebelah kirinya, jadi skornya (11-0), begitu seterusnya sehingga didapat harga S = 44.

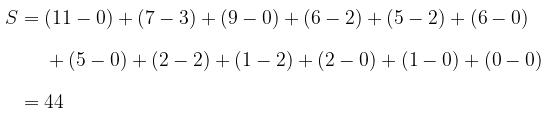
Dengan demikian, korelasi atau tingkat hubungan antara mata kuliah statistik teori dan praktek adalah

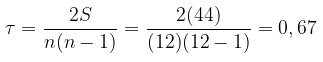
Karena n > 10, maka kita dapat gunakan pendekatan sampel besar. Kita hitung statistik Z, yakni

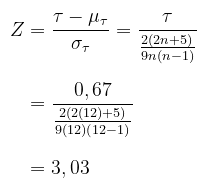
Keputusan: Dengan melihat tabel nilai-nilai z, kita mengetahui bahwa z > 3,03 mempunyai kemungkinan kemunculan, di bawah H0, sebesar p = 0,0012. Dengan demikian, kita dapat menolak H0 pada tingkat signifikansi alpha =0,01.

Kesimpulan: Dengan tingkat sigifikansi 1%, cukup bukti untuk mengatakan ada hubungan antara nilai mata kuliah statistik teori dengan nilai mata kuliah statistik praktek.

Sumber:

Siegel, Sidney. 1997. Statistika Nonparametrik untuk Ilmu-ilmu Sosial. Jakarta: PT Gramedia Pustaka Utama