Statistik Nonparametrik   »   Kasus Banyak Sampel Independen   ›  Uji Chi-Square k Sampel Independen- Rumus dan Contoh Penghitungan

Uji Chi-Square

Uji Chi-Square k Sampel Independen- Rumus dan Contoh Penghitungan

Uji Chi-SQuare bertujuan untuk mengetahui apakah ada perbedaan yang signifikan antara frekuensi pengamatan pada tiap kategori atau klasifikasi terhadap nilai yang diharapkan.

---

Oleh Tju Ji Long · Statistisi

Hub. WA: 0812-5632-4552

Uji Chi-square digunakan untuk membandingkan distribusi hasil observasi (pengamatan) dengan distribusi yang diharapkan. Uji ini bertujuan untuk mengetahui apakah ada perbedaan yang signifikan antara frekuensi pengamatan pada tiap kategori atau klasifikasi terhadap nilai yang diharapkan.

Metodologi

Dalam distribusi chi-square, nilai frekuensi yang diharapkan untuk setiap sel adalah sama, sampel diukur dengan skala nominal. Dari \(k\) kelompok sampel independen yang masing-masing berukuran \(n_1, n_2,…,n_k\) ingin diketahui apakah ada perbedaan yang signifikan antara frekuensi pengamatan (hasil observasi) pada tiap kategori atau klasifikasi terhadap nilai yang diharapkan.

Hasil observasi dari sebanyak \(k\) sampel dapat ditampilkan dalam tabel sebagai berikut.

Tabel 1. Tampilan data hasil observasi atau pengamatan

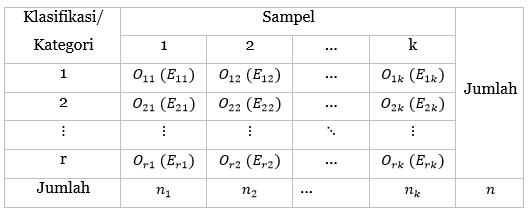
Keterangan:

\(O_{11}\) = hasil observasi yang menunjukkan banyaknya/frekuensi subyek dari kelompok sampel 1 pada kategori 1.

\(E_{11}\) = nilai/frekuensi kelompok sampel 1 yang diharapkan pada kategori 1

Contoh cara menghitung nilai harapan untuk masing-masing sel:

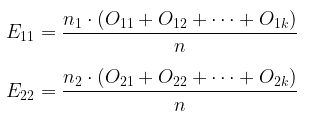
Rumus yang dipakai untuk statistik Uji Chi-Square \(k\) sampel independen adalah:

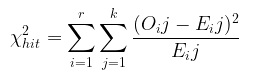
di mana:

\(O_{ij}\) = banyaknya/frekuensi hasil observasi pada baris \(i\) kolom \(j\)

\(E_{ij}\) = nilai/frekuensi yang diharapkan pada baris \(i\) kolom \(j\)

\(i\) = banyaknya baris 1 s/d \(r\)

\(j\) = banyaknya kolom 1 sd \(k\)

Prosedur Uji Chi-Square

Berikut adalah prosedur untuk melakukan uji chi-square.

1. Tentukan hipotesis nol ( \( H_0 \) ) dan hipotesis alternatif ( \( H_1 \) )
2. Tentukan tingkat signifikansi yang digunakan \((α)\)
3. Hitung statistik uji \(χ_{hit}^2\) dengan menggunakan formula berikut.

4. Tentukan wilayah kritis. Lihat nilai \(χ^2\) tabel pada tabel chi-square dengan derajat bebas \((db) = (k-1)(r-1)\); dari tabel tersebut akan diperoleh besarnya nilai-nilai kritis \(χ^2\) tabel.
5. Keputusan: Jika \(p-value ≤ α\), maka tolak \( H_0 \) atau bisa juga membandingkan nilai \(χ^2\) hitung dengan \(χ^2\) tabel yakni jika \(χ^2\) hitung \(≥ χ^2\) tabel maka tolak \( H_0 \).
6. Buatlah kesimpulan dari hasil yang diperoleh.

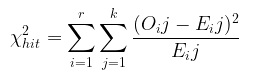
Contoh Soal 1:

Seorang peneliti ingin mengetahui proporsi asal daerah mahasiswa di sebuah perguruan tinggi berdasarkan angkatan masuk mahasiswa ketika masuk ke perguruan tinggi tersebut. Dengan \(α=5 \%\), hitunglah apakah proporsi mahasiswa dari 5 daerah (Jawa, Sumatera, Kalimantan, Sulawesi, dan Papua) adalah sama untuk tiap angkatan? Berikut adalah datanya:

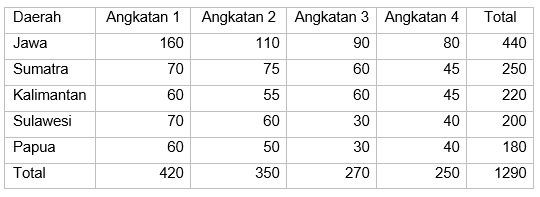
Pembahasan:

Tentukan hipotesis penelitian: \(H_0\): Proporsi mahasiswa dari 5 daerah adalah sama untuk tiap angkatan. \(H_1\): Proporsi mahasiswa dari 5 daerah adalah berbeda untuk tiap angkatan.

Tentukan tingkat signifikansi: Di sini digunakan alpha = 5% = 0,05.

Menghitung statistik uji:

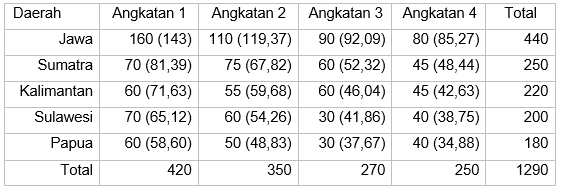
Tentukan wilayah kritis: Tolak \(H_0\) jika \(χ^2\) hitung ≥ \(χ^2\) tabel.

Keputusan: Karena \(χ^2\) hitung lebih kecil dari \(χ^2\) tabel yakni \(20,52 < 21,03\) maka gagal tolak \(H_0\).

Kesimpulan: Dengan tingkat kepercayaan 95% dan berdasarkan sampel yang ada, dapat disimpulkan bahwa tidak terdapat cukup bukti untuk menyatakan proporsi mahasiswa dari 5 daerah (Jawa, Sumatera, Kalimantan, Sulawesi, Papua) adalah berbeda untuk tiap angkatan.

Sumber:

Siegel, Sidney. 1997. Statistika Nonparametrik untuk Ilmu-ilmu Sosial. Jakarta: PT Gramedia Pustaka Utama