
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
STATISTIKA NONPARAMETRIK
Statistik Nonparametrik
Pendahuluan
Kasus Satu Sampel
Kasus Dua Sampel Independen
Kasus Dua Sampel Berhubungan
Kasus Banyak Sampel Independen
Kasus Banyak Sampel Berhubungan
Koefisien Korelasi (Korelasi Nonparametrik)
Statistik Nonparametrik » Koefisien Korelasi Nonparametrik › Koefisien Korelasi Spearman - Rumus dan Contoh Penghitungan
Korelasi Spearman
Koefisien Korelasi Spearman - Rumus dan Contoh Penghitungan
Koefisien korelasi Spearman (Spearman Rank Correlation Coefficient), digunakan untuk menghitung korelasi berdasarkan data yang berbentuk peringkat (ranking).
Koefisien korelasi Spearman atau sering disebut juga sebagai Spearman Rank Correlation Coefficient, digunakan untuk menghitung korelasi berdasarkan data yang berbentuk peringkat (ranking). Berdasarkan kondisi dalam data, terdapat dua cara dalam penghitungan koefisien korelasi Spearman, yaitu:
- Apabila tidak terdapat peringkat yang “kembar/sama” (“tied rank”).
- Apabila terdapat peringkat yang “kembar/sama” (“tied rank”).
Rumus yang digunakan untuk menghitung korelasi Spearman tanpa peringkat sama, yaitu:

Rumus yang digunakan jika terdapat ranking kembar, yaitu:

Keterangan:

Contoh Soal 1:
Sebuah perusahaan sedang melakukan rekrutmen pegawai. Pimpinan perusahaan ingin mengetahui apakah ada hubungan antara nilai ujian tertulis dengan jumlah barang yang dijual oleh masing-masing salesman yang baru direkrut tersebut. Di bawah ini adalah data mengenai ranking nilai ujian tertulis dan ranking hasil penjualan dari sampel 10 orang salesman yang baru direkrut.
| Salesman | Ranking Nilai Ujian Tertulis | Ranking Jumlah Penjualan |
|---|---|---|
| A | 5 | 3 |
| B | 6 | 7 |
| C | 8 | 5 |
| D | 3 | 1 |
| E | 2 | 6 |
| F | 7 | 8 |
| G | 1 | 2 |
| H | 4 | 9 |
| I | 10 | 4 |
| J | 9 | 10 |
Pembahasan:
Hipotesis:
\(H_0\): Tidak ada hubungan antara ranking nilai ujian tertulis salesman dengan rangking jumlah penjualan oleh salesman di tingkat populasi
\(H_1\): Ada hubungan antara ranking nilai ujian tertulis salesman dengan rangking jumlah penjualan oleh salesman di tingkat populasi
Tingkat Signifikansi: \(\alpha = 5\%\)
Statistik uji:
Data yang sudah di ranking.
| Salesman | Ranking Nilai Ujian Tertulis | Ranking Jumlah Penjualan | \(d_i\) | \(d_i^2\) |
|---|---|---|---|---|
| A | 5 | 3 | 2 | 4 |
| B | 6 | 7 | -1 | 1 |
| C | 8 | 5 | 3 | 9 |
| D | 3 | 1 | 2 | 4 |
| E | 2 | 6 | -4 | 16 |
| F | 7 | 8 | -1 | 1 |
| G | 1 | 2 | -1 | 1 |
| H | 4 | 9 | -5 | 25 |
| I | 10 | 4 | 6 | 36 |
| J | 9 | 10 | -1 | 1 |
| \(\sum = 98 \) |
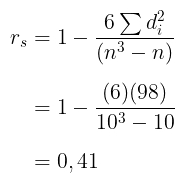
Kemudian, dari tabel korelasi Spearman diperoleh nilai \(r_s (0,05;10)=0,648\).
Keputusan: Karena \(r_s\) hit < \(r_s\) tabel (0,41 < 0,648) maka diputuskan gagal tolak \(H_0\).
Kesimpulan: Dengan tingkat signifikansi 5%, belum cukup bukti untuk mengatakan terdapat hubungan/keterkaitan ranking nilai ujian tertulis dengan ranking jumlah penjualan.
Contoh Soal 2:
Sebuah penelitian dilakukan untuk mengetahui apakah pemahaman siswa terhadap mata pelajaran Matematika dan mata pelajaran Fisika memiliki hubungan atau tidak. Peneliti melakukan penelitian pada 10 siswa SMA untuk mengetahui hubungan tersebut. Sepuluh siswa ini didata nilai ujian untuk mata pelajaran Fisika dan Matematika. Data yang diperoleh adalah sebagai berikut:
| Mahasiswa | A | B | C | D | E | F | G | H | I | J |
|---|---|---|---|---|---|---|---|---|---|---|
| Nilai Matematika | 90 | 87 | 90 | 83 | 83 | 75 | 78 | 85 | 85 | 85 |
| Nilai Fisika | 83 | 80 | 86 | 83 | 75 | 65 | 68 | 80 | 70 | 75 |
Berdasarkan data di atas, ujilah apakah ada hubungan antara pemahaman siswa terhadap mata pelajaran Matematika dan mata pelajaran Fisika? Ujilah dengan tingkat signifikansi 5%.
Pembahasan:
Hipotesis:
\(H_0\): Tidak ada hubungan antara pemahaman siswa terhadap mata pelajaran matematika dan mata pelajran fisika di tingkat populasi.
\(H_1\): Ada hubungan antara pemahaman siswa terhadap mata pelajaran matematika dan mata pelajaran fisika di tingkat populasi.
Tingkat Signifikansi: \(\alpha = 5\%\)
Statistik uji:
Data yang sudah di ranking.
| Mahasiswa | Rank Nilai Matematik | Rank Nilai Fisika | \(d_i\) | \(d_i^2\) |
|---|---|---|---|---|
| A | 2,5 | 1,5 | 1 | 1 |
| B | 4,5 | 3 | 1,5 | 2,25 |
| C | 1 | 1,5 | -0,5 | 0,25 |
| D | 2,5 | 7,5 | -5 | 25 |
| E | 6,5 | 7,5 | -1 | 1 |
| F | 10 | 10 | 0 | 0 |
| G | 9 | 9 | 0 | 0 |
| H | 4,5 | 5 | -0,5 | 0,25 |
| I | 8 | 5 | 3 | 9 |
| J | 6,5 | 5 | 1,5 | 2,25 |
| \(\sum = 41 \) |
Karena terdapat ranking yang kembar, maka kita gunakan rumus penghitungan korelasi Spearman dengan kondisi terdapat rank kembar. Berikut hasil yang diperoleh:



Kemudian, dari tabel korelasi Spearman diperoleh nilai \(r_s (0,05;10)=0,648\).
Keputusan: Karena \(r_s\) hit > \(r_s\) tabel (0,744 > 0,648) maka diputuskan tolak \(H_0\).
Kesimpulan: Dengan tingkat signifikansi 5%, cukup bukti untuk mengatakan ada hubungan antara pemahaman siswa mata pelajaran matematika dan mata pelajaran fisika di tingkat populasi.
Sumber:
Siegel, Sidney. 1997. Statistika Nonparametrik untuk Ilmu-ilmu Sosial. Jakarta: PT Gramedia Pustaka Utama
Artikel Terkait
Don't let yesterday take up too much of today.
Will Rogers