
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
STATISTIKA NONPARAMETRIK
Statistik Nonparametrik
Pendahuluan
Kasus Satu Sampel
Kasus Dua Sampel Independen
Kasus Dua Sampel Berhubungan
Kasus Banyak Sampel Independen
Kasus Banyak Sampel Berhubungan
Koefisien Korelasi (Korelasi Nonparametrik)
Statistik Nonparametrik » Kasus Banyak Sampel Berhubungan › Uji Cochran Q - Rumus dan Contoh Penghitungan
Uji Cochran Q
Uji Cochran Q - Rumus dan Contoh Penghitungan
Uji Cochran Q merupakan perluasan dari Uji McNemar dan digunakan untuk menguji apakah tiga atau lebih sampel berbeda signifikan dalam hal proporsi atau frekuensinya.
Uji Cochran Q merupakan perluasan dari Uji McNemar dan digunakan untuk menguji apakah tiga atau lebih sampel berbeda signifikan dalam hal proporsi atau frekuensinya. Uji ini menggunakan data minimal berskala nominal yang bersifat dikotomi atau hanya terdapat dua kategori, misalnya sukses atau gagal.
Metodologi
Data terdiri atas reaksi-reaksi dari \(n\) subyek terhadap \(k\) perlakuan yang diberikan secara berurutan/bergantian. Reaksi-reaksi tadi dinyatakan dengan 1 untuk “sukses” atau 0 apabila dianggap “gagal”. Hasil yang diperoleh dapat dilihat pada tabel di bawah dengan \(X_{ij}\) menyatakan 1 atau 0, sesuai reaksi subjeknya.
Format data untuk \(k\) perlakuan terhadap \(n\) subyek disajikan dalam tabel seperti berikut:
Tabel 1. Tampilan data hasil observasi atau pengamatan

di mana:
\(X_{ij}\) = jawaban (sukses atau gagal) yang diberikan subyek ke-I atas perlakuan ke-j terhadap subjek tersebut.
\(L_i\) = jumlah jawaban sukses dari subyek ke-i
\(G_k\) = jumlah jawaban sukses atas perlakuan ke-j
\(i = 1,2,…,n; \ j = 1, 2, …,k \)
Cochran mengatakan bahwa total banyaknya kejadian yang sukses (skor 1) dalam suatu kelompok dianggap tetap. Jika hipotesis nol benar, setiap perlakuan dianggap sama-sama memiliki peluang untuk menghasilkan salah satu dari skor 1 ini. Adapun statistik uji untuk Cochran adalah:
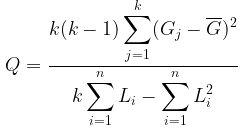
di mana:
\(G_j\) = jumlah keseluruhan ‘sukses’ dalam kolom ke-j
\( \overline{G} = \) rata-rata Gj
\(L_i\) = jumlah keselurhan ‘sukses’ dalam baris ke-i
Rumus yang ekivalen dengan rumus di atas adalah:
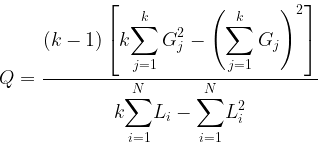
Prosedur Uji Cochran Q
- Tentukan hipotesis nol dan hipotesis alternatif. \(H_0\):Proporsi atau frekuensi jawaban sukses sama dalam masing-masing perlakuan. \(H_1\): Proporsi atau frekuensi jawaban sukses minimal ada satu yang berbeda dalam masing-masing perlakuan.
- Tentukan taraf signifikansi \((α)\)
- Hitung statistik uji. Isikan skor 1 untuk setiap “sukses” dan skor 0 untuk setiap “gagal” pada tabel \(n \times k\) seperti diberikan di atas.
- Tentukan wilayah kritis. Tingkat signifikansi harga observasi Q dapat ditentukan dengan melihat Tabel Chi-Square, karena Q mendekati distribusi chi-square dengan derajat bebas \(db= k – 1\). Tolak \(H_0\) jika \(Q ≥ χ^2 (α,k-1)\) atau jika p-value ≤ α.
- Keputusan:
- Kesimpulan.
Contoh Soal 1:
Manajer Produksi PT AMAN sedang mempertimbangkan pembelian tiga buah Mesin untuk merakit komponen tertentu. Manajer tersebut memutuskan untuk mengambil 8 orang Pekerja sebagai sampel, dan masing-masing pekerja diminta bekerja dengan masing-masing dari ketiga Mesin tersebut. Kepada setiap Mesin, tiap pekerja memberi penilaian sebagai berikut:
- Angka 0 jika kinerja mesin dirasakan tidak memuaskan.
- Angka 1 jika kinerja mesin dirasakan memuaskan.
Berikut adalah hasil penilaian kedelapan Pekerja:
| PEKERJA | MESIN A | MESIN B | MESIN C |
|---|---|---|---|
| 1 | 0 | 0 | 1 |
| 2 | 0 | 1 | 0 |
| 3 | 1 | 1 | 0 |
| 4 | 1 | 1 | 1 |
| 5 | 1 | 0 | 0 |
| 6 | 0 | 0 | 1 |
| 7 | 0 | 1 | 1 |
| 8 | 0 | 0 | 0 |
Keterangan pada baris pertama: Pekerja nomor satu menilai Mesin A adalah 0 (tidak memuaskan), Mesin B juga dengan 0, dan mesin C dengan 1 (memuaskan kinerjanya). Demikian seterusnya untuk data yang lain. Perhatikan bahwa input data hanya dua, yaitu 1 atau 0.
Tentukanlah apakah ketiga mesin memberikan kinerja yang relatif sama?
Pembahasan:
Hipotesis:
\(H_0\): Semua perlakuan mempunyai efek yang sama. Atau, dalam kasus ini ketiga mesin mempunyai kinerja yang sama.
\(H_1\): Tidak semua perlakuan mempunyai efek yang sama. Atau, dalam kasus ini ketiga mesin mempunyai kinerja yang berbeda.
Tingkat signifikansi: \(\alpha = 5\%\)
Uji statistik:
| PEKERJA | MESIN A | MESIN B | MESIN C | \(L_i\) | \(L_i^2\) |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 1 | 1 |
| 2 | 0 | 1 | 0 | 1 | 1 |
| 3 | 1 | 1 | 0 | 2 | 4 |
| 4 | 1 | 1 | 1 | 3 | 9 |
| 5 | 1 | 0 | 0 | 1 | 1 |
| 6 | 0 | 0 | 1 | 1 | 1 |
| 7 | 0 | 1 | 1 | 2 | 4 |
| 8 | 0 | 0 | 0 | 0 | 0 |
| \(G_1=3\) | \(G_1=4\) | \(G_1=4\) | \( \displaystyle \sum_{i=1}^{8} L_i = 11\) | \( \displaystyle \sum_{i=1}^{8} L_i^2 = 21\) |
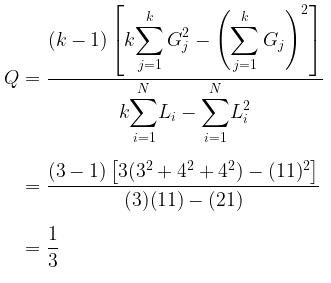
Selanjutnya, dengan melihat tabel chi-square untuk tingkat signifikansi 5% dan derajat bebas \((db) = k - 1 = 3 - 1 = 2\), diperoleh nilai chi-square tabel sebesar 5,99.
Keputusan: Karena nilai statistik hitung Q lebih kecil dari nilai chi-square tabel yakni \(\frac{1}{3} < 5,99\), maka keputusan gagal tolak \(H_0\).
Kesimpulan: Dengan tingkat signifikansi 5%, dapat disimpulkan bahwa ketiga mesin mempunyai kinerja yang relatif sama.
Sumber:
Siegel, Sidney. 1997. Statistika Nonparametrik untuk Ilmu-ilmu Sosial. Jakarta: PT Gramedia Pustaka Utama
Santoso, Singgih. 2018. Menguasai SPSS Versi 25. Jakarta: PT Elex Media Komputindo.
Artikel Terkait
I am strong because I've been weak. I am fearless because I've been afraid. I am wise because I've been foolish.
Unknown