
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
STATISTIKA MATEMATIKA II
Statistika Matematika II
Pendugaan Titik
Kriteria Pendugaan yang Ideal
Pendugaan Interval
Statistika Matematika II » Estimasi Titik › Metode Moment: Distribusi Uniform Kontinu
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552
Estimasi Titik
Metode Moment: Distribusi Uniform Kontinu
Pada artikel ini kita akan menggunakan metode momen untuk memperoleh estimator atau penduga bagi parameter suatu populasi yang berdistribusi uniform kontinu.
Sebagaimana telah kita ketahui bahwa terdapat beberapa metode estimasi parameter populasi, misalnya metode maksimum likelihood, metode bayesian, dan metode momen. Pada artikel ini kita akan menggunakan metode estimasi momen (method of moments estimation) untuk memperoleh estimator bagi parameter suatu populasi yang berdistribusi uniform kontinu.
Kasus 1: Salah satu batas interval diketahui
Suatu sampel acak dengan \(n\) pengamatan, \(X_1,X_2,…,X_n\), dipilih dari populasi di mana \(X_i\) untuk \(i=1,2,…,n\) mempunyai fungsi kepadatan peluang uniform dengan interval \((0,θ)\) di mana \(θ\) tidak diketahui. Gunakan metode momen untuk mengestimasi parameter \(θ\).
Pembahasan:
Untuk mencari estimator bagi parameter \(θ\) dari suatu distribusi uniform kontinu, pertama kita perlu tentukan momen populasi dan momen sampelnya yang bersesuaian. Momen populasinya yaitu:
\begin{align*} μ_1' = E(X) = \frac{θ}{2} \end{align*}
Adapun momen sampel yang bersesuaian, yaitu:
\begin{align*} M_1' = \frac{1}{n} \sum_{i=1}^n x_i =\overline{x} \end{align*}
Dengan menyamakan momen populasi dengan momen sampelnya yang bersesuaian, dan kemudian menyelesaikan persamaan tersebut akan diperoleh estimator bagi parameter \(θ\) yang diinginkan, yakni
\[ μ_1' = M_1' ⇒ \frac{θ}{2} = \overline{x} ⇒ \hat{θ}_{MM} = 2 \ \overline{x} \]
Jadi, berdasarkan metode momen (method of moments, MM), estimator atau penduga titik bagi parameter distribusi uniform kontinu yaitu \( \hat{θ}_{MM} = 2 \ \overline{x} \).
Kasus 2: Dua batas interval tidak diketahui
Misalkan \(X_1,X_2,…,X_n\) adalah sampel acak bebas dari distribusi uniform dengan interval \((θ_1,θ_2)\) di mana \(-∞ < θ_1 < θ_2 < ∞\). Gunakan metode momen untuk mencari estimator bagi parameter \(θ_1\) dan \(θ_2\) yang tidak diketahui.
Pembahasan:
Kita tahu bahwa fungsi kepadatan peluang (probability density function, pdf) dari distribusi uniform kontinu dengan parameter \(θ_1\) dan \(θ_2\), yaitu:
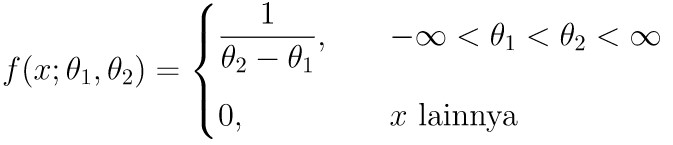
Untuk mencari estimator bagi parameter \(θ_1\) dan \(θ_2\) dari suatu distribusi uniform kontinu, pertama kita perlu tentukan momen populasi dan momen sampel. Karena di sini terdapat dua parameter populasi, yakni \(θ_1\) dan \(θ_2\) maka kita perlu mencari momen populasi dan momen sampel pertama dan kedua.
Momen populasi pertama dan keduanya, yaitu:
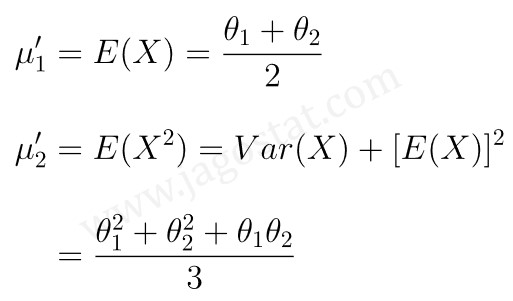
Adapun momen sampel pertama dan keduanya yang bersesuaian, yaitu:
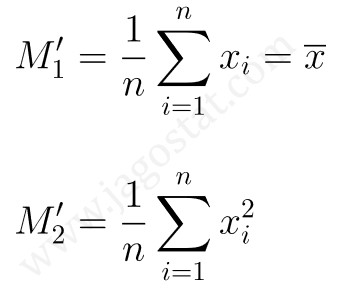
Samakan momen populasi pertama dan momen sampelnya yang bersesuaian, sehingga diperoleh:
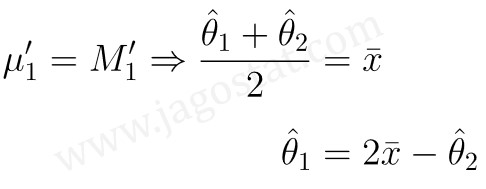
Begitu pula, dengan menyamakan momen populasi kedua dengan momen sampelnya yang bersesuaian, dan substitusi nilai \(\hat{θ}_1\) yang dihasilkan di atas sehingga diperoleh:

Untuk menyelesaikan persamaan di atas, kurangkan dengan \( 3 \bar{x}^2 \) pada kedua ruas persamaan sehingga diperoleh
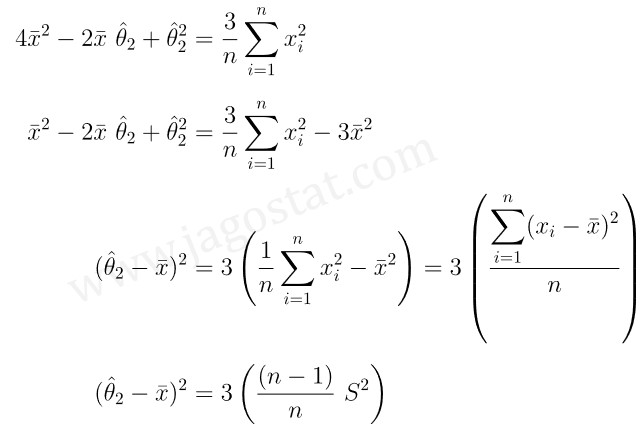
Perhatikan bahwa karena \(θ_2 > E(X)\), maka
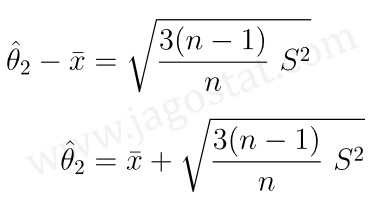
Selanjutnya, substitusi \( \hat{θ}_2 \) yang diperoleh di atas ke persamaan \( \hat{θ}_1 \) sehingga diperoleh:
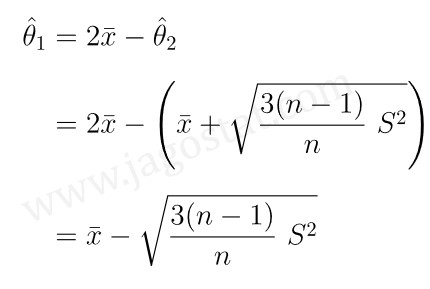
Jadi, berdasarkan metode momen (method of moments, MM), estimator titik bagi parameter \(θ_1\) dan \(θ_2\) dari suatu populasi yang berdistribusi uniform kontinu, yaitu:
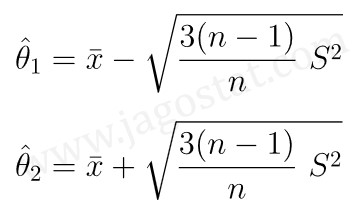
Artikel Terkait
If you born poor, it's not your mistake. But if you die poor it's your mistake.
Bill Gates
