Statistika Matematika II   »   Estimasi Titik   ›   Metode Moment: Distribusi Normal

Estimasi Titik

Metode Moment: Distribusi Normal

Pada artikel ini kita akan menggunakan metode momen untuk memperoleh estimator atau penduga bagi parameter distribusi normal yang tidak diketahui.

---

Sebagaimana telah kita ketahui bahwa terdapat beberapa metode estimasi parameter populasi, misalnya metode maksimum likelihood, metode bayesian, dan metode momen. Pada artikel ini kita akan menggunakan metode momen (method of moments estimation) untuk memperoleh estimator atau penduga bagi parameter suatu populasi yang berdistribusi normal.

Misalkan \(X_1,…,X_n\) adalah sampel acak (random samples) dari populasi yang berdistribusi normal dengan parameter rata-rata \(μ\) dan varians \(σ^2\), yakni \(X_i \sim N(μ, σ^2)\). Dengan menggunakan metode momen, tentukan estimator titik bagi parameter \(μ\) dan \(σ^2\) yang tak diketahui.

Pembahasan:

Kita tahu bahwa fungsi kepadatan peluang (probability density function, pdf) dari distribusi normal dengan parameter \(μ\) dan \(σ^2\), yaitu:

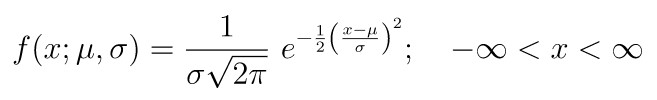
Untuk mencari estimator bagi parameter \(μ\) dan \(σ^2\) dari suatu distribusi normal, pertama kita perlu tentukan momen populasi dan momen sampel. Karena di sini terdapat dua parameter populasi, yakni \(μ\) dan \(σ^2\) maka kita perlu mencari momen populasi dan momen sampel pertama dan kedua.

Momen populasi pertama dan keduanya, yaitu:

Adapun momen sampel pertama dan keduanya, yaitu:

Dengan menyamakan momen populasi pertama dengan momen sampelnya yang bersesuaian, dan kemudian menyelesaikan persamaan tersebut akan diperoleh estimator bagi parameter \(μ\) yang diinginkan, yakni

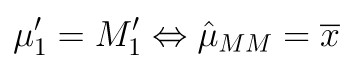
Begitu pula, dengan menyamakan momen populasi kedua dengan momen sampelnya yang bersesuaian akan diperoleh estimator bagi parameter \(σ^2\), yakni:

Catatan:

Jadi, berdasarkan metode momen (method of moments, MM), estimator titik bagi parameter \(μ\) dan \(σ^2\) dari suatu populasi yang berdistribusi normal yaitu