
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
STATISTIKA MATEMATIKA II
Statistika Matematika II
Pendugaan Titik
Kriteria Pendugaan yang Ideal
Pendugaan Interval
Statistika Matematika II » Estimasi Titik › Metode Maksimum Likelihood (MLE): Distribusi Uniform Kontinu
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552
Estimasi Titik
Metode Maksimum Likelihood (MLE): Distribusi Uniform Kontinu
Pada artikel ini kita akan gunakan metode maksimum likelihood untuk memperoleh estimator atau penduga bagi parameter distribusi uniform kontinu.
Salah satu metode estimasi yang cukup populer dan sering diaplikasikan dalam berbagai penelitian yaitu metode maksimum likelihood. Gagasan dari metode ini yaitu mencari estimator atau penduga bagi parameter populasi yang dapat memaksimalkan fungsi likelihood.
Pada artikel ini kita akan menggunakan metode estimasi maksimum likelihood atau biasa disingkat metode mle (maximum likelihood estimation) untuk memperoleh estimator atau penduga bagi parameter suatu populasi yang berdistribusi uniform kontinu.
Baca juga:
Misalkan \(X_1,X_2,…,X_n\) adalah sampel acak dari suatu populasi yang berdistribusi uniform dengan fungsi kepadatan peluangnya yaitu \(f(y_i;θ)=1/θ\), untuk \(0≤y_i≤θ\) dan \(i=1,2,…,n\). Gunakan metode mle untuk mencari estimator bagi parameter \(θ\).
Pembahasan:
Dalam kasus ini, fungsi likelihoodnya yaitu:
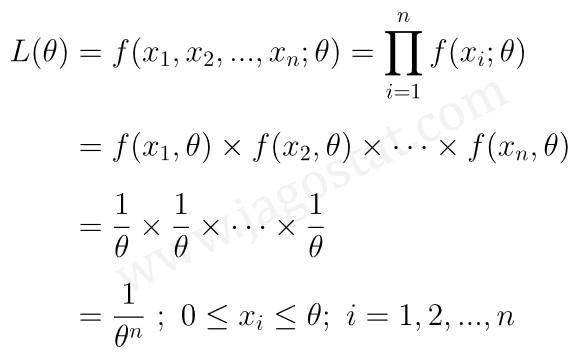
Ingat bahwa inti dari metode mle yaitu mencari estimator bagi parameter yang dapat memaksimumkan fungsi likelihood. Lantas, bagaimana caranya memaksimumkan fungsi likelihood yang kita peroleh di atas?
Perhatikan bahwa \(1/θ^n\) adalah fungsi dari \(θ\) yang menurun secara monoton sebagaimana tampak pada Gambar 1. Oleh karena itu, tidak ada nilai dalam interval \(0 < θ < ∞\) di mana \(\frac{d[1/θ^n]}{dθ}\) akan bernilai sama dengan nol. Namun, \(1/θ^n\) meningkat ketika \(θ\) menurun, dan \(1/θ^n\) akan maksimum dengan memilih nilai \(θ\) yang sekecil mungkin, dengan syarat bahwa semua nilai \(x_i\) berada di antara nol dan \(θ\).
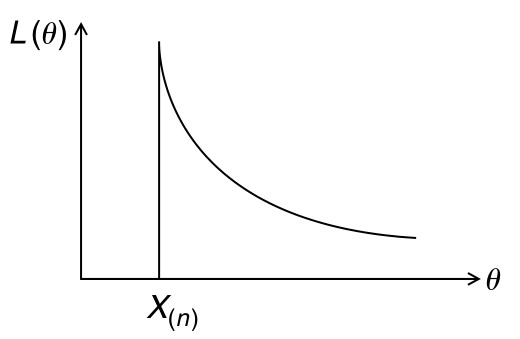
Gambar 1. Grafik fungsi likelihood dari distribusi uniform kontinu
Nilai \(θ\) terkecil yang memenuhi kondisi tersebut yaitu nilai pengamatan paling besar dari sekumpulan pengamatan \(x_1,x_2,…,x_n\). Dengan kata lain, \(\hat{θ}=X_{(n)}=\max(X_1,X_2,…,X_n)\) adalah estimator maksimum likelihood (MLE) bagi parameter \(θ\). Estimator \(\hat{θ}=Y_{(n)}\) merupakan estimator yang bias bagi parameter \(θ\), tetapi ia bisa dibuat atau disesuaikan sedemikian rupa sehingga menjadi estimator yang tidak bias.
Dua contoh estimator \(\hat{θ}=X_{(n)}=\max(X_1,X_2,…,X_n)\) yang telah disesuaikan sehingga menjadi estimator tak bias bagi parameter \(θ\), yaitu:
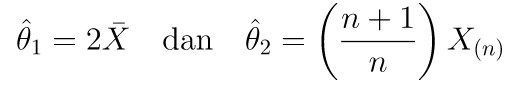
Artikel Terkait
Be not afraid of growing slowly, be afraid only of standing still.
Chinese Proverb
