Statistika Matematika II   »   Estimasi Titik   ›   Metode Maksimum Likelihood (MLE): Distribusi Gamma

Estimasi Titik

Metode Maksimum Likelihood (MLE): Distribusi Gamma

Pada artikel ini kita akan menggunakan metode estimasi maksimum likelihood untuk memperoleh estimator atau penduga bagi parameter distribusi gamma.

---

Salah satu metode estimasi yang cukup populer dan sering diaplikasikan dalam berbagai penelitian yaitu metode maksimum likelihood. Gagasan dari metode ini yaitu mencari estimator atau penduga bagi parameter populasi yang dapat memaksimalkan fungsi likelihood.

Pada artikel ini kita akan menggunakan metode estimasi maksimum likelihood atau biasa disingkat metode mle (maximum likelihood estimation) untuk memperoleh estimator atau penduga bagi parameter suatu populasi yang berdistribusi gamma.

Misalkan \(X_1,…,X_n\) adalah sampel acak (random samples) dari suatu populasi yang berdistribusi gamma dengan parameter \(α\) dan \(β\). Carilah MLE atau estimator maksimum likelihood (maximum likelihood estimators) bagi parameter \(α\) dan \(β\) yang tidak diketahui.

Pembahasan:

Kita tahu bahwa fungsi kepadatan peluang (probability density function, pdf) dari distribusi gamma dengan parameter \(α\) dan \(β\), yaitu:

Untuk mencari MLE bagi parameter distribusi gamma, kita perlu tentukan dulu fungsi likelihoodnya, yakni:

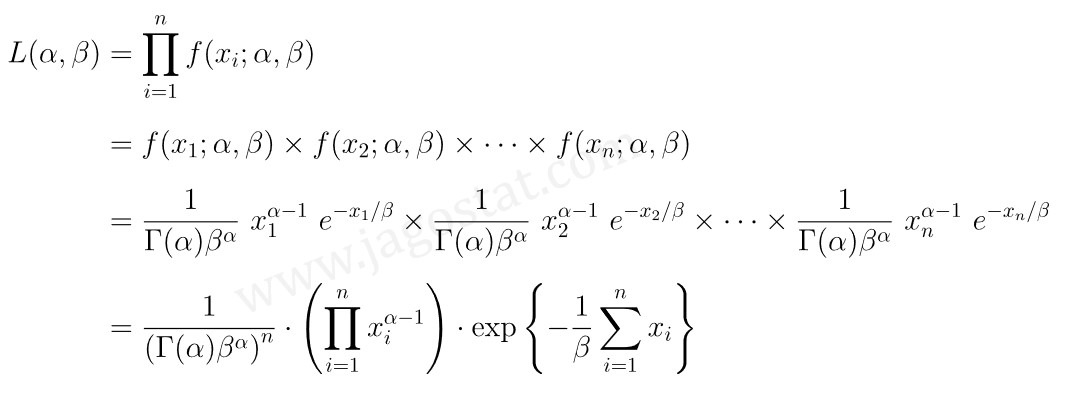
Setelah itu, kita cari \(\ln \ L(\alpha, \beta)\) yakni:

Selanjutnya yaitu memaksimumkan fungsi \(\ln \ L(\alpha, \beta)\) yang diperoleh di atas dengan cara mencari turunan pertama masing-masing terhadap \(\alpha\) dan \(\beta\) dan menyamakan hasil turunan tersebut dengan nol. Kemudian selesaikan persamaan untuk mendapatkan estimator yang diinginkan.

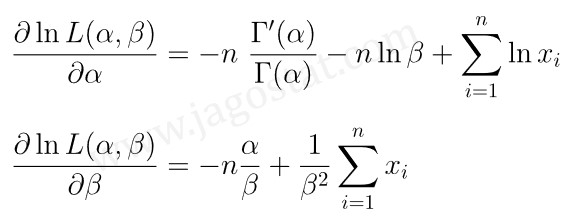
Dengan menyamakan turunan fungsi \(\ln \ L(\alpha, \beta)\) terhadap \(\beta\) sama dengan nol, kita peroleh:

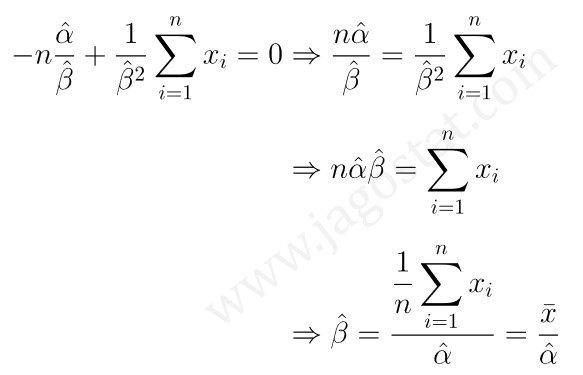
Kemudian dengan substitusi nilai \(\hat{β}=\bar{x}/\hat{\alpha}\) ke persamaan turunan \(\ln \ L(\alpha, \beta)\) terhadap \(α\) dan menyamakan hasilnya dengan nol, maka kita peroleh:

Perhatikan bahwa tidak ada solusi bentuk tertutup (no closed-form solution) bagi \(\hat{α}\) dan \(\hat{β}\). Oleh karena itu, kita tidak dapat selesaikan persamaan tersebut secara langsung. Dalam kasus ini, kita bisa gunakan pendekatan numerik seperti metode Newton-Raphson untuk mencari nilai \(\hat{α}\) dan kemudian menggunakan nilai tersebut untuk mencari \(\hat{β}\).

Metode estimasi parameter populasi lainnya dikenal dengan metode momen (method of moments estimation). Dengan menggunakan metode momen, kita peroleh estimator bagi parameter distribusi gamma, yakni:

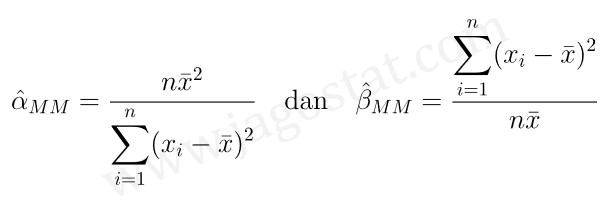
Cukup sekian penjelasan mengenai penggunaan metode MLE untuk mengestimasi parameter distribusi gamma yang tidak diketahui dalam artikel ini. Semoga bermanfaat.