Analisis Time Series   »   Model Time Series Musiman   ›  Identifikasi Model SARIMA

Model Time Series

Identifikasi Model SARIMA

Dalam identifikasi model SARIMA, kita perlu menentukan orde dari nonmusiman (p, d, dan q) dan orde dari model musimannya (P, D, dan Q).

---

Jika Anda telah membaca artikel terkait identifikasi model AR, MA, ARMA atau model ARIMA, maka Anda harusnya tidak kesulitan memahami penjelasan dalam artikel ini. Karena pada dasarnya, prosedur yang diterapkan hampir sama yakni menggunakan plot ACF dan PACF sampel untuk mengidentifikasi model.

Hanya saja dalam identifikasi model musiman (dalam hal ini model SARIMA), selain mengidentifikasi atau menentukan orde dari model nonmusiman (p, d, dan q), kita juga perlu mengidentifikasi orde musimanannya yakni P, D, dan Q.

Agar lebih jelas, mari kita simak contoh berikut ini.

Contoh 1:

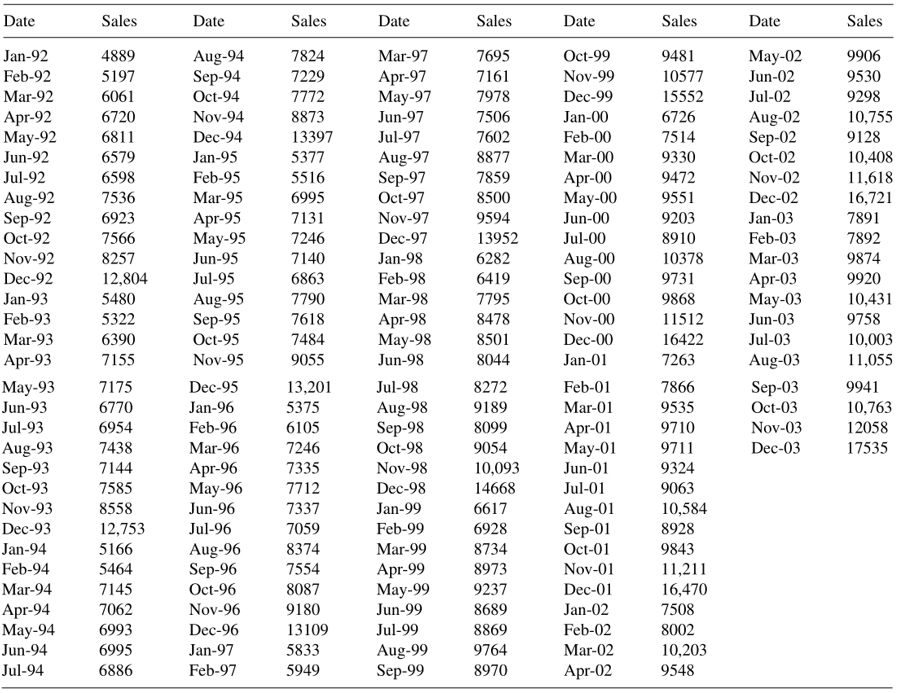
Tabel 1 berikut menunjukkan data penjualan produk pakaian AS (US clothing sales data). Plot dari data ini diberikan pada Gambar 1 di bawah. Data ini dengan jelas menunjukkan adanya pola musiman dan tren linier ke atas.

Tabel 1. Data penjualan produk pakaian AS

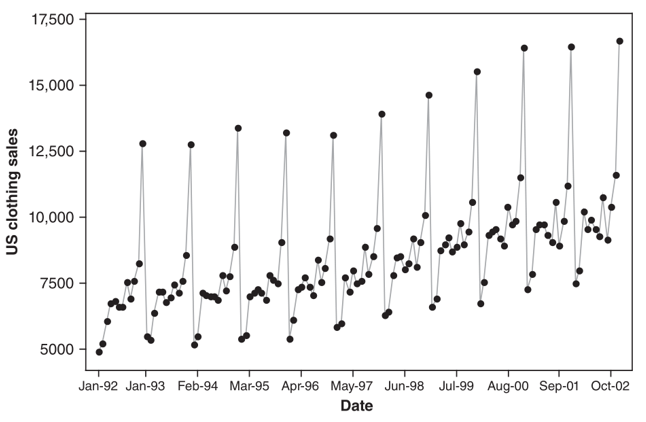
Gambar 1. Plot data penjualan produk pakaian AS

Plot ACF dan PACF sampel dari data ini diberikan pada Gambar 2 berikut.

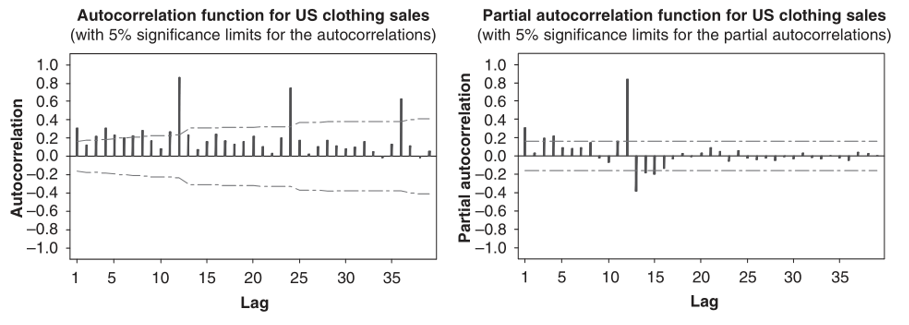
Gambar 2. Plot ACF dan PACF sampel dari data penjualan produk pakaian AS

Gambar 2 menunjukkan adanya periodisasi musiman secara bulanan (s = 12), karena nilai ACF pada lag 12, 24, 36 adalah signifikan (nilainya berada di luar interval/garis mendatar) dan menurun secara perlahan, dan ada nilai PACF yang signifikan pada lag 12 yang mendekati nilai 1.

Selain itu, umumnya ACF yang menurun perlahan juga menunjukkan nonstasioneritas yang mana dapat diatasi dengan melakukan pembedaan pertama (first difference). Oleh karena itu, kita lakukan pembedaan pertama dan juga pembedaan musiman (seasonal differencing), yakni

\[ w_t=(1-B)(1-B^{12}) y_t \]

Gambar 3 di bawah menunjukkan bahwa pembedaan pertama bersamaan dengan pembedaan musiman telah berhasil membuat data menjadi stasioner dan menghilangkan pengaruh musiman yang mana terlihat pada plot ACF dan PACF dalam Gambar 4.

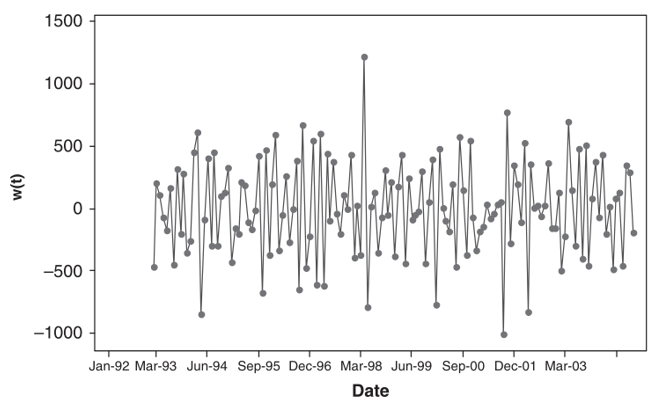
Gambar 3. Data setelah dilakukan pembedaan pertama dan pembedaan musiman

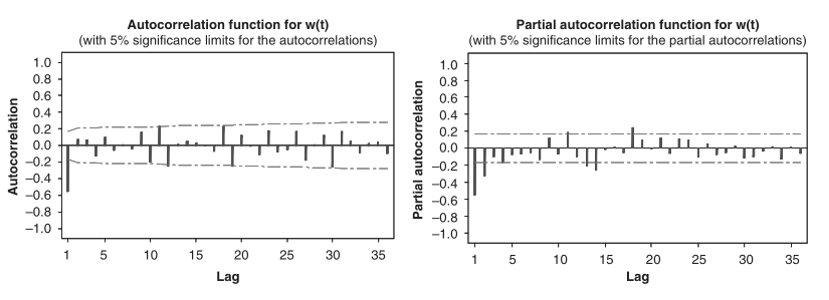
Gambar 4. Plot ACF dan PACF setelah dilakukan pembedaan pertama dan pembedaan musiman

Perhatikan Gambar 4. Nilai ACF sampel signifikan pada lag 1 dan pola PACF tampak turun secara eksponensial pada 8 lag pertama yang mana menyarankan bahwa model MA(1) nonmusiman seharusnya diterapkan.

Untuk interpretasi musiman akan sedikit lebih sulit. Untuk itu, kita harus fokus pada nilai ACF dan PACF sampel pada lag 12, 24, 36, dan seterusnya. ACF sampel pada lag 12 tampak signifikan dan PACF sampel pada lag 12, 24, 36 (meskipun tidak signifikan) tampak bergantian tanda (dari positif ke negatif, dan sebaliknya).

Hal ini menandakan bahwa model MA(1) musiman juga dapat digunakan. Dengan demikian model ARIMA\((0, 1, 1) × (0, 1, 1)^{12}\) digunakan untuk memodelkan data \(y_t\).

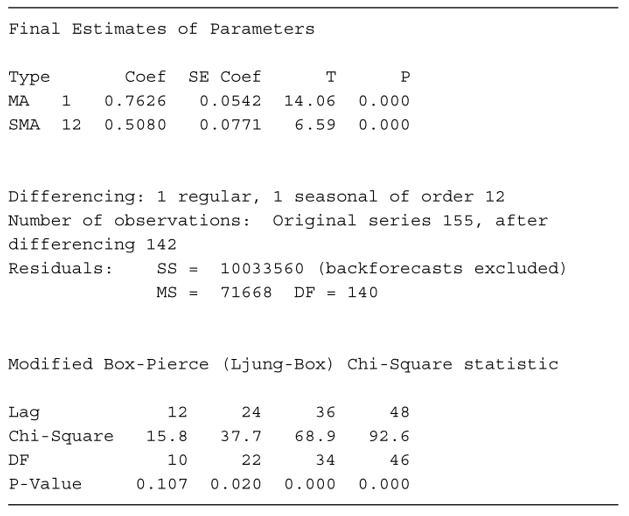
Output Minitab disajikan pada Tabel 2. Baik itu estimasi koefisien MA (1) nonmusiman maupun MA(1) musiman adalah signifikan. Adapun plot ACF dan PACF residualnya ditunjukkan pada Gambar 5.

Tabel 2. Output Minitab untuk model ARIMA\((0, 1, 1) × (0, 1, 1)^{12}\)

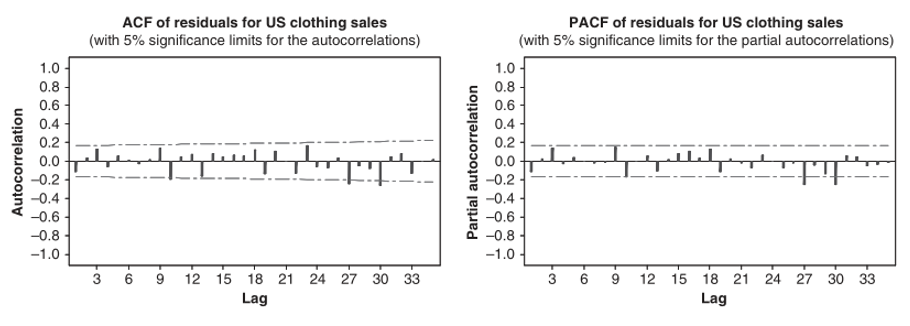
Gambar 5. Plot ACF dan PACF residual dari model ARIMA\((0, 1, 1) × (0, 1, 1)^{12}\)

Plot residual pada Gambar 6, juga tampak dapat diterima.

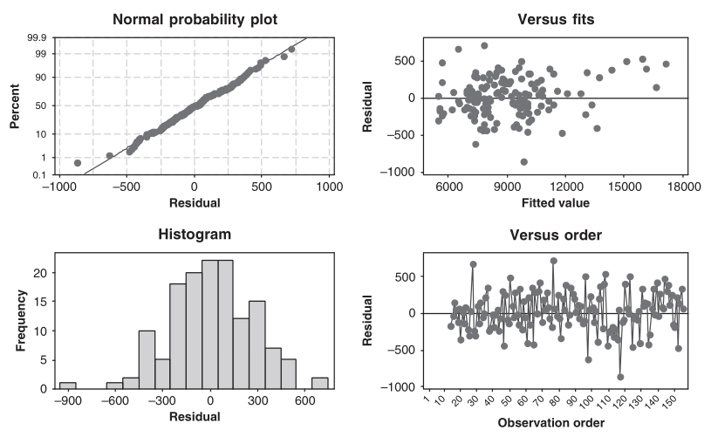
Gambar 6. Plot residual dari model ARIMA \((0, 1, 1) × (0, 1, 1)^{12}\)

Terakhir, plot time series untuk nilai aktual dan nilai fit pada Gambar 7 berikut menunjukkan bahwa model ARIMA \((0, 1, 1) × (0, 1, 1)^{12}\) memberikan nilai fit yang beralasan (reasonable fit) untuk data time series dengan pola musiman yang kuat dan nonstasioner.

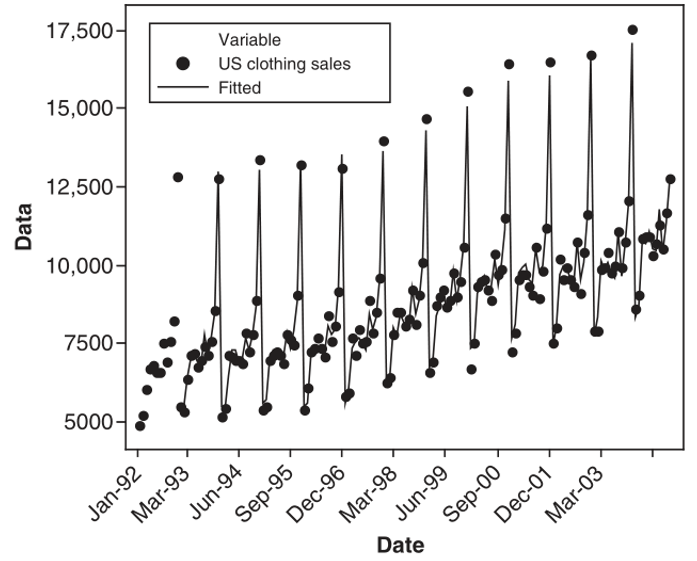
Gambar 7. Plot time series untuk nilai aktual dan fit berdasarkan model ARIMA\((0, 1, 1) × (0, 1, 1)^{12}\)