Analisis Time Series   »   Konsep Dasar Time Series   ›  Fungsi Autokorelasi Parsial (Partial Autocorrelation Function)

Autokorelasi Parsial

Fungsi Autokorelasi Parsial (Partial Autocorrelation Function)

Dalam analisis time series, terdapat dua konsep penting yang dikenal dengan fungsi autokorelasi (autocorrelation function, ACF) dan fungsi autokorelasi parsial (partial autocorrelation function, PACF). Kedua jenis korelasi tersebut biasanya digunakan dalam spesifikasi model.

Untuk memahami PACF dengan lebih mudah, ada baiknya kita mengingat kembali konsep korelasi parsial (partial correlation) terlebih dulu.

Partial Correlation

Umumnya, korelasi parsial adalah korelasi bersyarat (conditional correlation) yakni korelasi antara dua variabel di bawah asumsi bahwa kita mengetahui dan memperhitungkan nilai dari beberapa set variabel lainnya.

Sebagai contoh, dalam konteks regresi di mana \(y\) adalah variabel dependen dan \(x_1,x_2\), dan \(x_3\) adalah variabel independen, maka korelasi parsial antara \(y\) dan \(x_3\) adalah korelasi yang telah memperhitungkan bagaimana y dan \(x_3\) berkaitan dengan \(x_1\) dan \(x_2\).

Partial Autocorrelation Function (PACF)

Dengan mengikuti definisi korelasi parsial di atas, maka untuk data time series, autokorelasi parsial antara \(y_t\) dan \(y_{t-k}\) adalah korelasi antara \(y_t\) dan \(y_{t-k}\) setelah menyesuaikan (adjusting for) atau memperhitungkan (taking into account) nilai dari \(y_{t-1},y_{t-2},…,y_{t-k+1}\).

Oleh karena itu, untuk model AR(p), PACF antara \(y_t\) dan \(y_{t-k}\) di mana \(k > p\), seharusnya sama dengan nol. Adapun definisi formalnya diberikan berikut ini.

• Autokorelasi parsial orde (lag) pertama sama dengan autokorelasi lag pertama. Untuk autokorelasi parsial lag kedua, dapat diperoleh sebagai berikut:

• Sedangkan, autokorelasi parsial lag ketiga dapat diperoleh dari:

• Demikian seterusnya untuk autokorelasi parsial lag selanjutnya.

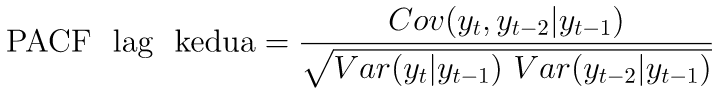
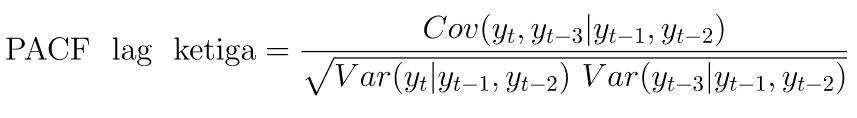
Biasanya, manipulasi matriks yang berkaitan dengan matriks kovarians dari distribusi multivariat digunakan untuk menentukan estimasi autokorelasi parsial.

Sama seperti ACF, nilai PACF berkisar antara +1 dan -1.