Analisis Time Series   »   Model Time Series Musiman   ›  Model SARIMA (Seasonal ARIMA)

Model Time Series

Model SARIMA (Seasonal ARIMA)

Salah model untuk merepresentasikan data time series yang memiliki perilaku musiman (seasonal) dikenal dengan Model SARIMA (Seasonal ARIMA).

---

Data time series terkadang menunjukkan adanya pola periodisasi yang kuat. Data seperti ini sering disebut sebagai data time series yang memiliki perilaku musiman. Perilaku musiman ini dapat diartikan sebagai sebuah pola perubahan yang tetap dan berulang selama periode waktu S, di mana S didefinisikan sebagai periode waktu sampai pola berulang kembali.

Perilaku musiman sebagian besar terjadi ketika data diambil dalam interval tertentu — bulanan, mingguan, dan seterusnya. Sebagai contoh, pola musiman untuk data bulanan terjadi ketika nilai tinggi cenderung muncul pada beberapa bulan tertentu dan nilai rendah cenderung muncul pada beberapa bulan tertentu lainnya. Dalam kasus ini, S = 12 merupakan rentang dari periode musiman. Untuk data triwulanan, S = 4.

Terdapat beberapa model untuk peramalan data time series musiman. Salah satu model yang kita bahas yaitu model SARIMA (seasonal ARIMA) yang merupakan perluasan dari model ARIMA.

Dalam model ARIMA musiman (seasonal ARIMA), model AR musiman memprediksi \(y_t\) menggunakan nilai data pada lag dengan kelipatan S (rentang musiman), sedangkan model MA musiman memprediksi \(y_t\) menggunakan error dengan lag yang merupakan kelipatan S.

Sebagai contoh, untuk data bulanan (S = 12), model AR orde pertama menggunakan \(y_{t-12}\) untuk memprediksi \(y_t\). Misalnya, kita memprediksi penjualan pakaian pada Juli ini menggunakan penjualan pada Juli tahun lalu. Sementara itu, untuk model AR orde kedua kita menggunakan \(y_{t-12}\) dan \(y_{t-24}\) untuk memprediksi \(y_t\). Dengan kata lain, kita gunakan data penjualan pada Juli dua tahun sebelumnya untuk memprediksi penjualan pada Juli saat ini.

Pada model MA musiman dengan orde 1 (S = 12), kita gunakan \(w_{t-12}\) sebagai prediktor (w = error). Sedangkan, untuk model MA musiman orde 2, kita gunakan \(w_{t-12}\) dan \(w_{t-24}\).

Pembedaan Musiman

Perilaku musiman biasanya menyebabkan data menjadi tidak stasioner. Ini dapat diatasi dengan melakukan pembedaan musiman (seasonal differencing) yang didefinisikan sebagai selisih antara nilai variable dengan nilai variabel pada lag yang merupakan kelipatan S.

Misalnya, untuk S = 12 (data bulanan), maka pembedaan musiman dapat didefinisikan sebagai

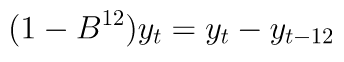
Hasil dari pembedaan musiman ini akan mendekati sama untuk tiap bulan pada tahun tersebut sehingga memberikan series yang stasioner. Sedangkan untuk S = 4, maka pembedaan musimannya yaitu:

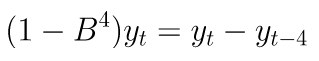
Kadang kala, data time series menunjukkan perilaku musiman dengan tren yang meningkat seperti terlihat pada plot berikut.

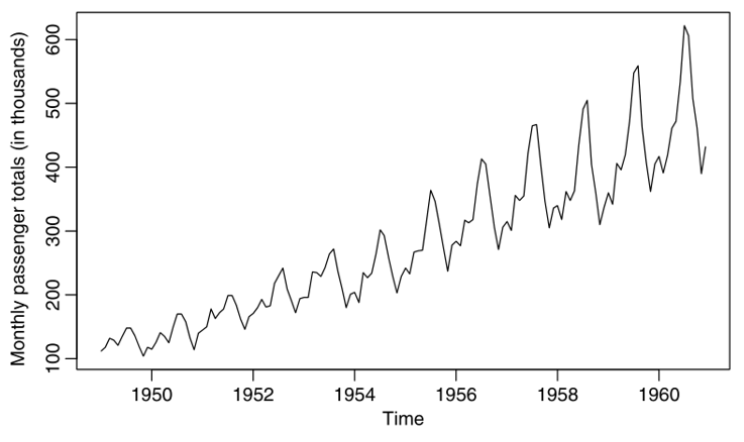
Gambar 1. Plot data musiman dengan tren meningkat

Untuk data demikian, selain pembedaan musiman, kita mungkin juga perlu melakukan pembedaan nonmusiman (nonseasonal differencing). Biasanya (tidak selalu) pembedaan pertama (first difference) akan menghilangkan tren pada data dan karena itu menjadi stasioner.

Sebagaimana telah kita pelajari bahwa pembedaan nonmusiman pertama didefinisikan sebagai:

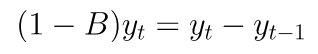
Dengan demikian, jika kita menerapkan pembedaan nonmusiman dan pembedaan musiman pertama (untuk S = 12), maka kita peroleh

Notasi Model SARIMA

Model ARIMA musiman menggabungkan faktor nonmusiman dan musiman dalam model multiplikatif. Salah satu notasi singkat untuk model ini yaitu:

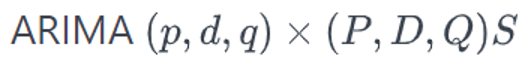
di mana: p = orde dari model AR, d = pembedaan nonmusiman, q = orde dari model MA, P = model dari model AR musiman, D = pembedaan musiman, dan Q = orde dari model MA musiman, dan S = rentang waktu di mana musiman berulang.

Tanpa adanya pembedaan musiman dan nonmusiman, model umum dari SARIMA dapat dituliskan sebagai:

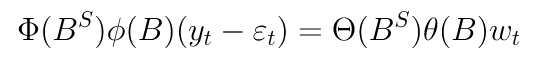
Model umum ini dapat kita uraikan menjadi komponen nonmusiman dan musiman, yakni:

1. Komponen Nonmusiman:

2. Komponen Musiman:

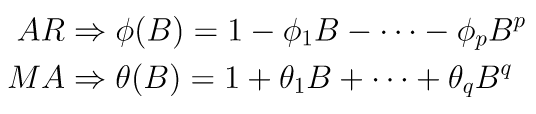
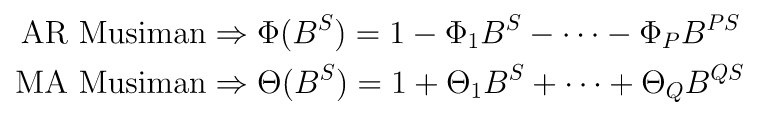
Perhatikan bahwa pada sisi kiri persamaan model umum SARIMA di atas, komponen AR musiman dan nonmusiman saling mengalikan (multiply each other), sedangkan pada sisi kanan persamaan, komponen MA musiman dan nonmusimannya juga saling mengalikan.

Beberapa Contoh Model SARIMA

Perhatikan beberapa contoh penulisan model SARIMA berikut:

Model ARIMA(0,0,1)(0,0,1)12

Model ini mencakup MA(1) nonmusiman, MA(1) musiman, tanpa pembedaan (differencing), dan tidak ada suku AR serta periode musiman adalah S = 12. Komponen untuk MA(1) nonmusiman dapat dituliskan:

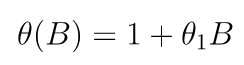
dan untuk MA(1) musimannya yaitu:

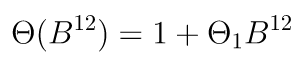
Sehingga, dengan mengacu pada model umum SARIMA, kita peroleh

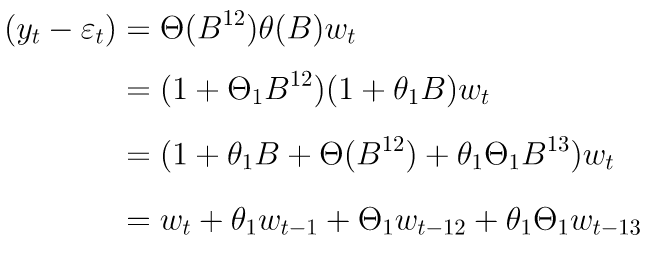
ARIMA(1,1,1)(1,1,1)4

Model SARIMA dengan pembedaan musiman dan nonmusiman ini dapat kita tuliskan sebagai berikut:

Bagaimana Menentukan Orde dari Model SARIMA?

Setelah membahas panjang lebar di atas, muncul pertanyaan bagaimana kita menentukan orde dari model SARIMA. Misalnya, bagaimana kita bisa mendapatkan model ARIMA(0,0,1)(0,0,1)12 atau ARIMA(1,1,1)(1,1,1)4?

Karena pembahasannya cukup panjang, jawaban mengenai pertanyaan ini kita bahas pada artikel selanjutnya tentang identifikasi model SARIMA. Klik link untuk melanjutkan.