Analisis Time Series   »   Model Time Series Stasioner   ›  Autoregressive Model (AR)

Model Time Series

Autoregressive Model (AR)

Model Autoregressive (AR) menghubungkan nilai pengamatan aktual dengan nilai pengamatan masa lalunya. Ini dapat dilakukan ketika sebuah pengamatan tidak lepas dari pengamatan masa lalunya.

---

Dalam analisis regresi yang melibatkan data time series, jika model regresinya mencakup tidak hanya variabel bebas (X) tetapi juga nilai lag-nya (nilai lampaunya), maka disebut distributed-lag model.

Sedangkan, jika model regresi hanya mencakup satu atau lebih nilai lag dari variabel tak bebas (dependent variable) sebagai variabel bebas (explanatory variables) pada model tersebut, maka disebut autoregressive model.

Dengan kata lain, model autoregressive (AR) adalah model regresi time series yang menghubungkan nilai pengamatan aktual dengan nilai pengamatan sebelumnya. Ini dapat dilakukan ketika sebuah pengamatan tidak lepas dari pengamatan yang terjadi sebelumnya. Konsep dasar model ini yaitu meregresikan pengamatan aktual dengan nilai pengamatan sebelumnya untuk melakukan peramalan nilai ke depan.

Adapun persamaan model autoregressive dengan order p atau AR(p) dapat dituliskan sebagai berikut:

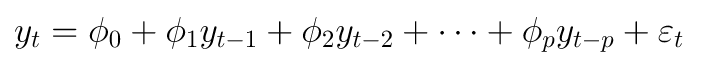
di mana: \( \varepsilon_t \sim WN(0,\sigma^2) \).

Adapun persamaan untuk distributed-lag model dapat dituliskan sebagai berikut:

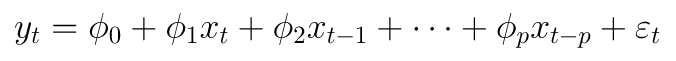
Alasan Penggunaan Lag

Dalam ilmu ekonomi, ketergantungan variabel dependen terhadap variabel penjelas jarang terjadi secara instan. Sangat sering, variabel dependen merespons variabel penjelas dengan suatu selang waktu tertentu. Selang waktu seperti itu disebut lag.

Berikut adalah alasan penggunaan lag dalam model regresi:

#1. Alasan Psikologi (Psychological reasons)

Sebagai akibat dari kekuatan kebiasaan (inersia), orang tidak mengubah kebiasaan konsumsinya segera setelah terjadi penurunan harga atau sesudah adanya peningkatan pendapatan. Dengan kata lain, kebiasaan konsumsi kita juga dipengaruhi oleh harga sebelum terjadi penurunan atau sebelum adanya peningkatan pendapatan (lag).

#2. Alasan Teknologi (Technological reasons)

Misalkan biaya penggunaan modal dalam produksi relatif terhadap tenaga kerja mengalami penurunan, maka substitusi modal untuk tenaga kerja adalah layak secara ekonomi. Akan tetapi, penambahan modal membutuhkan waktu (masa gestasi). Selain itu, jika penurunan biaya diperkirakan bersifat sementara, perusahaan mungkin tidak mau terburu-buru untuk mengganti modal dengan tenaga kerja, terutama jika mereka memperkirakan bahwa setelah terjadi penurunan yang bersifat sementara, biaya modal akan meningkat lagi melebihi tingkat sebelumnya.

Oleh karena itu, penggunaan modal tidak hanya dipengaruhi oleh biaya modal sekarang tetapi juga biaya modal periode sebelumnya (lag).

#3. Alasan institusional (Institutional reasons)

Sebagai contoh, kewajiban kontrak mungkin mencegah perusahaan beralih dari satu sumber tenaga kerja atau bahan mentah dengan sumber tenaga kerja atau bahan mentah lainnya. Contoh lain misalnya, pemberi kerja sering kali memberi karyawan mereka pilihan di antara beberapa paket asuransi kesehatan, tetapi begitu pilihan dibuat, seorang karyawan tidak boleh beralih ke paket lain selama setidaknya satu tahun.

PACF dan Orde dari Model AR(p)

Pada artikel yang lain, kita telah membahas tentang fungsi autokorelasi (autocorrelation function, ACF). Kita juga telah menjelaskan bagaimana plot ACF dapat digunakan untuk mengidentifikasi orde dari model MA(q), karena plot ACF ini diharapkan akan berhenti terpotong setelah lag q (cut off after lag q).

Untuk menentukan atau mengindentifikasi orde dari model AR(p), kita gunakan fungsi autokorelasi parsial (partial autocorrelation function, PACF). Sekarang coba amati plot PACF yang diberikan pada Gambar 1 berikut:

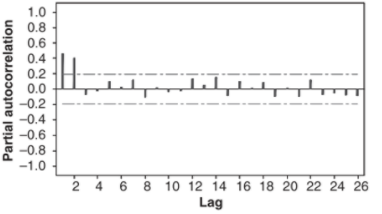
Gambar 1. Plot PACF sampel

Dari Gambar 1 di atas, terlihat bahwa plot PACF signifikan atau terpotong pada lag 1 dan 2 dan setelah itu tidak ada lagi lag yang terpotong (it cuts off after lag 2). Jadi, jika berdasarkan plot PACF sampel ini, kemungkinan model yang kita peroleh adalah model AR(2).

Sumber:

Gurajarati, Damodar N & Dawn C Porter. Basic Econometrics, 5th ed. New York: McGraw-Hill Companies, Inc.