Analisis Time Series   »   Model Time Series Stasioner   ›  Identifikasi Model AR, MA, dan ARMA

Model Time Series

Identifikasi Model AR, MA, dan ARMA

Model ARMA merupakan campuran antara model autoregressive (AR) dan moving average (MA). Model AR mengasumsikan bahwa data sekarang dipengaruhi oleh data sebelumnya, sedangkan model MA mengasumsikan bahwa data sekarang dipengaruhi oleh nilai residual data sebelumnya.

---

Konsep mengenai model autoregressive (AR), moving average (MA) dan autoregressive moving average (ARMA) dan beberapa contoh sederhana dari ketiga model tersebut untuk orde p dan q tertentu telah kita bahas pada artikel sebelumnya.

Namun, pada artikel tersebut kita belum menjelaskan bagaimana orde p dan q itu diperoleh. Oleh karena itu, dalam artikel ini kita akan membahas identifikasi model AR, MA dan ARMA dan menentukan orde dari model tersebut.

Sebagaimana telah saya bahas sebelumnya bahwa dalam analisis time series, terdapat dua konsep penting yang dikenal dengan fungsi autokorelasi (autocorrelation function, ACF) dan fungsi autokorelasi parsial (partial autocorrelation function, PACF).

Kita dapat gunakan keduanya untuk melakukan spesifikasi model time series stasioner antara AR, MA atau ARMA. Selain itu, kita juga bisa mengidentifikasi orde dari ketiga model berdasarkan plot ACF dan PACF sampel.

Untuk lebih jelasnya, kita langsung saja ke contoh berikut.

Contoh 1:

Tabel 1 di bawah menunjukkan total pengajuan pinjaman mingguan (weekly total number of loan applications) di sebuah cabang lokal dari suatu bank nasional selama 2 tahun terakhir. Diduga ada hubungan (yaitu autokorelasi) antara jumlah pengajuan pinjaman minggu sekarang dan jumlah pengajuan pinjaman pada minggu-minggu sebelumnya.

Memodelkan hubungan itu akan membantu manajemen untuk secara proaktif membuat perencanaan pada beberapa minggu mendatang melalui peramalan (forecasting) yang dapat diandalkan.

Tabel 1. Total pengajuan pinjaman mingguan selama 2 tahun terakhir

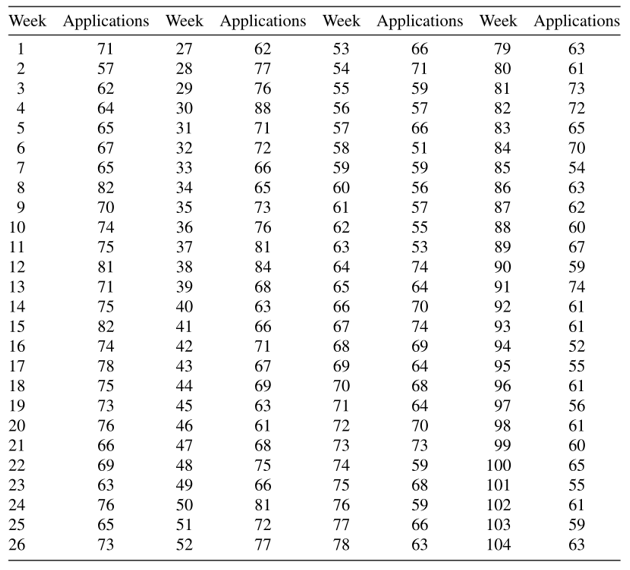
Seperti biasa, kita memulai analisis dengan plot time series yang ditunjukkan pada Gambar 1 berikut.

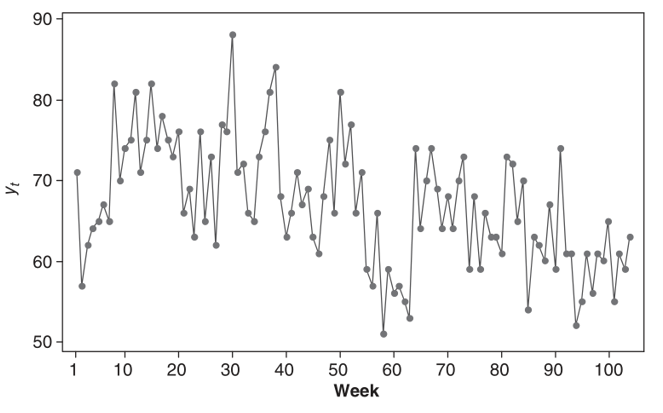
Gambar 1. Plot time series untuk total pengajuan pinjaman mingguan

Gambar 1 di atas menunjukkan bahwa data pengajuan pinjaman mingguan cenderung memiliki short runs dan karena itu data tersebut tampaknya memang berautokorelasi. Selanjutnya, kita memeriksa stasioneritas secara visual. Meskipun mungkin ada sedikit penurunan rata-rata untuk tahun kedua (minggu 53-104), secara umum, tampaknya aman untuk mengasumsikan stasioneritas.

Sekarang amati plot ACF dan PACF sampel pada Gambar 2 di bawah. Berikut adalah interpretasi yang mungkin dari plot ACF:

1. Plot ACF tidak lagi terpotong setelah lag 2 (it cuts off after lag 2) atau bahkan mungkin pada lag 3, yang mana menyarankan model MA(2) atau bahkan bisa jadi model MA(3).
2. Plot ACF mempunyai pola yang turun secara eksponensial yang mana menyarankan model AR(p).

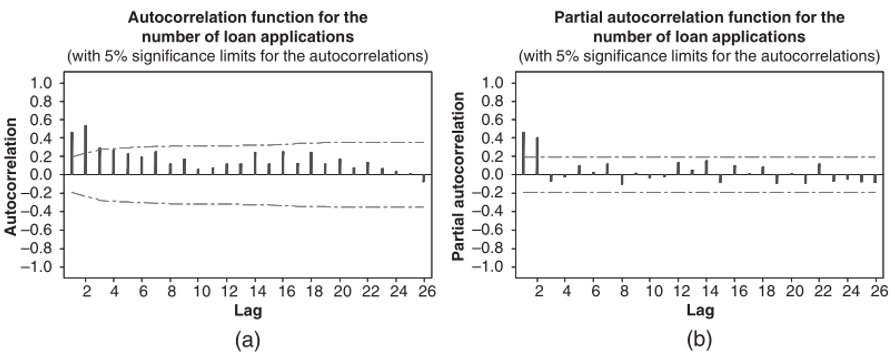
Gambar 2. Plot ACF dan PACF untuk data total pengajuan pinjaman mingguan

Jika hanya berdasarkan plot ACF sampel akan muncul pertanyaan model manakah yang seharusnya dipilih? Apakah model MA(2)/MA(3) atau model AR(p)? Untuk menyelesaikan ini, perhatikanlah plot PACF sampel. Berdasarkan plot PACF sampel, kita hanya memiliki satu interpretasi, yakni ia berhenti terpotong setelah lag 2 (it cuts off after lag 2). Oleh karena itu, kita menggunakan interpretasi kedua dari plot ACF sampel dan mengasumsikan bahwa model yang sesuai adalah model AR(2).

Tabel 2 menunjukkan output Minitab untuk model AR (2). Estimasi parameternya yaitu \(\hat{ϕ}_1= 0,27\) dan \(\hat{ϕ}_1=0,42\), dan ternyata signifikan (lihat nilai P).

Tabel 2. Output Minitab untuk model AR(2)

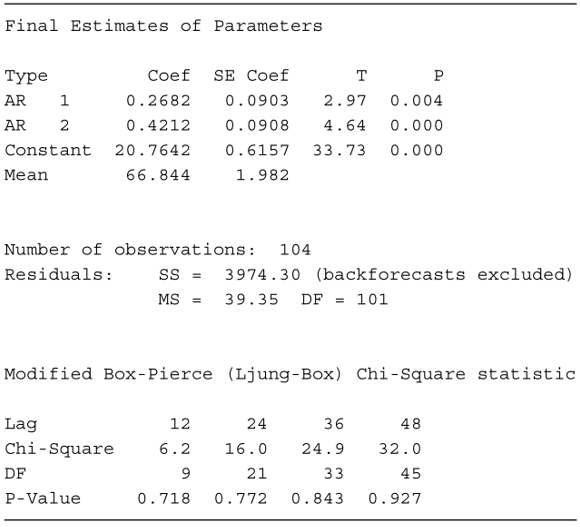
Selain itu, diperoleh nilai MSE sebesar 39,35. Berdasarkan Uji Modified Box-Pierce, tidak ada autokorelasi pada residual. Kita juga bisa melihat hal ini pada plot ACF dan PACF sampel dari residual yang ditunjukkan dalam Gambar 3.

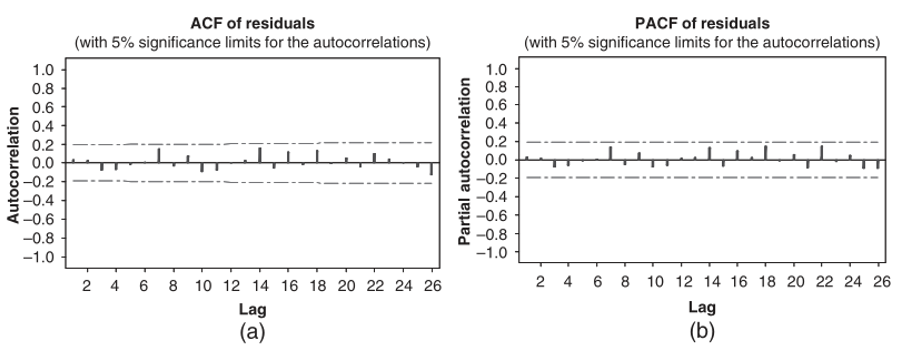
Gambar 3. Plot ACF dan PACF dari residual model

Sebagai pemeriksaan diagnostik terakhir, kita tunjukkan di bawah ini 4 plot yang disediakan Minitab yakni: Normal Probability Plot, Residuals versus Fitted Value, Histogram of the Residuals, and Time Series Plot of the Residuals. Keempat plot ini mengindikasikan bahwa hasil fit (yakni model AR(2)) memang dapat diterima.

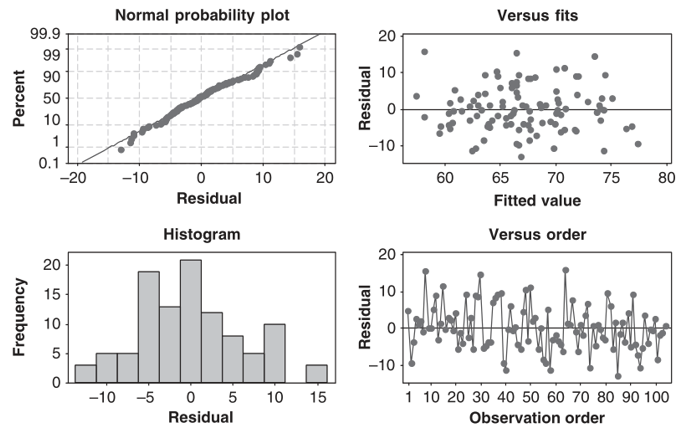
Gambar 4. Plot residual untuk AR(2) berdasarkan data pada Tabel 2.

Sekarang perhatikan Gambar 5 di bawah yang menunjukkan data aktual dan nilai fit berdasarkan model AR(2). Tampak bahwa nilai fit memuluskan data aktual yang tinggi dan rendah (smooth out the highs and lows in the data).

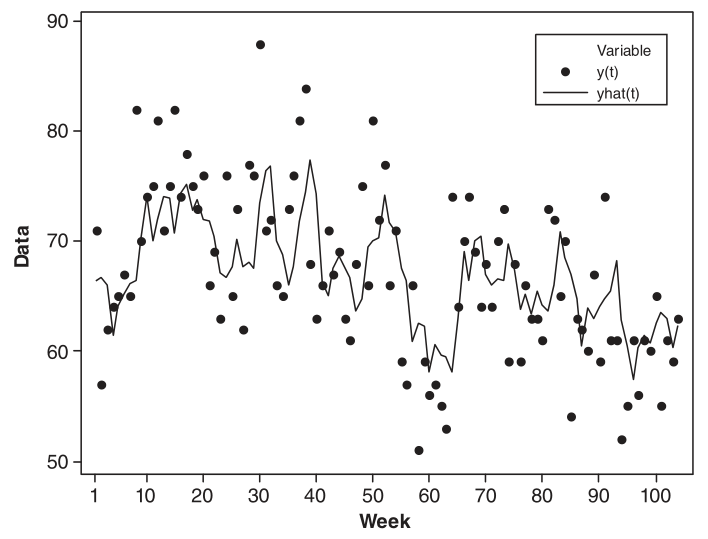
Gambar 5. Plot time series dari data aktual dan nilai fit model AR(2)