Analisis Time Series   »   Konsep Dasar Time Series   ›  Fungsi Autokorelasi (Autocorrelation Function)

Autokorelasi

Fungsi Autokorelasi (Autocorrelation Function)

Dalam analisis time series, terdapat dua konsep penting yang dikenal dengan fungsi autokorelasi (autocorrelation function, ACF) dan fungsi autokorelasi parsial (partial autocorrelation function, PACF). Kedua jenis korelasi tersebut biasanya digunakan dalam spesifikasi model.

---

Dalam analisis time series, terdapat dua konsep penting yang dikenal dengan fungsi autokorelasi (autocorrelation function, ACF) dan fungsi autokorelasi parsial (partial autocorrelation function, PACF). Kedua jenis korelasi tersebut biasanya digunakan dalam spesifikasi model.

Selain itu, ACF juga digunakan untuk mengecek stasioneritas data time series. Akan tetapi, penggunakan ACF dan PACF untuk spesifikasi model dan pengecekan stasioneritas akan dibahas pada artikel tersendiri.

Pada artikel ini, kita hanya akan membahas fungsi autokorelasi dan bagaimana penghitungannya secara manual. Sekarang perhatikan plot untuk data penjualan produk farmasi yang ditunjukkan pada Gambar 1 (sebelah kiri) berikut:

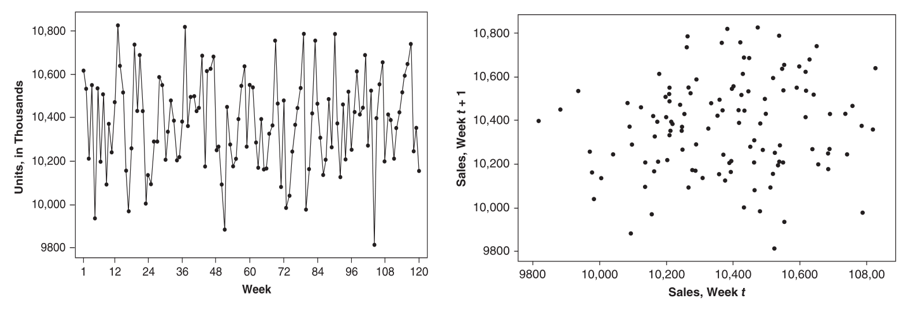
Gambar 1. Plot dan diagram pencar data penjualan produk farmasi

Gambar 1 di atas (sebelah kanan) menunjukkan diagram pencar dari data penjualan produk farmasi (pharmaceutical product sales) untuk lag k = 1. Diagram pencar ini diperoleh dengan memplotkan \(y_{t+1}\) dengan \(y_t\). Dari diagram pencar tersebut tidak tampak adanya pola terstruktur atau pasangan observasi yang berdekatan yakni \(y_t, y_{t+1}\) tampak tidak berkorelasi.

Dengan kata lain, nilai y pada periode sekarang tidak memberikan informasi yang bermanfaat mengenai nilai y yang akan diobservasi pada periode selanjutnya.

Hasil yang berbeda ditunjukkan pada Gambar 2 (sebelah kanan) yang menunjukkan diagram pencar dari data pembacaan viskositas kimia (chemical viscosity readings) untuk lag k = 1.

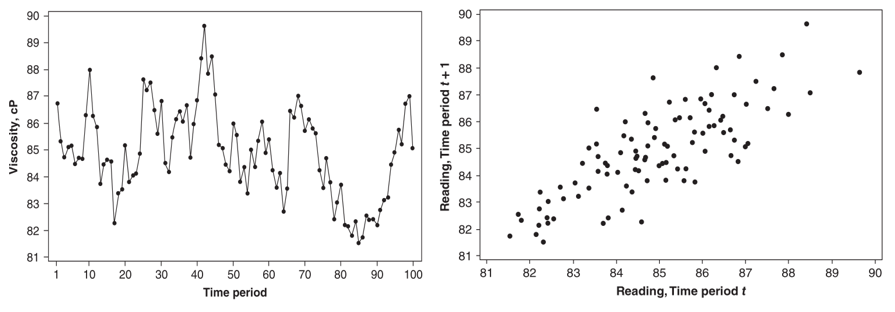
Gambar 2. Plot dan diagram pencar data chemical viscosity readings

Sama seperti pada Gambar 1, diagram pencar pada Gambar 2 diperoleh dengan memplotkan \(y_{t+1}\) dengan \(y_t\). Dari diagram pencar tersebut terlihat bahwa pasangan observasi yang berdekatan yakni \(y_t, y_{t+1}\) berkorelasi positif.

Dengan kata lain, nilai y yang kecil pada periode sekarang cenderung diikuti oleh nilai y yang juga kecil pada periode berikutnya. Begitu pula dengan nilai y yang besar pada periode sekarang cenderung diikuti oleh nilai y yang besar pada periode selanjutnya.

Kovarian antara \(y_t\) dan nilainya pada periode selanjutnya, katakanlah \(y_{t+k}\), disebut autokovarian (autocovariance) pada lag k, dan didefinisikan sebagai:

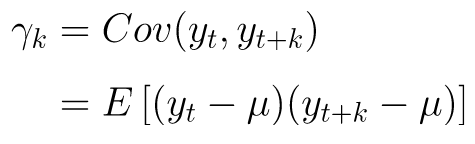
Kumpulan nilai \(γ_k, k=0,1,2,…\) disebut fungsi autokovarian (autocovariance function). Perhatikan bahwa autokovarian pada lag k = 0 sama dengan varians data time series, yakni \(γ_0 = σ_y^2\), yang bernilai konstan untuk data time series stasioner.

Selanjutnya, koefisien autokorelasi (autocorrelation coefficient) pada lag k untuk data time series stasioner yaitu:

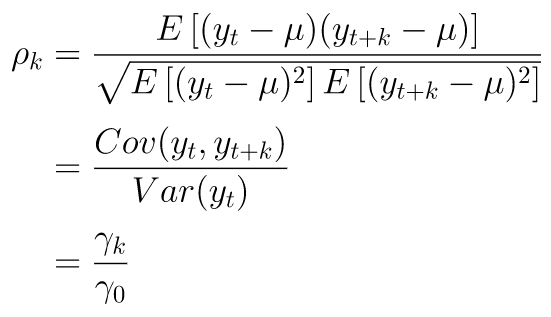
Kumpulan nilai \(ρ_k, k=0,1,2,…\) disebut fungsi autokorelasi (autocorrelation function, ACF). Perhatikan bahwa sesuai definisi, \(ρ_0 = 1\).

Sekarang mari kita estimasi nilai autokovarians dan ACF dari data time series dengan sampel sebanyak T, yakni \(y_1,y_2,…,y_T\). Estimasi fungsi autokovariansnya dapat dirumuskan sebagai berikut:

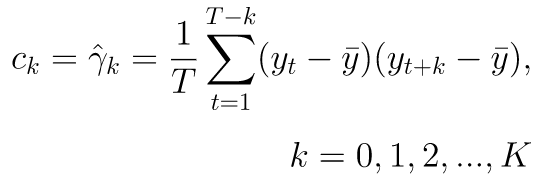
Sementara itu, ACF dapat diestimasi melalui fungsi autokorelasi sampel (sampel ACF) yakni:

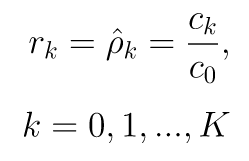
Sebagai aturan sederhana (rule of thumb), diperlukan setidaknya 50 observasi untuk memberikan estimasi ACF yang reliable, dan autokorelasi sampel seharusnya dihitung sampai lag K, di mana K kira-kira sama dengan T/4.

Contoh 1:

Perhatikan data Chemical Process Viscosity Readings pada Tabel 1 di bawah yang mana grafiknya dapat dilihat pada Gambar 2 di atas.

Tabel 1. Data chemical process viscosity readings

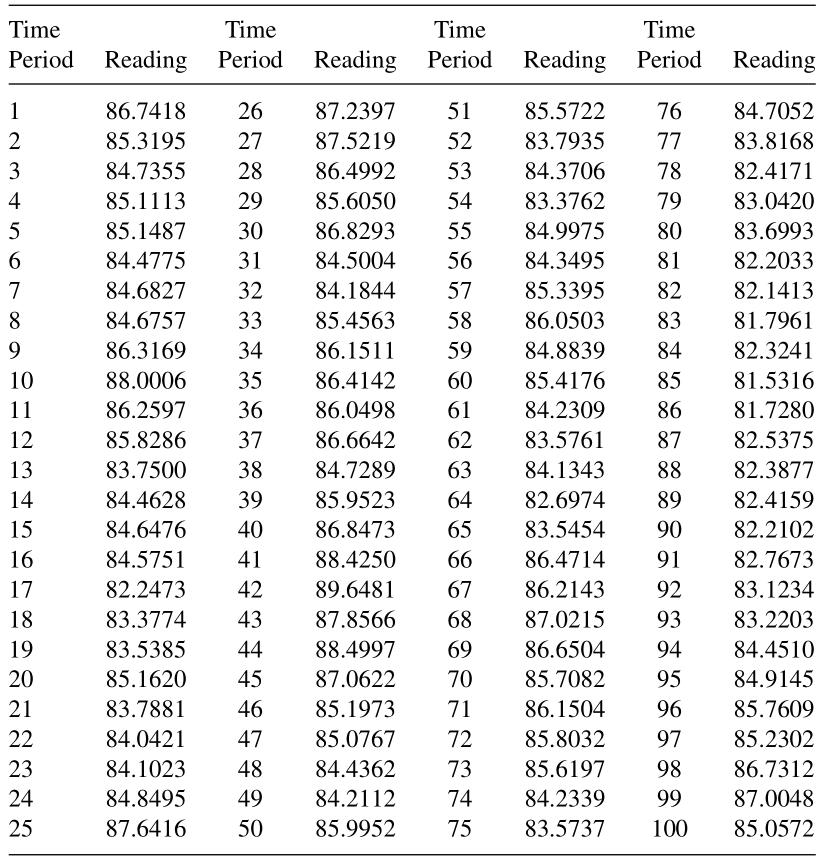
ACF sampel pada lag k dapat dihitung sebagai berikut:

Penghitungan ACF sampel untuk 25 lag pertama diberikan pada Tabel 2 di bawah dan plotnya diberikan pada Gambar 3.

Tabel 2. Hasil penghitungan ACF sampel untuk 25 lag pertama berdasarkan data pada Tabel 1.

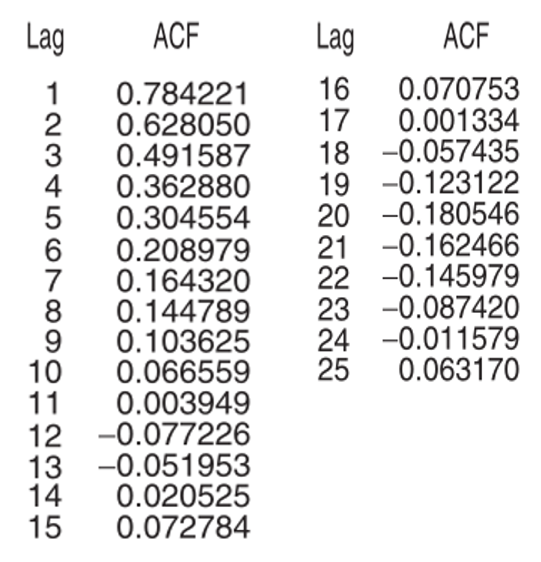
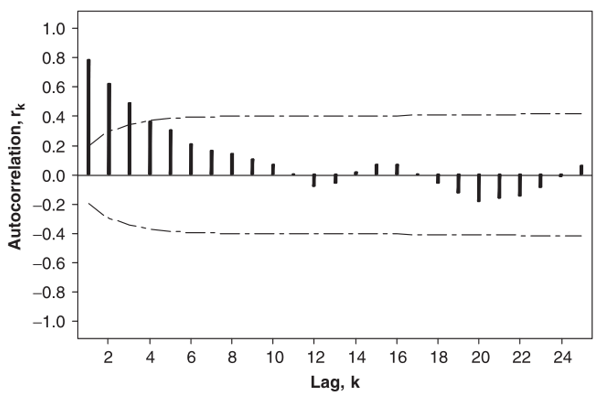
Gambar 3. Plot ACF sampel berdasarkan data pada Tabel 1.