
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Bahas Soal Matematika » Integral › 20 Contoh Soal Integral Fungsi Rasional dan Pembahasannya
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552
20 Contoh Soal Integral Fungsi Rasional dan Pembahasannya
Pada artikel ini kita akan membahas cara mencari integral dari suatu fungsi rasional. Sesuai definisi, fungsi rasional merupakan fungsi yang diperoleh dari hasil bagi antara dua fungsi suku banyak (polinomial) atau bisa dituliskan sebagai berikut:
\[ f(x) = \frac{p(x)}{q(x)}, \quad q(x) \neq 0 \]
di mana \(p(x)\) dan \(q(x)\) merupakan fungsi suku banyak.
Fungsi rasional dapat dibedakan menjadi dua, yaitu fungsi rasional sejati dan fungsi rasional tidak sejati. Disebut fungsi rasional sejati jika derajat atau pangkat polinom pembilang \((p(x))\) lebih kecil daripada derajat polinom penyebut \((q(x))\). Sebaliknya, dikatakan fungsi rasional tidak sejati jika pangkat polinom pembilang lebih besar daripada pangkat polinom penyebutnya. Fungsi rasional tidak sejati dapat dituliskan menjadi:
\[ f(x) = H(x) + \frac{s(x)}{q(x)}, \quad q(x) \neq 0 \]
di mana \(H(x)\) menyatakan hasil bagi polinom, \(s(x)\) adalah sisa pembagian dengan pangkat polinom lebih kecil dari pangkat polinom \(q(x)\).
Berdasarkan penjelasan di atas, maka penyelesaian integral fungsi rasional terdiri dari dua, yakni penyelesaian integral fungsi rasional tidak sejati dan penyelesaian integral fungsi rasional sejati. Untuk integral fungsi rasional tidak sejati, penyelesaiannya bisa dengan melakukan pembagian polinomial terlebih dahulu untuk mendapatkan hasil bagi polinom dan sisanya kemudian selesaikan integralnya.
Untuk integral fungsi rasional sejati, maka penyelesaiannya akan sangat bergantung pada faktor penyebut dari fungsi tersebut. Ada beberapa faktor penyebut, antara lain:
- Faktor linear tunggal
- Faktor linear berulang
- Faktor linear berlainan atau berbeda
- Faktor kuadrat tunggal
- Faktor kuadrat berulang
- Faktor kuadrat berlainan atau berbeda
- Kombinasi dari beberapa faktor di atas

Contoh soal dan pembahasan
Supaya kamu lebih paham dengan penjelasan di atas, mari kita bahas beberapa contoh soal terkait integral fungsi rasional berikut ini. Di sini telah disiapkan sebanyak 20 contoh soal disertai dengan pembahasannya. Jika dari pembahasan soal ada yang kurang jelas silahkan tanyakan di kolom komentar di bawah artikel ini. Ingat, malu bertanya sesat di jalan. Semoga kamu yang membaca artikel ini tidak tersesat.
Contoh 1:
Tentukan hasil dari \( \int \frac{x^2}{x-2} \ dx = \cdots \)
Pembahasan:
Perhatikan bahwa fungsi dalam integral (integran) memiliki pembilang dengan pangkat yang lebih besar dari penyebut sehingga kita bisa melakukan pembagian pembilang oleh penyebut terlebih dahulu. Ini bertujuan untuk menyederhanakan fungsi tersebut sehingga dapat diintegralkan dengan mudah.
Berikut hasil yang diperoleh:
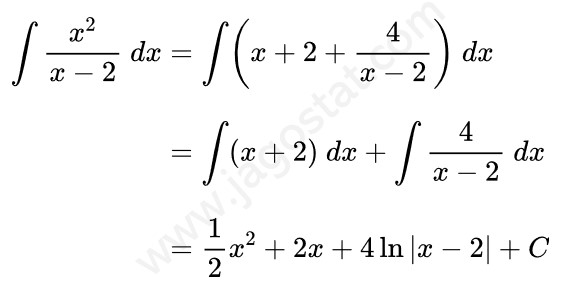
Contoh 2:
Tentukan hasil dari \( \int \frac{x^2}{3x-3} \ dx = \cdots \)
Pembahasan:

Contoh 3:
Tentukan hasil dari \( \int \frac{x^5+2x^3-x+1}{x^3+5x} \ dx = \cdots \)
Pembahasan:
Perhatikan bahwa fungsi dalam integralnya merupakan fungsi rasional tidak sejati di mana pangkat pembilang polinom lebih besar dari pangkat penyebut sehingga dilakukan pembagian polinom terlebih dahulu, diperoleh:
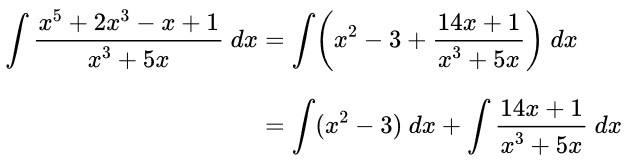
Dari hasil di atas, untuk integral yang pertama dapat dikerjakan dengan rumus dasar integral, yakni:

Selanjutnya, untuk integral yang kedua, fungsi dalam integralnya merupakan fungsi rasional sejati di mana pangkat pembilang lebih kecil dari pangkat penyebut. Fungsi pada penyebut dapat diuraikan menjadi faktor linear yang berlainan, yaitu:

Sekarang kita akan mencari nilai A, B, dan C, yakni:

Dari hasil di atas diperoleh nilai \( A = \frac{1}{5}, \ B = -\frac{1}{5} \) dan \(C = 14\) sehingga

Dengan demikian, hasil dari \( \int \frac{x^5+2x^3-x+1}{x^3+5x} \ dx \) adalah

Baca juga:
Contoh 4:
Tentukan hasil dari \( \int \frac{x^5-3}{x^3-x} \ dx = \cdots \)
Pembahasan:
Perhatikan bahwa fungsi dalam integralnya merupakan fungsi rasional tidak sejati di mana pangkat pembilang polinom lebih besar dari pangkat penyebut sehingga dilakukan pembagian polinom terlebih dahulu, diperoleh:

Dari hasil di atas, untuk integral yang pertama dapat dikerjakan dengan rumus dasar integral, yakni:
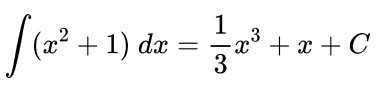
Selanjutnya, untuk integral yang kedua, fungsi dalam integralnya merupakan fungsi rasional sejati di mana pangkat pembilang lebih kecil dari pangkat penyebut. Fungsi pada penyebut dapat diuraikan menjadi faktor linear yang berlainan, yaitu:
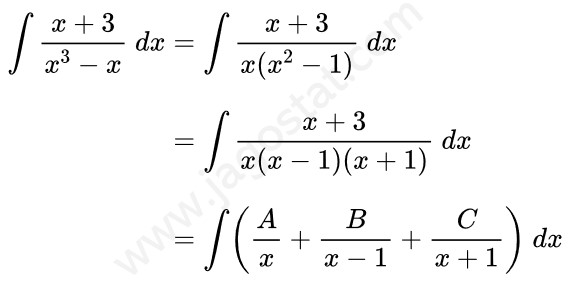
Sekarang kita akan mencari nilai A, B, dan C sebagai berikut:
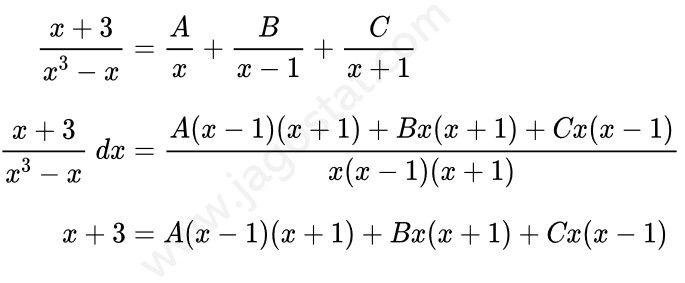
Dari hasil di atas, kita akan mengambil sembarang nilai \(x = -1, 0, 1 \) untuk memperoleh nilai A, B, dan C.

Dengan demikian, diperoleh:

Jadi, hasil dari \( \int \frac{x^5-3}{x^3-x} \ dx \) adalah

Contoh 5:
Tentukan hasil dari \( \displaystyle \int \frac{5x+3}{x^2-9} \ dx = \cdots \)
Pembahasan:
Fungsi penyebut pada integran jika diuraikan mengandung faktor linear yang berlainan. Perhatikan hasil berikut:

Selanjutnya, akan dicari nilai A dan B, yaitu sebagai berikut:

Dari hasil di atas diperoleh nilai \(A = 3\) dan \(B=2\) sehingga kita dapatkan hasil berikut:
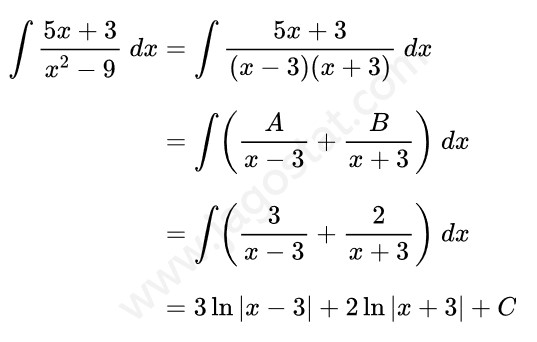
Contoh 6:
Tentukan hasil dari \( \int \frac{x+1}{x^2-2x+1} \ dx = \cdots \)
Pembahasan:
Perhatikan bahwa fungsi penyebut pada integran mengandung faktor linear yang berulang sehingga bisa dituliskan menjadi:

Selanjutnya, kita akan mencari nilai A dan B, yakni:

Dari hasil di atas diperoleh nilai \( A = 1 \) dan \(B=2\). Dengan demikian,

Contoh 7:
Tentukan hasil dari \( \displaystyle \int \frac{2x+1}{x^2-3x+2} \ dx \).
Pembahasan:
Perhatikan bahwa fungsi penyebut pada integran mengandung faktor linear yang berlainan sehingga bentuk integralnya bisa dituliskan menjadi:

Sekarang kita akan mencari nilai A dan B menggunakan kesamaan polinom berikut:
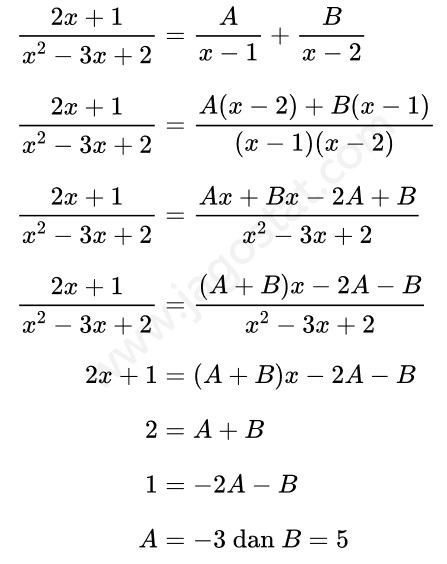
Dari hasil di atas diperoleh nilai \(A = -3\) dan \(B = 5\). Dengan demikian,
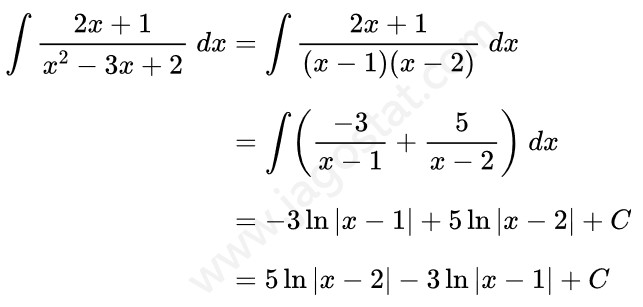
Contoh 8:
Tentukan hasil dari \( \displaystyle \int \frac{3x-13}{x^2+3x-10} \ dx = \cdots \)
Pembahasan:
Fungsi penyebut pada integran mengandung faktor linear yang berlainan sehingga bentuk integralnya bisa diubah menjadi:

Selanjutnya adalah mencari nilai \(A\) dan \(B\). Perhatikan berikut ini:

Berdasarkan persamaan di atas, diperoleh hubungan antara A dan B sebagai berikut:
\begin{aligned} A+B &= 3 \\[8pt] 2A-5B &= 13 \end{aligned}
Dengan menyelesaikan SPLDV di atas diperoleh nilai \(A = 4\) dan \(B=-1\). Dengan demikian,
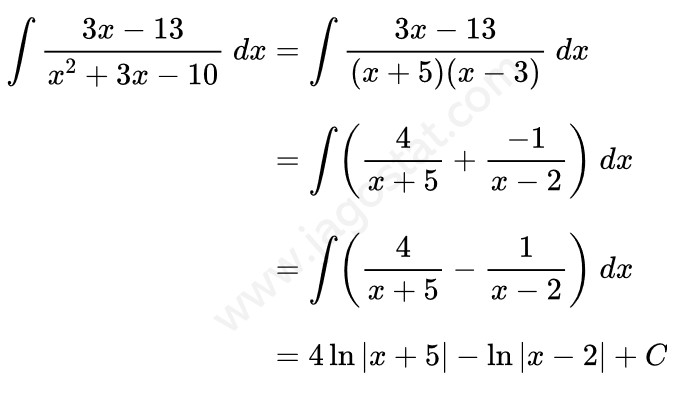
Contoh 9:
Tentukan hasil dari \( \displaystyle \int \frac{1}{4x^2-9} \ dx \)
Pembahasan:
Fungsi penyebut pada integran mengandung faktor linear yang berlainan sehingga bentuk integralnya bisa diubah menjadi:

Selanjutnya adalah mencari nilai \(A\) dan \(B\). Perhatikan berikut ini:

Dari persamaan di atas, diperoleh hubungan antara A dan B sebagai berikut:
\begin{aligned} 2A+2B &= 0 \\[8pt] -3A+3B &= 1 \end{aligned}
Dengan menyelesaikan hasil di atas, diperoleh nilai \(A = -\frac{1}{6} \) dan \(B=\frac{1}{6} \). Dengan demikian,
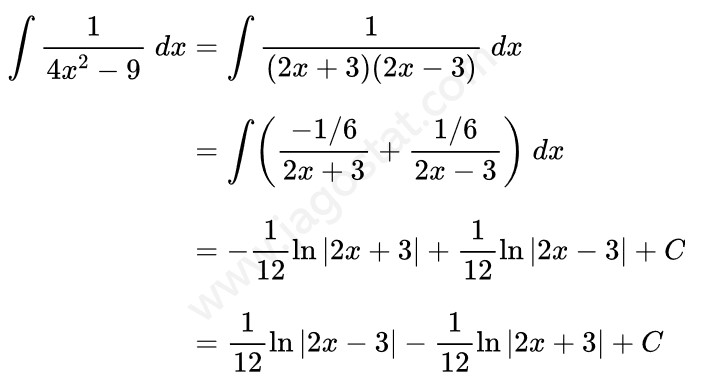
Baca juga:
Contoh 10:
Tentukan hasil dari \( \displaystyle \int \frac{x-3}{x^3-x} \ dx = \cdots \)
Pembahasan:
Perhatikan bahwa fungsi penyebut dalam integran mengandung faktor linear yang berlainan, yakni:

Kita peroleh berikut ini:

Untuk menyelesaikan integral di atas, kita perlu mencari nilai A, B, dan C terlebih dahulu. Perhatikan berikut ini:
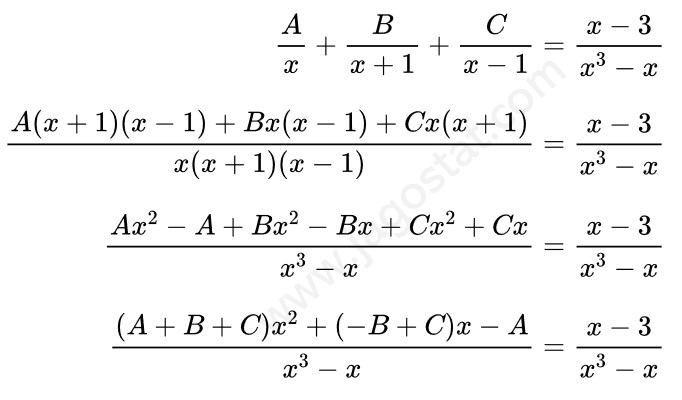
Dari persamaan di atas, diperoleh hubungan:
\begin{aligned} A+B+C &= 0 \\[8pt] -B+C &= 1 \\[8pt] A &= 3 \end{aligned}
Dengan menyelesaikan hasil di atas, diperoleh nilai \( A = 3, \ B = -2 \) dan \( C = -1 \). Dengan demikian,

Contoh 11:
Tentukan hasil dari \( \displaystyle \int \frac{x+4}{x^3-4x^2+4x} \ dx = \cdots \)
Pembahasan:
Perhatikan bahwa fungsi penyebut dalam integran mengandung faktor linear berulang, yakni:
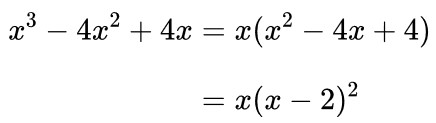
Kita peroleh berikut ini:
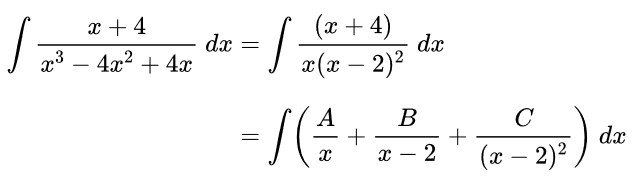
Untuk menyelesaikan integral di atas, kita perlu mencari nilai A, B, dan C terlebih dahulu. Perhatikan berikut ini:

Dari persamaan di atas, diperoleh hubungan sebagai berikut:
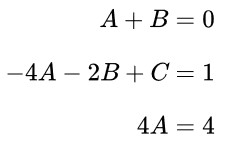
Dengan menyelesaikan hasil di atas, diperoleh nilai \( A = 1, \ B = -1 \) dan \( C = 3 \). Dengan demikian,

Contoh 12:
Tentukan hasil dari \( \displaystyle \int \frac{2x+1}{x^3-7x+6} \ dx = \cdots \)
Pembahasan:
Perhatikan bahwa fungsi penyebut pada integral mengandung faktor linear berlainan sehingga bentuk integralnya bisa dituliskan menjadi:
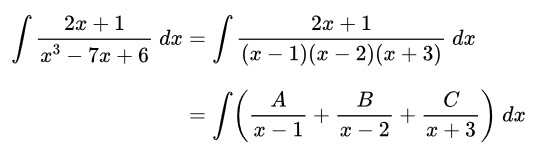
Sekarang kita akan mencari nilai A, B dan C, yakni

Dari hasil di atas, untuk \( x = 1, 2, \) dan 3, diperoleh hasil sebagai berikut:

Jadi diperoleh nilai \( A = -\frac{3}{4}, \ B = 1 \) dan \( C = -\frac{1}{4} \). Dengan demikian,
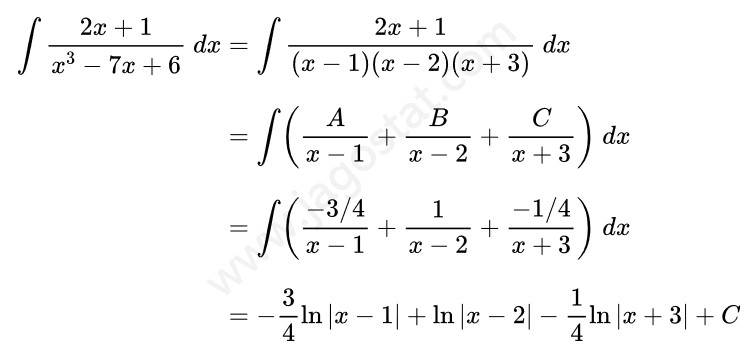
Contoh 13:
Tentukan hasil dari \( \displaystyle \int \frac{x}{(x-2)^2(x+4)} \ dx \)
Pembahasan:
Fungsi penyebut pada integral mengandung faktor linear yang berulang sehingga bisa dituliskan menjadi:
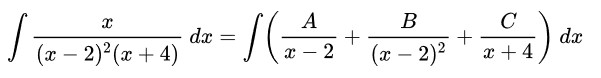
Selanjutnya, cari nilai A dan B, yakni:

Dari hasil di atas, untuk \(x = 2\), maka diperoleh:
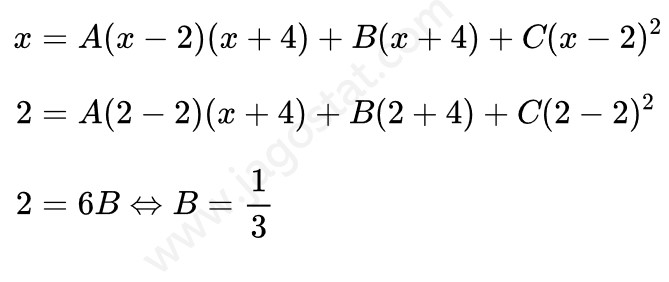
Dan untuk \(x=-4\) dan \(x=0\), diperoleh:

Jadi, berdasarkan hasil yang telah didapatkan di atas, diperoleh nilai \( A = \frac{1}{9}, \ B = \frac{1}{3} \) dan \( C = -\frac{1}{9} \). Dengan demikian,

Contoh 14:
Tentukan hasil dari \( \int \frac{3x^2-8x+13}{(x+3)(x-1)^2} \ dx = \cdots \)
Pembahasan:
Fungsi penyebut pada integran mengandung faktor linear yang berulang sehingga bisa dituliskan menjadi:
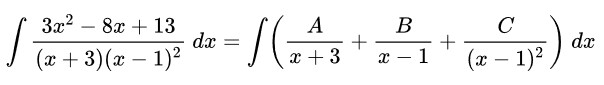
Sekarang kita akan mencari nilai A, B, dan C, yakni sebagai berikut:
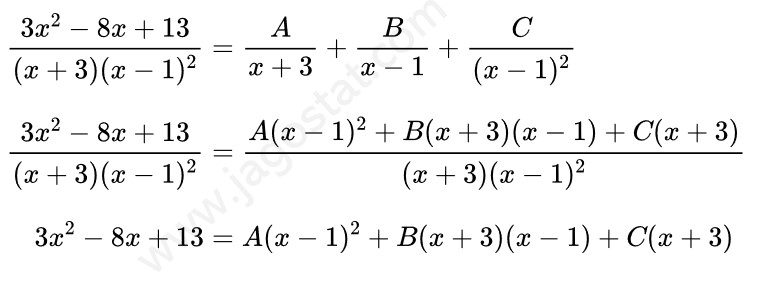
Dari hasil di atas, untuk \( x = -3, 1, 0 \) maka diperoleh:

Jadi diperoleh nilai \(A = 4, \ B = -1\) dan \(C = 2\). Dengan demikian, kita dapatkan hasil sebagai berikut:

Contoh 15:
Tentukan hasil dari \( \int \frac{dx}{x^3+x} \ dx = \cdots \)
Pembahasan:
Fungsi penyebut pada integran dapat diuraikan menjadi faktor linear dan faktor kuadrat. Perhatikan hasil berikut:

Sekarang akan dicari nilai A, B, dan C, yakni:

Berdasarkan hasil di atas diperoleh nilai \(A = 1, B = -1\), dan \(C = 0\). Dengan demikian, kita dapatkan berikut ini:
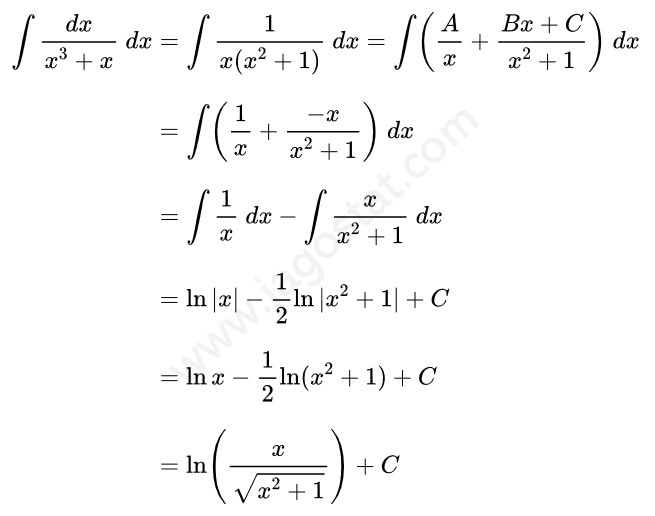
Baca juga:
Contoh 16:
Tentukan hasil dari \( \displaystyle \int \frac{2x^2-3x-36}{(2x-1)(x^2+9)} \ dx = \cdots \)
Pembahasan:
Perhatikan bahwa fungsi penyebut pada integran mengadung faktor kuadrat tunggal sehingga bentuk integralnya bisa ditulis menjadi:

Setelah itu, tugas kita sekarang adalah mencari nilai A, B, dan C. Perhatikan berikut ini:

Berdasarkan persamaan di atas, diperoleh nilai \( A = -4, \ B = 3 \) dan \( C = 0 \). Dengan demikian,
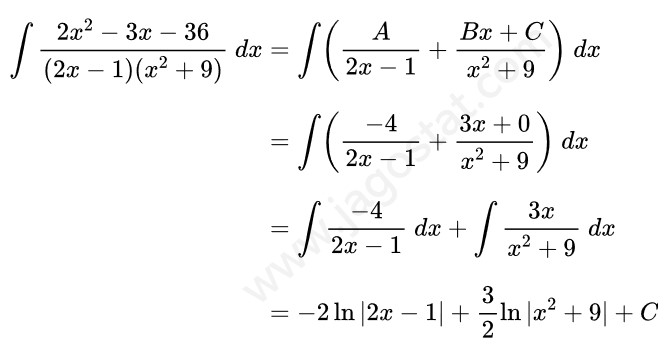
Contoh 17:
Tentukan hasil dari \( \displaystyle \int \frac{2x+6}{(x^2+3)(x^2+1)} \ dx \)
Pembahasan:
Fungsi penyebut pada integran mengandung faktor kuadrat yang berlainan sehingga bentuk integralnya bisa dituliskan menjadi:
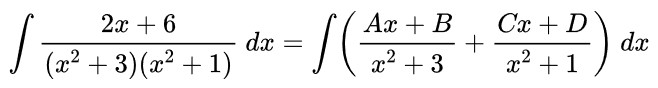
Selanjutnya cari nilai A, B, C, dan D, yakni:

Berdasarkan nilai A, B, C, dan D yang diperoleh di atas, maka kita dapatkan hasil sebagai berikut:

Contoh 18:
Tentukan hasil dari \( \int \frac{x^3+x-1}{(x^2+1)^2} \ dx = \cdots \)
Pembahasan:
Perhatikan bahwa fungsi penyebut pada integran mengandung faktor kuadrat berulang, sehingga bisa dituliskan:

Sekarang kita akan mencari nilai A, B, C, dan D, yakni:

Berdasarkan nilai \( A, B, C, \) dan \(D\) yang diperoleh di atas, kita dapatkan hasil berikut ini:

Contoh 19:
Tentukan hasil dari \( \int \frac{3x^3-2x^2+5x-1}{(x-2)(x^2+1)^2} \ dx = \cdots \)
Pembahasan:
Fungsi penyebut pada integran mengandung faktor linear dan faktor kuadrat berulang, sehingga bisa diperoleh:

Selanjutnya, cari nilai A, B, dan C yakni sebagai berikut:

Nilai A, B, C, D, dan E yang memenuhi hubungan di atas adalah \( A = 1, B = -1, C = 1, D = -1 \) dan \( E = 0 \). Dengan demikian, diperoleh:

Contoh 20:
Tentukan hasil dari \( \displaystyle \int \frac{2x^3+x^2+2x-1}{x^4-1} \ dx = \cdots \)
Pembahasan:
Fungsi penyebut dalam integran bisa diuraikan sebagai berikut:

Perhatikan bahwa bentuk penyebut setelah diuraikan mengandung faktor linear berlainan dan faktor kuadrat tunggal sehingga bisa dituliskan menjadi:

Sekarang kita akan mencari nilai dari A, B, C, dan D menggunakan kesamaan polinom berikut:

Dari hasil di atas diperoleh hubungan sebagai berikut:

Nilai A, B, C, dan D yang memenuhi hubungan di atas adalah \(A=B=D=1\) dan \(C = 0\). Dengan demikian,

Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan jika ada yang kurang jelas dari pembahasan artikel ini silahkan tanyakan di kolom komentar.
Artikel terkait
Inside of every problem lies an opportunity.
