Contoh Soal dan Pembahasan Pertidaksamaan Akar Matematika SMA

Bahas Soal Matematika » Pertidaksamaan › Contoh Soal dan Pembahasan Pertidaksamaan Akar Matematika SMA

Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552

Contoh Soal dan Pembahasan Pertidaksamaan Akar Matematika SMA

Kita telah membahas beberapa bentuk pertidaksamaan pada artikel lain. Kita tahu bahwa suatu bentuk pertidaksamaan matematika dapat berupa linear, kuadrat, pecahan, akar, nilai mutlak, eksponen, maupun logaritma.

Pada artikel ini, kita akan membahas cara menyelesaikan atau mengerjakan soal-soal pertidaksamaan yang berbentuk akar. Soal pertidaksamaan akar ini biasanya sering muncul dalam soal ujian nasional maupun soal ujian masuk perguruan tinggi.

Contoh 1: SBMPTN 2014

Semua nilai \(x\) yang memenuhi \( \sqrt{x+10} - \sqrt{x+2} > 2 \) adalah…

\( -2 \leq x < -1 \)
\( x > 1 \)
\( -\frac{3}{2} \leq x < -1 \)
\( x > 2 \)
\( -1 < x < 6 \)

Pembahasan »

Untuk menyelesaikan pertidaksamaan bentuk akar di atas, ada beberapa langkah yang perlu kita lakukan.

Langkah pertama: Selesaikan pertidaksamaan bentuk akar tersebut dengan menyamakan ruas kiri dan kanan, kemudian dikuadratkan. Kita peroleh berikut ini:

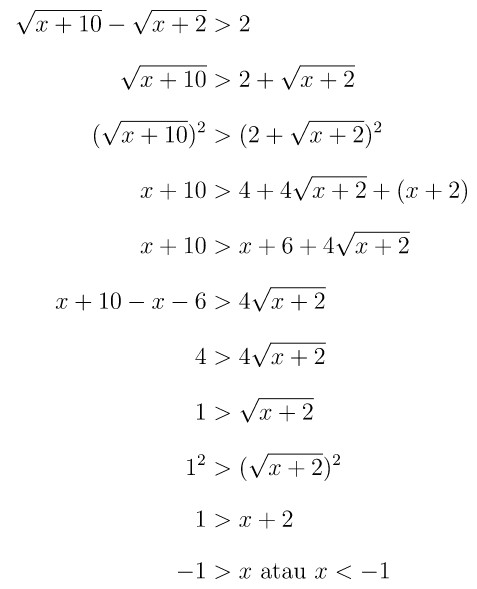
Langkah kedua: Carilah nilai \(x\) yang memenuhi atau membuat \( \sqrt{x+10} \) terdefinisi. Agar \( \sqrt{x+10} \) terdefinisi maka nilai \(x\) yang memenuhi, yaitu:

\begin{aligned} x+10 &\geq 0 \\[8pt] x &\geq -10 \end{aligned}

Langkah ketiga: Lakukan hal yang sama seperti pada Langkah Kedua di atas untuk mencari nilai \(x\) yang memenuhi atau membuat \( \sqrt{x+2} \) terdefinisi. Kita peroleh berikut ini:

\begin{aligned} x+2 &\geq 0 \\[8pt] x &\geq -2 \end{aligned}

Irisan ketiga nilai \(x\) yang memenuhi pada pertidaksamaan di atas adalah himpunan penyelesaian dari pertidaksamaan bentuk akar yang diberikan dalam soal ini. Jika digambarkan, kita peroleh berikut ini:

Dari gambar di atas, himpunan penyelesaiannya adalah \( -2 \leq x < -1 \).

Jawaban A.

Contoh 2: UM UGM 2019

Jika himpunan penyelesaian untuk pertidaksamaan \( \sqrt{x^2-x+1} \leq \sqrt{x+1} \) adalah \( \{ x|x \ \text{bilangan real}, \ a \leq x \leq b \} \), maka \(a + b = \cdots \)

\( 1 \)
\( 2 \)
\( 3 \)
\( 4 \)
\( 5 \)

Pembahasan »

Untuk menyelesaikan pertidaksamaan bentuk akar di atas, ada beberapa langkah yang perlu dilakukan.

Langkah pertama: Kita selesaikan pertidaksamaan dengan mengkuadratkan ruas kiri dan kanan pertidaksamaan akar tersebut. Perhatikan berikut ini:

Dari hasil di atas kita peroleh himpunan penyelesaian pertidaksamaan tersebut adalah \( 0 \leq x \leq 2 \).

Langkah kedua: Carilah nilai \(x\) yang memenuhi \( \sqrt{x^2-x+1} \). Ingat bahwa agar \( \sqrt{x^2-x+1} \) mempunyai nilai real, maka \( x^2-x+1 \geq 0 \). Karena \(a > 0\) da \( D = b^2-4ac < 0 \) maka \( x^2-x+1 \) definit positif yang artinya selalu bernilai positif untuk setiap \(x\) bilangan real. Dengan demikian, nilai \(x\) yang memenuhi \( x^2-x+1 \geq 0\) adalah \( x \in R\).

Langkah ketiga: Lakukan hal yang sama seperti pada Langkah Kedua di atas untuk mencari nilai \(x\) yang memenuhi atau membuat \( \sqrt{x+1} \) terdefinisi. Agar \(\sqrt{x+1}\) terdefinisi maka \( x+1 \geq 0 \). Perhatikan berikut ini:

\begin{aligned} x+1 &\geq 0 \\[8pt] x &\geq -1 \end{aligned}

Dari ketiga langkah di atas, irisan nilai \(x\) yang memenuhi pada pertidaksamaan akar di atas merupakan himpunan penyelesaian dari pertidaksamaan tersebut. Jika digambarkan kurang lebih seperti berikut ini:

Dari gambar di atas, himpunan penyelesaiannya adalah \( 0 \leq x \leq 2 \) dan \( a \leq x \leq b \) sehingga \( a = 0 \) dan \(b=2\). Nilai \(a+b = 2\).

Jawaban B.

Baca juga:

Bentuk akar dan sifat-sifatnya

Contoh 3: SBMPTN 2014

Himpunan penyelesaian pertidaksamaan \( \sqrt{x^2-2x} < \sqrt{3x+6} \) adalah…

\( \{ x | -1 < x < 6 \} \)
\( \{ x | -2 \leq x < 0 \ \text{atau} \ x \geq 2 \} \)
\( \{ x | x \geq -2 \} \)
\( \{ x | -2 \leq x \leq 0 \ \text{atau} \ 2 \leq x < 6 \} \)
\( \{ x | -1 < x \leq 0 \ \text{atau} \ 2 \leq x < 6 \} \)

Pembahasan »

Untuk menyelesaikan pertidaksamaan bentuk akar dalam soal ini, ada beberapa tahapan yang perlu diperiksa.

Pertama, kita coba selesaikan pertidaksamaan dengan mengkuadratkan ruas kiri dan kanan pertidaksamaan tersebut, yakni:

Dari hasil di atas diperoleh himpunan penyelesaian pertidaksamaan kuadratnya adalah \( -1 < x < 6 \).

Kedua, tentukan nilai \(x\) agar bentuk akar \( \sqrt{x^2-2x} \) terdefinisi atau mempunyai nilai real. Agar \( \sqrt{x^2-2x} \) mempunyai nilai real, maka syaratnya adalah:

\begin{aligned} x^2-2x &\geq 0 \\[8pt] x(x-2) &\geq 0 \\[8pt] x = 0 \ &\text{atau} \ x = 2 \\[8pt] \text{HP:} \ \{ x \ | \ x \leq 0 \ &\text{atau} \ x \geq 2 \} \end{aligned}

Ketiga, sama seperti pada tahap kedua di atas, tentukan nilai \(x\) agar bentuk akar \( \sqrt{3x+6} \) mempunyai nilai real.

\begin{aligned} 3x+6 &\geq 0 \\[8pt] 3x &\geq -6 \\[8pt] x &\geq -2 \end{aligned}

Dari ketiga tahapan penyelesaian di atas, irisan dari ketiga nilai \(x\) yang diperoleh adalah himpunan penyelesaian pertidaksamaan akar yang diberikan dalam soal. Jika digambarkan hasilnya kurang lebih seperti berikut:

Dari gambar di atas, himpunan penyelesaiannya adalah \( HP: \{ x | -1 < x \leq 0 \ \text{atau} \ 2 \leq x < 6 \} \).

Jawaban E.

Contoh 4: UMB-PT 2014

Solusi pertidaksamaan \( \sqrt{3-x} \leq x-1 \) adalah himpunan semua bilangan real \(x\) yang memenuhi…

\( -1 \leq x \leq 2 \)
\( x \leq -1 \ \text{atau} \ 2 \leq x \leq 3 \)
\( 1 \leq x \leq 2 \)
\( x \leq -1 \ \text{atau} \ x \geq 2 \)
\( 2 \leq x \leq 3 \)

Pembahasan »

Untuk menyelesaikan pertidaksamaan bentuk akar di atas, ada beberapa tahapan yang perlu diperiksa.

Pertama, kita coba selesaikan pertidaksamaan dengan mengkuadratkan ruas kiri dan kanan pertidaksamaan tersebut. Berikut hasil yang diperoleh:

Dari hasil di atas diperoleh himpunan penyelesaian pertidaksamaan kuadrat di atas adalah \( x \leq -1 \) atau \(x \geq 2\).

Kedua, tentukan nilai \(x\) agar bentuk akar \( \sqrt{3-x} \) terdefinisi atau mempunyai nilai real. Agar \( \sqrt{3-x} \) mempunyai nilai real, maka syaratnya yaitu:

\begin{aligned} 3-x \geq 0 \\[8pt] x-3 \leq 0 \\[8pt] x \leq 3 \end{aligned}

Ketiga, karena \( 3-x \geq 0 \) dan agar \( \sqrt{3-x} \leq x-1 \) mempunyai nilai real, maka syaratnya yaitu \(x-1 \geq 0 \Rightarrow x \geq 1 \).

Dari hasil di atas, himpunan penyelesaiannya adalah \( HP: \{ x | 2 \leq x \leq 3 \} \).

Jawaban E.

Baca juga:

Cara menyelesaikan suatu pertidaksamaan - Materi, contoh soal dan pembahasan

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.