www.jagostat.com

www.jagostat.com

Website Belajar Matematika & Statistika

Website Belajar Matematika & Statistika

Bahas Soal Matematika   »   Pertidaksamaan   ›  Contoh Soal dan Pembahasan Pertidaksamaan Matematika SMA
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552

Contoh Soal dan Pembahasan Pertidaksamaan Matematika SMA


Contoh 1: SNMPTN 2011

Jika \( 2 < x < 4, \ 3 < y < 5 \) dan \( w = x+y \), maka nilai \(w\) berada antara nilai…

  1. 5 dan 7
  2. 4 dan 9
  3. 5 dan 8
  4. 5 dan 9
  5. 4 dan 7
Pembahasan »

Karena yang mau kita cari adalah nilai \( w= x+y\) di mana \( 2 < x < 4 \) dan \( 3 < y < 5 \) maka kita dapat kisaran nilai \(x+y\). Dari \( 2 < x < 4 \) dan \( 3 < y < 5 \), diperoleh:

\begin{array}{rcccl} 2 + 3 & \leq & x+y & \leq & 4+5 \\[8pt] 5 & \leq & x+y & \leq & 9 \end{array}

Jawaban D.

Contoh 2: SBMPTN 2014

Penyelesaian pertidaksamaan \( \displaystyle \left( \frac{x-1}{x} \right)^2 \leq 4 \left( 1-\frac{1}{x} \right)-3 \) adalah...

  1. \( x \leq -\frac{1}{2} \)
  2. \( x \geq -\frac{1}{2} \)
  3. \( x \geq 2 \)
  4. \( x \leq 2 \)
  5. \( x \leq -\frac{1}{2} \) atau \( x \geq 2 \)
Pembahasan »

Jika kita misalkan \( a = \frac{x-1}{x} \), maka diperoleh:

\begin{aligned} \left( \frac{x-1}{x} \right)^2 &\leq 4 \left( 1-\frac{1}{x} \right)-3 \\[8pt] \left( \frac{x-1}{x} \right)^2 &\leq 4 \left( \frac{x-1}{x} \right)-3 \\[8pt] a^2 &\leq 4a-3 \\[8pt] a^2-4a+3 &\leq 0 \\[8pt] (a-1)(a-3) &\leq 0 \\[8pt] HP &=\{ a \ | \ 1 \leq a \leq 3 \} \end{aligned}

Dari hasil di atas diperoleh himpunan penyelesaiannya adalah \( 1 \leq a \leq 3 \) sehingga:

\begin{array}{rcccl} 1 & \leq & a & \leq & 3 \\[8pt] 1 & \leq & \frac{x-1}{x} & \leq & 3 \\[8pt] x & \leq & x-1 & \leq & 3x \\[8pt] x-x & \leq & x-1-x & \leq & 3x-x \\[8pt] 0 & \leq & -1 & \leq & 2x \end{array}

Karena \(0 \leq -1\) tidak memenuhi sehingga himpunan penyelesaian yang memenuhi hanya \(-1 \leq 2x\) atau \( x \geq -\frac{1}{2} \).

Jawaban B.

Contoh 3: UMB-PT 2013

Sebuah partikel bergerak sepanjang sumbu \(t\) dan posisi partikel di setiap saat adalah \( s(t)=2t^3-24t^2+90t+7, \ t \geq 0 \). Kecepatan partikel ini positif bilamana \(t\) memenuhi…

  1. \( 0 \leq t < 3 \) atau \( t > 5 \)
  2. \( 3 < t < 5 \)
  3. \( 0 \leq t < 5 \)
  4. \( t \geq 0 \)
  5. \( t = 0 \) atau \( t = 5 \)
Pembahasan »

Untuk mendapatkan fungsi kecepatan selalu positif dapat kiga gunakan aturan turunan pertama dari fungsi \( s(t) \), di mana \( v(t) = s’(t) = 6t^2-48t+90 \). Nilai kecepatan selalu positif, yang berarti \( v(t) > 0 \) sehingga dapat kita tuliskan:

\begin{aligned} v(t) &> 0 \\[8pt] 6t^2-48t+90 &> 0 \\[8pt] t^2-8t+15 &> 0 \\[8pt] (t-5)(t-3) &> 0 \\[8pt] t < 3 \ \text{atau} \ t &> 5 \end{aligned}

Karena \( t \geq 0 \) maka nilai \(t\) yang memenuhi adalah \( 0 \leq t < 3 \) atau \( t > 5 \).

Jawaban A.

Contoh 4: SBMPTN 2014

Himpunan semua bilangan real \(x\) yang memenuhi \( x^2+\frac{1}{x^2} \leq 2 \) adalah…

  1. \( \{ -1, 1 \} \)
  2. \( \{ x \ | \ -1 \leq x \leq 1, \ x \neq 0 \} \)
  3. \( \{ x \ | \ x \leq -1 \ \text{atau} \ x \geq 1 \} \)
  4. \( \{ x \ | \ 0 < x \leq 1 \} \)
  5. \( \{ x \ | \ -\frac{3}{2} \leq x \leq 1, \ x \neq 0 \} \)
Pembahasan »

Kita bisa buat pertidaksamaan yang diberikan pada soal menjadi bentuk umum pertidaksamaan pecahan, yakni:

\begin{aligned} x^2+\frac{1}{x^2} \leq 2 \Leftrightarrow \frac{x^4+1}{x^2}-2 \leq 0 \\[8pt] \frac{x^4+1-2x^2}{x^2} \leq 0 \\[8pt] \frac{(x^2-1)^2}{x^2} \leq 0 \\[8pt] \left( \frac{x^2-1}{x} \right)^2 \leq 0 \\[8pt] \left( \frac{(x-1)(x+1)}{x} \right)^2 \leq 0 \end{aligned}

Perhatikan bahwa dari hasil di atas untuk setiap nilai \(x\) maka \( \left( \frac{(x-1)(x+1)}{x} \right)^2 \leq 0 \) sehingga nilai \(x\) yang memenuhi hanya ketika \( \frac{(x-1)(x+1)}{x} = 0 \) sehingga diperoleh \(x = -1\) atau \(x = 1\).

Jawaban A.

Contoh 5: UM UGM 2019

Nilai \(x\) yang merupakan penyelesaian dari \( -2^{2x+1}+4^x+8^{x+\frac{1}{3}}-16^{ \frac{2x-1}{4} } > 0 \) adalah…

  1. \( -1 \leq x < 0 \)
  2. \( x > 0 \)
  3. \( x < 0 \) atau \( x > 1\)
  4. \( 0 \leq x < 1 \)
  5. \( x > 1 \)
Pembahasan »

Dengan menggunakan beberapa sifat bilangan berpangkat dan melakkan manipulasi aljabar, bentuk penjabaran pertidaksamaan yang diberikan kurang lebih sebagai berikut:

\begin{aligned} -2^{2x+1}+4^x+8^{x+\frac{1}{3}}-8^{\frac{2x-1}{3}}-16^{ \frac{2x-1}{4} } &> 0 \\[8pt] -1 \cdot 2^{2x} \cdot 2 + 2^{2x}+2^{3 \left( x + \frac{1}{3} \right)}-2^{3 \left( \frac{2x-1}{3} \right)}-2^{4 \left( \frac{2x-1}{4} \right)} &> 0 \\[8pt] -2 \cdot 2^{2x} + 2^{2x} + 2^{3x+1}-2^{2x-1}-2^{2x-1} &> 0 \\[8pt] -1 \cdot 2^{2x} + 2^{3x} \cdot 2 - 2 \cdot 2^{2x-1} &> 0 \\[8pt] -2^{2x}+2^{3x} \cdot 2 - 2^{2x-1+1} &> 0 \\[8pt] -2^{2x}+2^{3x} \cdot 2 - 2^{2x} &> 0 \\[8pt] -2 \cdot 2^{2x} + 2^{3x} \cdot 2 &> 0 \\[8pt] 2^{3x} \cdot 2 &> 2 \cdot 2^{2x} \\[8pt] 3x &> 2x \\[8pt] 3x-2x &> 0 \\[8pt] x &> 0 \end{aligned}

Jawaban B.

Contoh 6: SBMPTN 2019

Himpunan penyelesaian \( \left( \frac{1}{8} \right)^{8+2x-x^2} \geq \left( \frac{1}{16} \right)^{x+2} \) adalah…

  1. \( \left\{ x | x \leq -3 \ \text{atau} \ x \geq 2 \right\} \)
  2. \( \left\{ x | x \leq -3 \ \text{atau} \ x \geq \frac{3}{8} \right\} \)
  3. \( \left\{ x | x \leq -2 \ \text{atau} \ x \geq \frac{8}{3} \right\} \)
  4. \( \left\{ x | x \leq \frac{3}{8} \ \text{atau} \ x \geq \frac{8}{3} \right\} \)
  5. \( \left\{ x | x \leq 2 \ \text{atau} \ x \geq \frac{8}{3} \right\} \)
Pembahasan »

Salah satu sifat pertidaksamaan eksponen yaitu untuk \( a^{f(x)} > a^{g(x)} \) di mana \( 0 < a < 1 \) maka \( f(x) < g(x) \) (tanda pertidaksamaan berubah) sehingga dengan menggunakan sifat pertidaksamaan dan manipulasi aljabar, diperoleh:

\begin{aligned} \left( \frac{1}{8} \right)^{8+2x-x^2} &\geq \left( \frac{1}{16} \right)^{x+2} \\[8pt] \left( \frac{1}{2} \right)^{3(8+2x-x^2)} &\geq \left( \frac{1}{2} \right)^{4(x+2)} \\[8pt] \left( \frac{1}{2} \right)^{24+6x-3x^2} &\geq \left( \frac{1}{2} \right)^{4x+8} \\[8pt] 24+6x-3x^2 &\leq 4x+8 \\[8pt] 24+6x-3x^2-4x-8 &\leq 0 \\[8pt] -3x^2+2x+16 &\leq 0 \\[8pt] 3x^2-2x-16 &\geq 0 \\[8pt] (3x-8)(x+2) &\geq 0 \\[8pt] x = \frac{8}{3} \ \text{atau} \ x &= -2 \end{aligned}

Dari hasil di atas, diperoleh himpunan penyelesaian pertidaksamaan kuadrat yaitu \( x \leq -2 \) atau \( x \geq \frac{8}{3} \).

Jawaban C.

Contoh 7: SBMPTN 2019

Himpunan penyelesaian \( (0,25)^{x+2} > (0,5)^{x^2+1} \) adalah…

  1. \( -1 < x < 3 \)
  2. \( -1 < x < 0 \)
  3. \( 0 < x < 3 \)
  4. \( x < -1 \) atau \( x > 3 \)
  5. \( x < -2 \) atau \( x > 4 \)
Pembahasan »

Salah satu sifat pertidaksamaan eksponen yaitu untuk \( a^{f(x)} > a^{g(x)} \) di mana \( 0 < a < 1 \) maka \( f(x) < g(x) \) (tanda pertidaksamaan berubah) sehingga dengan menggunakan sifat pertidaksamaan dan manipulasi aljabar, diperoleh:

\begin{aligned} (0,25)^{x+2} &> (0,5)^{x^2+1} \\[8pt] (0,5)^{2x+4} &> (0,5)^{x^2+1} \\[8pt] 2x+4 &< x^2+1 \\[8pt] 2x+4-x^2-1 &< 0 \\[8pt] -x^2+2x+3 &< 0 \\[8pt] x^2-2x-3 &> 0 \\[8pt] (x+1)(x-3) &> 0 \\[8pt] x < -1 \ \text{atau} \ x &> 3 \end{aligned}

Jadi, himpunan penyelesaian pertidaksamaan \( (0,25)^{x+2} > (0,5)^{x^2+1} \) adalah \( x < -1 \) atau \( x > 3 \).

Jawaban D.

Contoh 8:

Jika pertidaksamaan \( \sqrt{3-ax} \leq 2 \) dipenuhi oleh interval \( a-2 \leq x \leq 3 \) maka nilai \( a^2-a = \cdots \)

  1. \( 4 \)
  2. \( 3 \)
  3. \( 2 \)
  4. \( 1 \)
  5. \( 0 \)
Pembahasan »

Kuadratkan kedua ruas pertidaksamaan \( \sqrt{3-ax} \leq 2 \) sehingga diperoleh \( 3-ax \leq 4 \). Dari syarat akar diperoleh \( 3-ax \geq 0 \). Dari sini, kita peroleh:

\begin{array}{rcccl} 0 & \leq & 3-ax & \leq & 4 \\[8pt] -3 & \leq & -ax & \leq & 1 \\[8pt] -\frac{1}{a} & \leq & x & \leq & \frac{3}{a} \end{array}

Karena diketahui bahwa pertidaksamaan \( \sqrt{3-ax} \leq 2 \) terpenuhi oleh interval \( a-2 \leq x \leq 3 \), maka jelas bahwa \(a = 1\).

Dengan demikian, nilai dari \( a^2-a=1^2-1 = 0 \).

Jawaban E.

Contoh 9:

Penyelesaian pertidaksamaan \( \sqrt{2x+6} > 0 \) adalah…

  1. \( x < 3 \)
  2. \( x \leq -3 \)
  3. \( x \geq -3 \)
  4. \( x > -3 \)
  5. \( x > 6 \)
Pembahasan »

Langkah pertama, kuadratkan ruas kiri dan kanan pertidaksamaannya, sehingga diperoleh:

\begin{aligned} \sqrt{2x+6} &> 0 \\[8pt] \left( \sqrt{2x+6} \right)^2 &> (0)^2 \\[8pt] 2x+6 &> 0 \\[8pt] 2x &> -6 \\[8pt] x &> -3 \end{aligned}

Dari hasil di atas diperoleh himpunan penyelesaiannya yaitu \( x > -3 \).

Langkah kedua, carilah nilai \(x\) yang memenuhi syarat akar \( \sqrt{2x+6} \). Ingat bahwa syarat akar yaitu \( 2x+6 \geq 0 \) sehingga diperoleh \( x \geq -3 \).

Irisan dari kedua langkah penyelesaian di atas merupakan himpunan penyelesaian dari pertidaksamaan akar yang diberikan dalam soal. Karena semua \(x\) yang memenuhi \(x > -3\) juga memenuhi syarat akar \( x \geq -3 \) maka penyelesaian pertidaksamaan \( \sqrt{2x+6} > 0 \) adalah \(x > -3\).

Jawaban D.

Contoh 10:

Jika \( \sqrt{3x-1} < 2 \) maka nilai \(x\) yang memenuhi pertidaksamaan tersebut adalah…

  1. \( x < \frac{5}{3} \)
  2. \( x > \frac{1}{3} \)
  3. \( \frac{1}{3} \leq x < \frac{5}{3} \)
  4. \( \frac{1}{3} < x < \frac{5}{3} \)
  5. \( \frac{1}{3} < x \leq \frac{5}{3} \)
Pembahasan »

Langkah pertama, selesaikan pertidaksamaan dengan mengkuadratkan kedua ruas persamaannya, diperoleh:

\begin{aligned} \sqrt{3x-1} &< 2 \\[8pt] \left( \sqrt{3x-1} \right)^2 &< (2)^2 \\[8pt] 3x-1 &< 4 \\[8pt] 3x &< 5 \\[8pt] x &< \frac{5}{3} \end{aligned}

Dari hasil di atas diperoleh himpunan penyelesaian pertidaksamaannya yaitu \(x < \frac{5}{3}\).

Langkah kedua, tentukan nilai \(x\) yang memenuhi syarat akar \( \sqrt{3x-1} \). Syarat akarnya yaitu \( 3x-1 \geq 0 \) sehingga diperoleh \( x \geq \frac{1}{3} \).

Irisan dari kedua langkah penyelesaian di atas merupakan himpunan penyelesaian pertidaksamaan akar yang diberikan dalam soal ini. Jika dilukiskan dalam garis bilangan kurang lebih seperti pada gambar berikut.

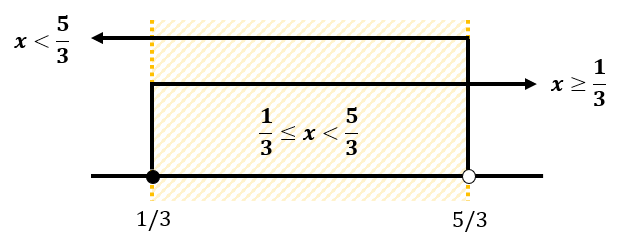
pertidaksamaan pecahan

Dari garis bilangan di atas tampak bahwa himpunan penyelesaian pertidaksamaan akar \( \sqrt{3x-1} < 2 \) adalah \( \frac{1}{3} \leq x < \frac{5}{3} \).

Jawaban C.

Contoh 11:

Semua bilangan real \(x\) yang memenuhi pertidaksamaan \( \sqrt{x^2+4x-5} < 4 \) adalah…

  1. \( -7 < x < -5 \) atau \( 1 < x \leq 3 \)
  2. \( -7 < x < -5 \) atau \( 1 \leq x \leq 3 \)
  3. \( -7 < x \leq -5 \) atau \( 1 \leq x < 3\)
  4. \( x < -7 \) atau \(x > 3\)
  5. \(x < 5\) atau \(x > 3\)
Pembahasan »

Langkah pertama, kuadratkan kedua ruas pertidaksamaannya sehingga diperoleh:

\begin{aligned} (\sqrt{x^2+4x-5})^2 &< 4^2 \\[8pt] x^2+4x-5 &< 16 \\[8pt] x^2+4x-21 &< 0 \\[8pt] (x+7)(x-3) &< 0 \\[8pt] HP: \ \{ x|-7 < x &< 3 \} \end{aligned}

Langkah kedua, tentukan nilai \(x\) agar bentuk akar terdefinisi atau mempunyai nilai real. Agar \( \sqrt{x^2+4x-5} \) mempunyai nilai real, maka syaratnya yaitu:

\begin{aligned} x^2+4x-5 &\geq 0 \\[8pt] (x+5)(x-1) &\geq 0 \\[8pt] \text{Pembuat nol:} \ x = -5 \ &\text{atau} \ x = 1 \\[8pt] HP: \{ x | x \leq -5 \ &\text{atau} \ x \geq 1 \} \end{aligned}

Dari kedua tahapan penyelesaian di atas, irisan dari nilai \(x\) yang diperoleh adalah himpunan penyelesaian pertidaksamaan akar yang diberikan dalam soal. Jika digambarkan hasilnya kurang lebih seperti berikut:

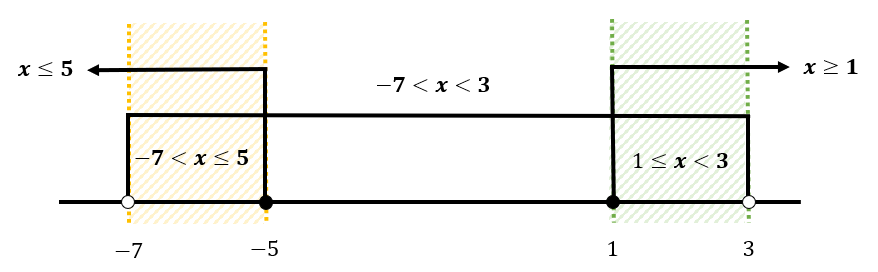
pertidaksamaan pecahan

Dari hasil di atas, himpunan penyelesaiannya adalah \( -7 < x \leq -5 \) atau \( 1 \leq x < 3 \).

Jawaban C.

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.

Artikel terkait