www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Limit Fungsi › Definisi Limit dan Limit Fungsi Aljabar
Definisi Limit dan Limit Fungsi Aljabar
Apa itu limit? Mungkin itulah pertanyaan pertama yang timbul ketika Anda mendengar istilah ini. Jika Anda mencari arti kata limit dalam Kamus Besar Bahasa Indonesia (KBBI), Anda akan menemukan bahwa limit itu artinya "batas".
Dalam matematika, limit bisa berarti pendekatan dan berhubungan dengan batas. Definisi dari limit menyatakan bahwa suatu fungsi \(f(x)\) akan mendekati suatu nilai tertentu jika \(x\) mendekati nilai tertentu.
Agar lebih jelas, pandang fungsi yang ditentukan oleh rumus

Perhatikan bahwa fungsi tersebut tidak terdefinisikan pada \(x =1\) karena di titik ini \(f(x)\) berbentuk \(0/0\), yang mana tidak mempunyai arti. Namun, kita masih dapat menanyakan apa yang terjadi pada \(f(x)\) bilamana \(x\) mendekati 1 atau lebih tepatnya, apakah \(f(x)\) mendekati bilangan tertentu bilamana \(x\) mendekati 1? Untuk sampai pada pertanyaan ini, kita telah melakukan tiga hal.
Pertama, kita telah menghitung beberapa nilai \(f(x)\) untuk \(x\) dekat 1. Kedua, kita menunjukkan nilai-nilai ini dalam sebuah diagram skematis (schematic diagram), dan terakhir kita telah mensketsakan grafik \(y = f(x)\) (Gambar 1).

Gambar 1. Tabel nilai, diagram skematis, dan grafik \(y = f(x)\)
Semua informasi yang telah kita sajikan di atas kelihatannya menunjuk ke kesimpulan yang sama yakni \(f(x)\) mendekati 3 jika \(x\) mendekati 1. Dalam lambang matematis, kita tuliskan

Ini dibaca “limit dari \((x^3 - 1)/(x - 1)\) untuk \(x\) mendekati 1 adalah 3.”
Sekarang Anda mungkin sudah lebih paham mengenai limit. Namun, kita tidak akan mencari nilai limit dari suatu fungsi dengan cara seperti yang dilakukan di atas. Selain memakan waktu, cara demikian juga sangat sulit untuk dikerjakan. Oleh karena itu, di sini kita akan belajar cara mencari nilai limit dengan metode-metode serta teorema-teorema yang telah ada.
Limit Fungsi Aljabar
Terdapat tiga metode untuk mengerjakan limit fungsi aljabar, yakni metode substitusi, metode pemfaktoran, dan metode perkalian dengan akar sekawan. Kita akan membahas satu per satu metode persebut.
Metode Substitusi
Metode substitusi merupakan yang paling mudah karena untuk menentukan hasil limit kita hanya perlu mensubstitusi atau memasukkan secara langsung nilai ke dalam fungsi pada limit. Sebagai contoh, perhatikan pengerjaan limit berikut
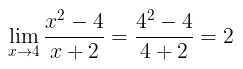
Meskipun mudah, kita tidak dapat selalu menggunakan metode ini terutama jika hasil substitusi memberikan nilai "tak tentu" seperti: \( \frac{∞}{∞}, \ \frac{0}{0}, \ 0⋅∞, \ ∞-∞, \ 0^0, \ ∞^0, \quad \text{atau} \quad ∞^∞ \)
Sebagai contoh, kita tidak bisa mengerjakan limit berikut dengan cara substitusi karena akan menghasilkan bentuk tak tentu 0/0, yakni

Oleh karena itu, kita memerlukan metode lain untuk mengerjakan limit yang demikian. Kita akan melihat bahwa limit yang demikian dapat diselesaikan dengan metode pemfaktoran.
Metode Pemfaktoran
Perhatikan kembali limit yang tak dapat dikerjakan dengan cara substitusi di atas. Untuk menyelesaikan limit tersebut, kita perlu memfaktorkan fungsinya terlebih dahulu, baru kemudian kita mensubstitusikan nilainya. Perhatikan berikut ini.

Meskipun metode pemfaktoran dapat menangani masalah limit yang tak dapat dikerjakan dengan cara substitusi di atas, bukan berarti ini berlaku untuk setiap kasus. Sayangnya, dalam beberapa kasus, metode pemfaktoran tidak dapat membantu begitu pula dengan metode substitusi. Perhatikan limit berikut ini.
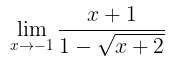
Baik metode substitusi maupun metode pemfaktoran tidak dapat diterapkan untuk menemukan nilai limit tersebut. Jika kita menggunakan substitusi langsung, maka kita akan peroleh bentuk tak tentu 0/0 yang mana tidak memberikan arti apapun.
Begitu pula, kita tidak dapat memfaktorkan fungsi pada limit tersebut sehingga metode pemfaktoran juga tak dapat diterapkan. Untuk menangani limit yang demikian, kita perlu mengenal metode berikutnya yakni metode perkalian dengan akar sekawan.
Metode Perkalian dengan Akar Sekawan
Inti dari metode ini yaitu mengalikan fungsi pada limit dengan akar sekawannya. Kita akan menggunakan contoh limit di atas yang tak dapat dikerjakan dengan metode substitusi langsung dan juga metode pemfaktoran. Perhatikan berikut.
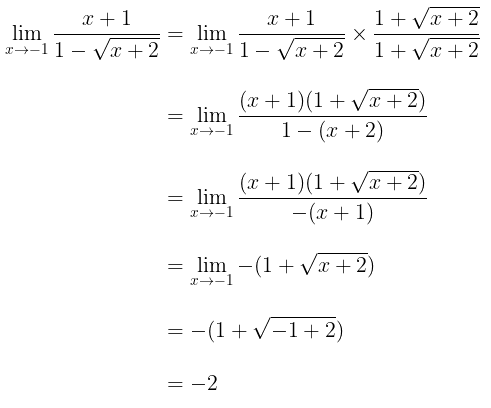
Perhatikan pengerjaan limit di atas. Pertama kita melakukan perkalian dengan akar sekawan, kemudian melakukan pemfaktoran dan terakhir mensubstitusi langsung nilai pada fungsi hasil pemfaktoran sehingga diperoleh nilai limit yakni -2.
Teorema-teorema untuk Limit Fungsi Aljabar
Berikut ini sejumlah teorema yang bermanfaat untuk mengerjakan limit fungsi aljabar.

Contoh-contoh
Berikut ini akan diberikan sejumlah contoh soal terkait limit dan pengerjaannya dengan ketiga metode yang telah dijelaskan serta dengan menggunakan teorema-teorema limit di atas.
Contoh 1:
Tentukan nilai dari

Pembahasan:
Untuk mengerjakan soal ini, lakukan pemfaktoran untuk menyederhanakan fungsi dalam limit. Kemudian substitusikan nilai \(x\) untuk memperoleh nilai limit.

Contoh 2:
Tentukanlah nilai dari

Pembahasan:
Untuk mengerjakan soal ini, kita lakukan operasi aljabar untuk menyederhanakan fungsi dalam limit terlebih dahulu. Kemudian substitusikan nilai \(x\) untuk memperoleh nilai limit.

Contoh 3:
Hitunglah nilai dari

Pembahasan:
Untuk mengerjakan soal ini, kita gunakan metode perkalian dengan akar sekawan seperti yang sudah dijelaskan di atas, yakni

Contoh 4:
Hitunglah nilai dari
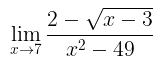
Pembahasan:
Kita gunakan metode perkalian dengan akar sekawan seperti yang sudah dijelaskan di atas, yakni

Contoh 5:
Tentukan nilai dari

Pembahasan:
Kita lakukan pemfaktoran terlebih dahulu untuk menyederhanakan fungsi dalam limit, kemudian substitusi nilai \(x\) untuk memperoleh nilai limit.

Contoh 6:
Tentukan nilai dari

Pembahasan:
Kita gunakan metode perkalian dengan akar sekawan seperti yang sudah dijelaskan di atas, yakni

Contoh 7:
Tentukan nilai dari
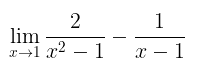
Pembahasan:
Kita sederhanakan fungsi dalam limit terlebih dahulu, kemudian substitusi nilai \(x\) untuk memperoleh nilai limit, yakni

Contoh 8:
Jika diketahui

Berapakah nilai \(a-b\)?
Pembahasan:

Persamaan kuadrat pembilang adalah

Dengan demikian, \( a = -20 \) dan \( b = -44 \) sehingga

Contoh 9:
Tentukan nilai dari
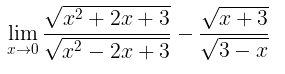
Pembahasan:
Kita gunakan metode perkalian dengan akar sekawan seperti yang sudah dijelaskan di atas, yakni

Sumber:
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Don't limit your challenges - challenge your limits.
