
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Bahas Soal Matematika » Matriks › 30 Contoh Soal dan Pembahasan Matriks Matematika SMA
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552
30 Contoh Soal dan Pembahasan Matriks Matematika SMA
Salah satu materi matematika yang biasanya disenangi oleh sebagian besar siswa adalah matriks. Ini karena materi matriks mudah untuk dipahami dan hanya memerlukan sedikit ketelitian dan kesabaran.
Kita telah mempelajari materi matriks secara panjang lebar pada beberapa artikel sebelumnya. Di artikel kita akan memperdalam pemahaman mengenai matriks dengan mengerjakan soal-soal matriks yang sering keluar baik saat ujian sekolah maupun ujian masuk perguruan tinggi.
Sebelum masuk ke contoh soal dan pembahasan, beberapa konsep matriks berikut sebaiknya sudah Anda kuasai terlebih dahulu:
- Operasi matriks
- Determinan matriks
- Invers matriks
Untuk lebih jelasnya, kita langsung masuk ke contoh soal dan pembahasan mengenai matriks berikut ini.
Contoh 1:
Berikut ini adalah persamaan matriks:
\begin{aligned} \begin{bmatrix} 4 & -2 \\ -6 & 8 \end{bmatrix} \begin{bmatrix} -1 & 1 \\ x & x-y \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \end{aligned}
Nilai \(x + y = \cdots \)
- 7/2
- -5
- -7/3
- 7/5
- -7/2
Dari soal diketahui bahwa

Dari hasil di atas diperoleh hubungan:

Dengan demikian,

Jawaban E.
Contoh 2:
Jika matriks \( A = \begin{bmatrix} 2 & 1 \\ x & 3 \end{bmatrix}, \ B = \begin{bmatrix} x & 2 \\ -4 & -y \end{bmatrix} \) dan \( C = \begin{bmatrix} 8 & 0 \\ 6 & -4 \end{bmatrix} \) dengan \(2A-B=C\), maka nilai \(x-y=\cdots\)
- -1
- 4
- -3
- 6
- 5
Dari soal, matriks A, B, dan C telah diberikan, sehingga:

Dari hasil di atas, kita peroleh hubungan berikut:

Jawaban D.
Contoh 3:
Terdapat dua buah matriks P dan Q yaitu \( P = \begin{bmatrix} 4 & a \\ 0 & 3 \end{bmatrix} \) dan \( Q = \begin{bmatrix} 10 & b \\ 0 & 6 \end{bmatrix} \). Jika \( PQ = QP \), maka \( \frac{a}{b} = \cdots \)
- 1/2
- 1/3
- 1/4
- 2/3
- 3/4
Dari soal diketahui \( PQ = QP \) sehingga:

Dari hasil di atas diperoleh hubungan berikut:
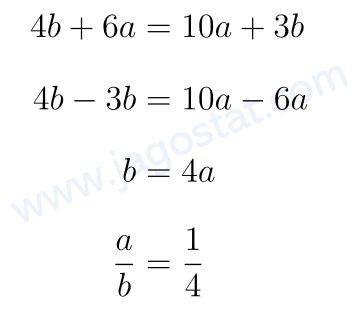
Jawaban C.
Contoh 4:
Jika \( \begin{bmatrix} {}^x \! \log a & \log 3a + 1 \\ \log (b-7) & 2 \end{bmatrix} = \begin{bmatrix} \log b & 1 \\ \log a & 1 \end{bmatrix} \). Nilai \( x = \cdots \)
- 1
- 2
- 3
- 4
- 5
Dari persamaan matriks di atas, kita peroleh hubungan berikut:
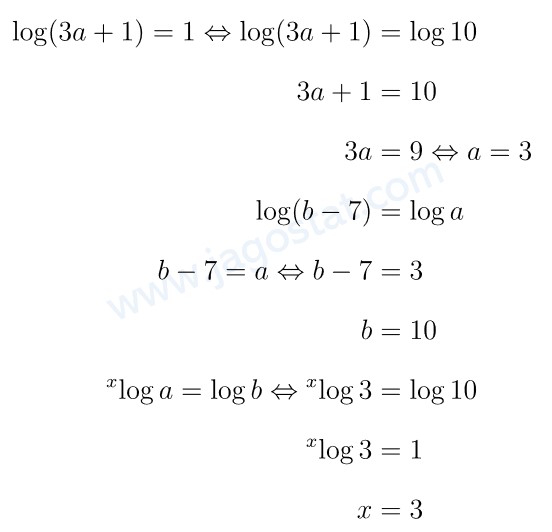
Jawaban C.
Contoh 5: UM UGM 2004
Jika \(I\) adalah matriks satuan dan matriks \( A = \begin{bmatrix} 2 & 1 \\ -4 & 3 \end{bmatrix} \) sehingga \( A^2 = pA + qI \), maka \( p + q \) sama dengan…
- 15
- 10
- 5
- -5
- -10
Dari soal diketahui \( A^2 = pA + qI \) sehingga:

Dari hasil di atas diperoleh,

Jawaban D.
Contoh 6: SNMPTN 2009 DASAR
Matriks \( A = \begin{bmatrix} 3 & 2 \\ 4 & 1 \end{bmatrix} \) mempunyai hubungan dengan matriks \( B = \begin{bmatrix} 1 & -4 \\ -2 & 3 \end{bmatrix} \). Jika matriks \( C = \begin{bmatrix} 5 & -3 \\ -3 & 2 \end{bmatrix} \) dan matriks D mempunyai hubungan serupa seperti A dengan B maka matriks \( C + D \) adalah…
- \( \begin{bmatrix} 2 & 3 \\ 3 & 5 \end{bmatrix} \)
- \( \begin{bmatrix} 0 & 7 \\ 7 & 0 \end{bmatrix} \)
- \( \begin{bmatrix} 0 & -7 \\ -7 & 0 \end{bmatrix} \)
- \( \begin{bmatrix} 7 & 0 \\ 0 & 7 \end{bmatrix} \)
- \( \begin{bmatrix} 7 & 7 \\ 0 & 0 \end{bmatrix} \)
Matriks \( A = \begin{bmatrix} 3 & 2 \\ 4 & 1 \end{bmatrix} \) dan \( B = \begin{bmatrix} 1 & -4 \\ -2 & 3 \end{bmatrix} \) memiliki hubungan yaitu elemen diagonal utama ditukar tempat dan elemen selain diagonal utama juga ditukar tetapi diberikan tanda negatif (-). Jadi, jika \( C = \begin{bmatrix} 5 & -3 \\ -3 & 2 \end{bmatrix} \) dan D juga mempunyai hubungan serupa seperti A dengan B, maka \( D = \begin{bmatrix} 2 & 3 \\ 3 & 5 \end{bmatrix}\). Dengan demikian,
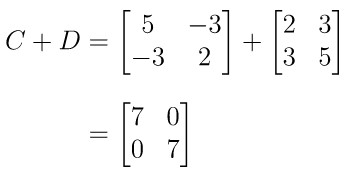
Jawaban D.
Contoh 7: (SNMPTN 2014 DASAR)
Jika \( \begin{bmatrix} a & b \\ b & 2a \end{bmatrix} \begin{bmatrix} x \\ x + y \end{bmatrix} = \begin{bmatrix} a \\ b \end{bmatrix} \) dengan \( b^2 \neq 2a^2 \) maka \( x + y = \cdots \)
- -2
- -1
- 0
- 1
- 2
Misalkan \( A = \begin{bmatrix} a & b \\ b & 2a \end{bmatrix} \) dan \( B = \begin{bmatrix} a \\ b \end{bmatrix} \) sehingga:

Selanjutnya, \(x+y\) dapat dicari dengan determinasi, yaitu:

Jawaban C.
Contoh 8: (EBTANAS 2000)
Diketahui \( A = \begin{bmatrix} 2 & 3 \\ -1 & -2 \end{bmatrix} \) dan \(B = \begin{bmatrix} 6 & 12 \\ -4 & -10 \end{bmatrix} \) dan \( A^2 = xA + yB \). Nilai \(xy = \cdots \)
- -4
- -1
- \( -\frac{1}{2} \)
- \(1 \frac{1}{2}\)
- 2
Dari soal diketahui \( A^2 = xA + yB \) sehingga:

Dari persamaan di atas kita peroleh

Dengan menyelesaikan persamaan (1) dan (2), kita peroleh nilai \( y = -\frac{1}{2}\) dan \( x = 2\). Jadi, nilai \( xy = -\frac{1}{2} \cdot 2 = -1 \).
Jawaban B.
Contoh 9: SBMPTN 2014 DASAR
Jika matriks \( A = \begin{bmatrix} 2x & -2 \\ x & 3y+2 \end{bmatrix}, \ B = \begin{bmatrix} 9 & 3x \\ 8 & -4 \end{bmatrix} \) dan \( C = \begin{bmatrix} 5 & 6 \\ -8 & 7 \end{bmatrix} \) memenuhi \( A + B = C^t \) dengan \(C^t\) transpos matriks \(C\), maka \(2x+3y = \cdots\)
- 3
- 4
- 5
- 6
- 7
Dari soal diketahui bahwa \( A + B = C^t \) sehingga kita peroleh berikut:

Dari hasil di atas diperoleh \( 2x + 9 = 5 \) sehingga \(x = -4\) dan \( 3y-2 = 7 \) sehingga \( 3y = 9 \). Dengan demikian, \( 2x + 3y = -4 + 9 = 5 \)
Jawaban C.
Contoh 10:
Jika matriks \( A = \begin{bmatrix} \ 1 & -2 \ \\[8pt] \ 0 & \ \ 1 \ \end{bmatrix}\), maka \(A^{25} \begin{bmatrix} \ 25 \ \\[8pt] \ 1 \ \end{bmatrix} = \cdots \)
- \( \begin{bmatrix} -25 \\[8pt] 1 \end{bmatrix} \)
- \( \begin{bmatrix} 25 \\[8pt] 1 \end{bmatrix} \)
- \( \begin{bmatrix} -25 \\[8pt] -1 \end{bmatrix} \)
- \( \begin{bmatrix} 1 \\[8pt] 25 \end{bmatrix} \)
- \( \begin{bmatrix} 1 \\[8pt] -25 \end{bmatrix} \)
Untuk menyelesaikan soal ini, kita perlu mencari matriks dari \(A^{25}\) terlebih dahulu. Untuk cara cepatnya yaitu kita hitung dulu matriks \(A\) ketika dipangkatkan dengan angka yang kecil misalnya 2, 3, dan 4. Kemudian dari hasil yang diperoleh kita cari polanya. Setelah polanya ketemu kita dapat mencari matriks \(A^{25}\) dengan mudah.
Kita langsung aja hitung matriks \(A\) pangkat 2 dan \(A\) pangkat 3 sebagai berikut:

Dari hasil di atas, kita peroleh:

Jika persamaan umum untuk matriks \(A, \ A^2\), dan \(A^3\) di atas adalah \( \begin{bmatrix} \ a_{11} & a_{12} \ \\[8pt] \ a_{21} & \ a_{22} \ \end{bmatrix} \), maka kita peroleh pola untuk matriks \(A^n = \begin{bmatrix} \ a_{11} & U_n \ \\[8pt] \ a_{21} & \ a_{22} \ \end{bmatrix} \) di mana \(U_n\) adalah barisan aritmatika dengan suku pertama (a) dan bedanya (b) adalah -2. Kita peroleh \(U_n\), yaitu:

Jadi, matriks \(A^{25}\) yaitu:

Dengan demikian,
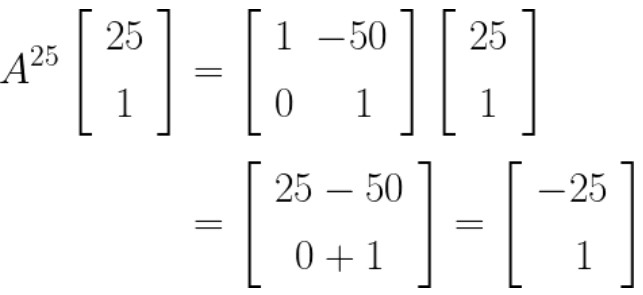
Jawaban A.
Contoh 11:
Jika matriks \( A = \begin{bmatrix} 2 & -3 \\ 3 & -5 \end{bmatrix}, \ B = \begin{bmatrix} -1 & 4 \\ -3 & 2 \end{bmatrix} \), dan \( C = \begin{bmatrix} 6 & 8 \\ 10 & 16 \end{bmatrix} \), maka nilai determinan dari matriks \( (AB + C) = \cdots \)
- 10
- 14
- 18
- 24
- 50
Kita cari dulu matriks dari \( AB + C \), yakni:

Determinan dari matriks \( (AB+C) \), yaitu:

Jawaban B.
Contoh 12: (EBTANAS 2003)
Nilai \( x^2 + 2xy + y^2 \) yang memenuhi persamaan \( \begin{bmatrix} 2 & 6 \\ 1 & -3 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 2 \\ -5 \end{bmatrix} \)
- 1
- 3
- 5
- 7
- 9
Kita bisa mencari nilai \( x \) dan \( y \) menggunakan aturan cramer.

Dengan demikian,

Jawaban A.
Contoh 13: UTBK-SBMPTN 2019
Diketahui matriks \( A = \begin{pmatrix} 2 & 1 \\ 3 & 5 \end{pmatrix} \) mempunyai hubungan dengan matriks \( B = \begin{pmatrix} -5 & 3 \\ 1 & -2 \end{pmatrix} \). Matriks \(C = \begin{pmatrix} 3 & 2 \\ 1 & -5 \end{pmatrix} \) dan matriks D mempunyai hubungan yang serupa dengan A dan B. Bentuk \( C + D = \cdots \)
- \( \begin{pmatrix} 8 & 3 \\ 3 & -8 \end{pmatrix} \)
- \( \begin{pmatrix} 8 & 3 \\ 3 & -2 \end{pmatrix} \)
- \( \begin{pmatrix} 5 & 1 \\ 2 & -3 \end{pmatrix} \)
- \( \begin{pmatrix} 3 & -2 \\ -1 & -5 \end{pmatrix} \)
- \( \begin{pmatrix} -3 & 2 \\ 1 & 5 \end{pmatrix} \)
Hubungan matriks A dan B, yaitu:
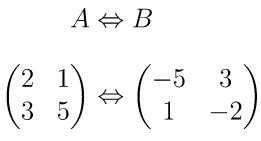
Jika kita perhatikan bahwa kedua matriks tersebut elemen-elemen pada diagonal utamanya bertukar tempat lalu dikalikan dengan -1 dan elemen-elemen pada diagonal selain diagonal utama juga bertukar tempat. Berdasarkan hubungan antara matriks A dan B, maka matriks D yaitu:

Dengan demikian,

Jawaban A.
Contoh 14: UNBK Matematika IPS 2019
Diketahui matriks \( A = \begin{pmatrix} 4x-y & -2 \\ z & 4 \end{pmatrix} \), \( B = \begin{pmatrix} 2 & y+2 \\ 1 & z-x \end{pmatrix} \) dan \( C = \begin{pmatrix} 4 & 8 \\ -10 & 10 \end{pmatrix} \) dan \( C^T \) adalah transpose matriks C. Jika \( 3A-B=C^T \), nilai dari \( -3x+y+5z \) adalah…
- 8
- 10
- 14
- 16
- 20

Jawaban C.
Contoh 15: SIMAK UI 2019
Diketahui \( A = \begin{pmatrix} 1 & 2 \\ 2 & 1 \end{pmatrix} \) dan \( B = \begin{pmatrix} -1 & 2 \\ 1 & 1 \end{pmatrix} \). Jika \( A + tB \) merupakan matriks singular, nilai \( t^2+3t+2 \) adalah…
- 0
- 1
- 2
- 3
- 5
Ingat bahwa matriks dikatakan singular jika determinannya sama dengan nol, sehingga kita peroleh:

Jawaban A.
Contoh 16: UM UGM 2004
Jika M matriks berordo 2x2 dan \( M \begin{pmatrix} 2 & 1 \\ 4 & 3 \end{pmatrix} = \begin{pmatrix} -2 & 1 \\ 14 & 10 \end{pmatrix} \), maka matriks \(M^2\) adalah…
- \( \begin{pmatrix} 3 & 2 \\ 1 & 5 \end{pmatrix} \)
- \( \begin{pmatrix} 9 & 4 \\ 1 & 25 \end{pmatrix} \)
- \( \begin{pmatrix} 27 & -4 \\ -2 & 11 \end{pmatrix} \)
- \( \begin{pmatrix} 25 & -4 \\ -2 & 15 \end{pmatrix} \)
- \( \begin{pmatrix} 27 & -8 \\ -4 & 15 \end{pmatrix} \)
Berdasarkan sifat perkalian matriks bahwa \( A \cdot B = C \) maka \( A = C \cdot B^{-1} \), kita peroleh berikut ini:
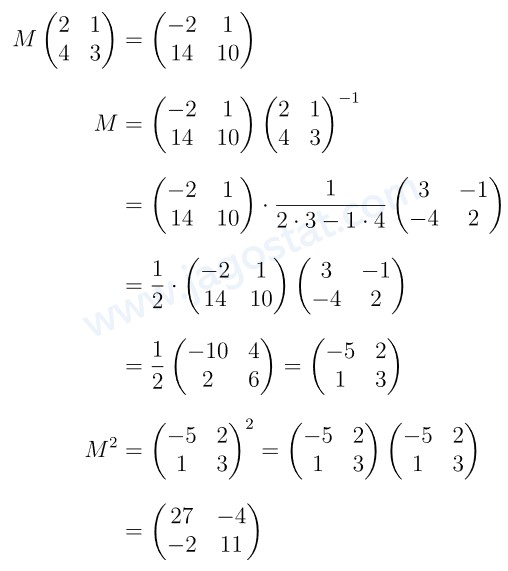
Jawaban C.
Contoh 17: UM UGM 2004
Hasil kali matriks \( A \begin{pmatrix} 5 & -3 \\ 0 & 6 \end{pmatrix} = \begin{pmatrix} -10 & 30 \\ 35 & -27 \end{pmatrix} \). Matriks A adalah…
- \( \begin{pmatrix} -1 & -1 \\ 4 & 7 \end{pmatrix} \)
- \( \begin{pmatrix} -2 & 4 \\ 7 & -1 \end{pmatrix} \)
- \( \begin{pmatrix} 4 & -2 \\ 7 & -1 \end{pmatrix} \)
- \( \begin{pmatrix} 7 & 2 \\ -1 & 4 \end{pmatrix} \)
- \( \begin{pmatrix} 7 & 2 \\ 4 & -1 \end{pmatrix} \)
Ingat bahwa untuk matriks \( A \cdot B = C \) maka \( A = C \cdot B^{-1} \) sehingga kita peroleh:

Jawaban B.
Contoh 18: SPMB 2007
Pada matriks \( A = \begin{pmatrix} 1 & a \\ b & c \end{pmatrix} \), jika bilangan positif \( 1, a, c \) membentuk barisan geometri berjumlah 13 dan bilangan positif \(1,b,c\) membentuk barisan aritmatika, maka \( \det A = \cdots \)
- 17
- 6
- -1
- -6
- -22
Untuk menyelesaikan soal di atas kita perlu memahami materi barisan aritmatika dan geometri.
Barisan geometri \( 1, a, c \) berjumlah 13 sehingga berlaku:

Dari barisan aritmatika \( 1,b,c \) berlaku:

Dengan demikian, determinan matriks A, yaitu:
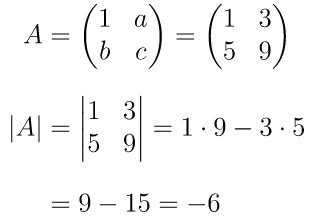
Jawaban D.
Contoh 19: SPMB 2006
Jika konstanta \(k\) memenuhi persamaan \( \begin{pmatrix} k & 1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} x-1 \\ y-1 \end{pmatrix} = \begin{pmatrix} 0 \\ k \end{pmatrix} \), maka \( x + y = \cdots \)
- \( (2+k)(1+k) \)
- \( (2-k)(1+k) \)
- \( (2-k)(1-k) \)
- \( (1+k)(1-k) \)
- \( (1-k)(2+k) \)
Ingat bahwa untuk \( A \cdot B = C \) maka \( B = A^{-1} \cdot C \), sehingga kita peroleh berikut:
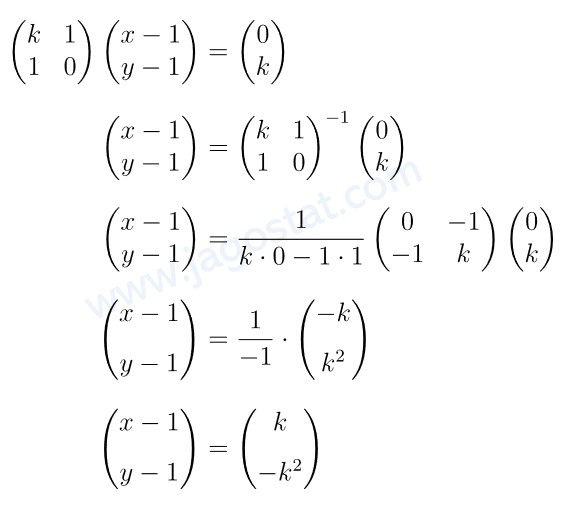
Dari kesamaan matriks di atas kita peroleh:

Jawaban B.
Contoh 20: UM UGM 2005
Jika \( \begin{pmatrix} x & y \end{pmatrix} \begin{pmatrix} \sin \alpha & \cos \alpha \\ -\cos \alpha & \sin \alpha \end{pmatrix} = (\sin \alpha \cos \alpha) \) dan \( \alpha \) suatu konstanta maka \( x+y = \cdots \)
- -2
- -1
- 0
- 1
- 2
Perhatikan bahwa elemen matriks mengandung fungsi trigonometri sehingga materi identitas trigonometri penting untuk dipahami terutama \( \sin^2 \alpha + \cos^2 \alpha = 1 \).

Dari kesamaan matriks di atas kita peroleh \( x = 1 \) dan \( y = 0 \) sehingga \( x+y = 1 \).
Jawaban D.
Contoh 21: SPMB 2005 Regional I
Jika \(x\) dan \(y\) memenuhi persamaan matriks \( \begin{pmatrix} p & q \\ q & p \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} p \\ q \end{pmatrix} \), \( p \neq q, p\neq 0 \) dan \( q \neq 0 \), maka \( x+y = \cdots \)
- -2
- -1
- 0
- 1
- 2
Ingat bahwa untuk \( A \cdot B = C \) maka \( B = A^{-1} \cdot C \) sehingga:

Dari kesamaan matriks di atas, kita peroleh \( x = 1 \) dan \( y = 0 \) sehingga \(x + y = 1\).
Jawaban D.
Contoh 22: SPMB 2005 Regional III
Jika \( \det \begin{pmatrix} x & -3 \\ 1 & 2x \end{pmatrix} = \det \begin{pmatrix} x & 1 \\ 3 & 8 \end{pmatrix} \), maka \( x = \cdots \)
- 1 atau 2
- 1 atau 3
- 2 atau 3
- -1 atau 2
- -2 atau 3
Berdasarkan rumus determinan matriks, kita dapatkan hasil berikut:

Jawaban B.
Contoh 23: UM UGM 2004
Bila \( A = \begin{pmatrix} \sin^2 x & -\cos x \\ \sqrt{3} \sin x & 1 \end{pmatrix} \) di mana \( 0 < x < \frac{\pi}{2} \) dan determinan A sama dengan 1, maka \(x\) adalah…
- 0
- \( \frac{\pi}{6} \)
- \( \frac{\pi}{4} \)
- \( \frac{\pi}{3} \)
- \( \frac{\pi}{2} \)
Elemen matriks A mengandung trigonometri sehingga untuk menyelesaikan soal ini perlu pemahaman rumus identitas trigonometri dan sudut istimewa trigonometri. Dari rumus identitas trigonometri, \( \sin^2 x + \cos^2 x = 1 \).
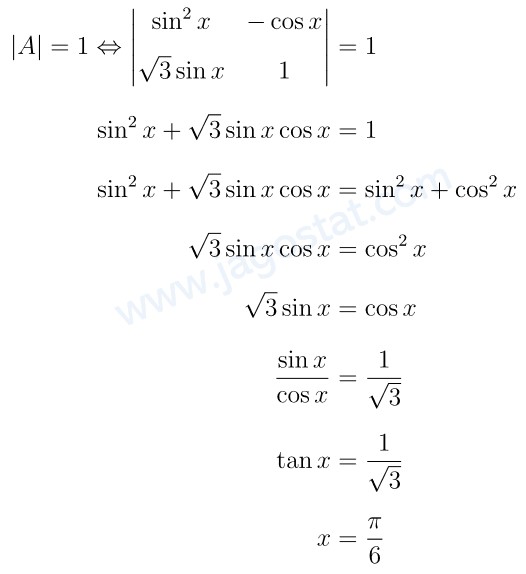
Jawaban B.
Contoh 24: SPMB 2004 Regional III
Transpos dari matriks P adalah \( P^T \). Jika matriks \( A = \begin{pmatrix} 3 & 7 \\ 1 & 2 \end{pmatrix}, B = \begin{pmatrix} 4 & 1 \end{pmatrix} \), dan \( C = \begin{pmatrix} x \\ y \end{pmatrix} \) memenuhi \( A^{-1} B^T = C \), maka \(x+y = \cdots\)
- -2
- -1
- 0
- 1
- 2
Dengan menggunakan aturan invers dan perkalian pada matriks, kita peroleh hasil berikut:

Dari kesamaan matriks di atas, kita peroleh \(x = -1\) dan \(y = 1\) sehingga \(x+y=0\).
Jawaban C.
Contoh 25: SPMB 2004 Regional III
Jika matriks \( A = \begin{pmatrix} 2 & 1 \\ -2 & 3 \end{pmatrix}, B = \begin{pmatrix} a \\ 1 \end{pmatrix} \), dan \( C = \begin{pmatrix} 11 \\ 1-4b \end{pmatrix} \) memenuhi \( AB = C \), maka \( |a-b| = \cdots \)
- 2
- 3
- 4
- 5
- 6
Dengan menggunakan aturan perkalian pada matriks, kita dapatkan hasil berikut:

Jawaban B.
Contoh 26: SNMPTN 2010
Jika \( M \) adalah matriks sehingga \( M \times \begin{pmatrix} a & b \\ c & d \end{pmatrix} = \begin{pmatrix} a+c & b+d \\ -c & -d \end{pmatrix} \), maka determinan matriks M adalah…
- -2
- -1
- 0
- 1
- 2
Dengan menggunakan sifat determinan matriks, kita peroleh berikut:
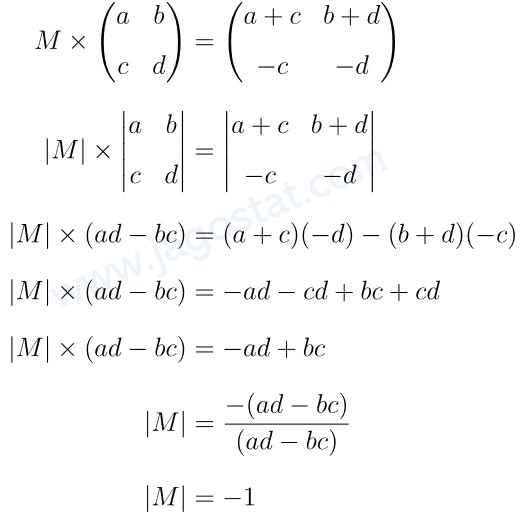
Jawaban B.
Contoh 27: SNMPTN 2010
Jika M adalah matriks sehingga \( M \times \begin{pmatrix} a & b \\ c & d \end{pmatrix} = \begin{pmatrix} a & b \\ a-c & b-d \end{pmatrix} \), maka determinan matriks M adalah
- -3
- -1
- 0
- 1
- 3
Dengan menggunakan sifat determinan matriks, kita peroleh berikut:

Jawaban B.
Contoh 28: SIMAK UI 2010
Diketahui \( AX = B \) dan \( BC = D \). Jika \( A = \begin{pmatrix} 1 & 2 \\ -3 & -5 \end{pmatrix}, C = \begin{pmatrix} 3 & 2 \\ 1 & 1 \end{pmatrix} \) dan \( D = \begin{pmatrix} 7 & 2 \\ 5 & 1 \end{pmatrix} \), maka \(X\) adalah…
- \( \begin{pmatrix} 2 & 1 \\ 41 & -19 \end{pmatrix} \)
- \( \begin{pmatrix} 33 & 54 \\ 19 & 31 \end{pmatrix} \)
- \( \begin{pmatrix} -33 & 19 \\ 54 & -31 \end{pmatrix} \)
- \( \begin{pmatrix} -33 & 54 \\ 19 & -31 \end{pmatrix} \)
- \( \begin{pmatrix} -41 & -2 \\ 19 & 1 \end{pmatrix} \)
Berdasarkan sifat matriks bahwa untuk \( A \cdot B = C \) maka \( A = C \cdot B^{-1} \), kita peroleh hasil berikut:

Jawaban D.
Contoh 29: UM UGM 2004
Jika \( \begin{pmatrix} -1 & 2 & 0 \\ 3 & -1 & 2 \end{pmatrix} \begin{pmatrix} -1 & 1 \\ 1 & 0 \\ 2 & 1 \end{pmatrix} + \begin{pmatrix} p & q \\ r & s \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \), maka \( p+q+r+s = \cdots \)
- -5
- -4
- 3
- 4
- 5

Dengan demikian,

Jawaban A.
Contoh 30: SBMPTN 2015 MATDAS
Jika \( A = \begin{pmatrix} 2 & 1 \\ a & 4 \end{pmatrix} \) merupakan matriks yang mempunyai invers dan \( \det B = 4 \) maka hasil kali semua nilai \(a\) yang mungkin sehingga \( \det A = 16 \cdot \det((AB)^{-1}) \) adalah…
- 6
- 10
- 20
- 30
- 60
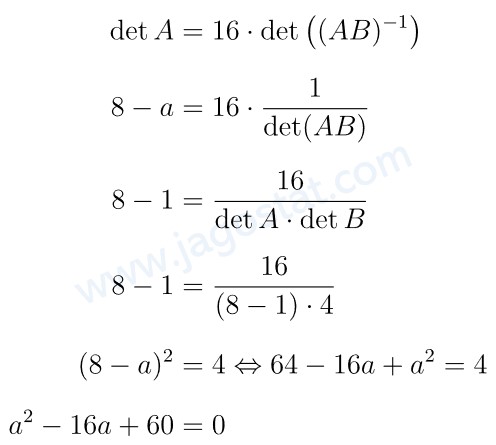
Ingat bahwa rumus perkalian akar-akar persamaan kuadrat yaitu \( x_1 \cdot x_2 = \frac{c}{a} \) sehingga hasil kali semua nilai \(a\) yang mungkin adalah \( a_1 \cdot a_2 = \frac{60}{1} = 60 \).
Jawaban E.
Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan jika ada yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima Kasih.
Oleh Tju Ji Long · Statistisi
Artikel Terkait
Anda hidup hanya sekali, tetapi jika Anda melakukannya dengan benar, sekali itu cukup.