www.jagostat.com

www.jagostat.com

Website Belajar Matematika & Statistika

Website Belajar Matematika & Statistika

Bahas Soal Matematika   »   Matriks   ›  Contoh Soal dan Pembahasan Invers Matriks Matematika SMA
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552

Contoh Soal dan Pembahasan Invers Matriks Matematika SMA

Artikel ini membahas berbagai contoh soal yang berkaitan dengan invers matriks. Misalkan terdapat dua matriks yakni matriks \(A\) dan matriks \(B\). Matriks \(A\) disebut invers dari matriks \(B\) jika berlaku \(AB=BA=I\), di mana \(I\) merupakan matriks identitas.

Invers dari matriks \(B\) ditulis dengan \( B^{-1} \) dan invers dari matriks \(A\) yaitu \( A^{-1} \).

Contoh 1: UNBK Matematika IPS 2018

Diketahui matriks \( A = \begin{pmatrix} 3 & 0 \\ 2 & 0 \end{pmatrix} \); \( B = \begin{pmatrix} 2 & 1 \\ 3 & 2 \end{pmatrix} \), dan \( A + B = C \). Invers matriks \(C\) adalah…

  1. \( \begin{pmatrix} \frac{2}{5} & -\frac{1}{5} \\ -1 & 1 \end{pmatrix} \)
  2. \( \begin{pmatrix} 1 & -\frac{1}{5} \\ -1 & \frac{2}{5} \end{pmatrix} \)
  3. \( \begin{pmatrix} 1 & \frac{1}{5} \\ -1 & \frac{2}{5} \end{pmatrix} \)
  4. \( \begin{pmatrix} \frac{2}{5} & \frac{1}{5} \\ 1 & \frac{2}{5} \end{pmatrix} \)
  5. \( \begin{pmatrix} \frac{2}{5} & -1 \\ \frac{1}{5} & 1 \end{pmatrix} \)
Pembahasan »

Berdasarkan informasi dalam soal, kita peroleh berikut:

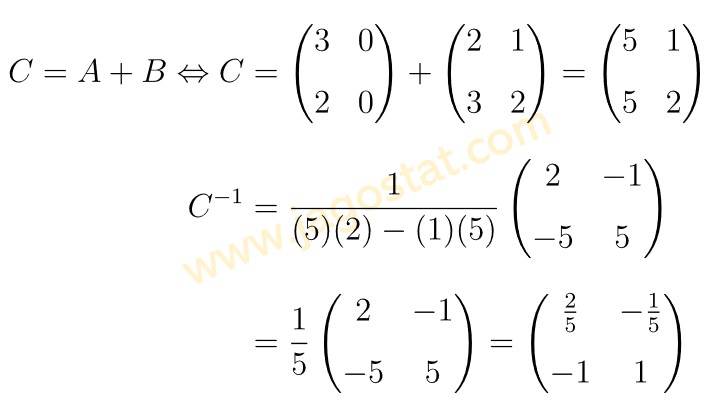
contoh soal invers matriks dan pembahasannya

Jawaban A.

Contoh 2: UNBK Matematika IPA 2018

Diketahui matriks \( A = \begin{pmatrix} 2 & 1 \\ 4 & -1 \end{pmatrix} \) dan \( B = \begin{pmatrix} 4 & -1 \\ 1 & 1 \end{pmatrix} \). Jika \( C = AB\), invers matriks \(C\) adalah….

  1. \( \begin{pmatrix} \frac{1}{6} & -\frac{1}{30} \\ \frac{1}{2} & -\frac{3}{10} \end{pmatrix} \)
  2. \( \begin{pmatrix} -\frac{1}{6} & \frac{1}{2} \\ -\frac{1}{30} & -\frac{3}{10} \end{pmatrix} \)
  3. \( \begin{pmatrix} \frac{1}{6} & -\frac{1}{2} \\ -\frac{1}{30} & -\frac{3}{10} \end{pmatrix} \)
  4. \( \begin{pmatrix} \frac{1}{6} & -\frac{1}{30} \\ -\frac{1}{2} & \frac{3}{10} \end{pmatrix} \)
  5. \( \begin{pmatrix} -\frac{1}{6} & -\frac{1}{2} \\ -\frac{1}{30} & -\frac{3}{10} \end{pmatrix} \)
Pembahasan »

Berdasarkan informasi yang diberikan dalam soal, kita peroleh hasil berikut:

contoh soal invers matriks dan pembahasannya

Jawaban A.

Contoh 3: SBMPTN 2014

Jika \( A = \begin{pmatrix} 2 & 3 \\ -1 & 1 \end{pmatrix} \), \(B\) memiliki invers, dan \( (AB^{-1})^{-1} = \begin{pmatrix} 1 & -1 \\ 3 & 0 \end{pmatrix} \) maka matriks \(B = \cdots \)

  1. \( \begin{pmatrix} 4 & -1 \\ 6 & 1 \end{pmatrix} \)
  2. \( \begin{pmatrix} 3 & 2 \\ 6 & 9 \end{pmatrix} \)
  3. \( \begin{pmatrix} 2 & 0 \\ 0 & 1 \end{pmatrix} \)
  4. \( \begin{pmatrix} 1 & 6 \\ 4 & 3 \end{pmatrix} \)
  5. \( \begin{pmatrix} 4 & 5 \\ 6 & -5 \end{pmatrix} \)
Pembahasan »

Ingat bahwa sifat perkalian invers pada matriks berlaku: \( (AB)^{-1} = B^{-1} \cdot A^{-1} \) dan \( A^{-1} \cdot A = I \). Dengan demikian, kita peroleh hasil berikut:

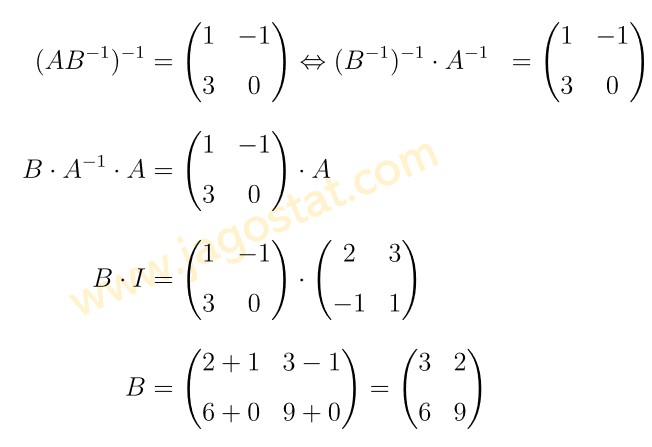
contoh soal invers matriks dan pembahasannya

Jawaban B.

Contoh 4: UNBK Matematika IPS 2019

Diketahui matriks \( A = \begin{pmatrix} 4 & -2 \\ 1 & 5 \end{pmatrix} \), \( B = \begin{pmatrix} 3 & 7 \\ -2 & -4 \end{pmatrix} \) dan \( C = \begin{pmatrix} 7 & -9 \\ 10 & -2 \end{pmatrix} \) memenuhi persamaan \( X = A + 2B-C^T \), dengan \( C^T \) merupakan transpose matriks \(C\). Invers matriks \(X\) adalah…

  1. \( -\frac{1}{15} \begin{pmatrix} -1 & 2 \\ -6 & 3 \end{pmatrix} \)
  2. \( -\frac{1}{15} \begin{pmatrix} -1 & -6 \\ -2 & 3 \end{pmatrix} \)
  3. \( \frac{1}{15} \begin{pmatrix} 1 & 2 \\ 6 & -3 \end{pmatrix} \)
  4. \( \frac{1}{15} \begin{pmatrix} 1 & -2 \\ 6 & 3 \end{pmatrix} \)
  5. \( \frac{1}{15} \begin{pmatrix} 1 & -2 \\ -6 & -3 \end{pmatrix} \)
Pembahasan »

Berdasarkan informasi yang diberikan dalam soal, diperoleh:

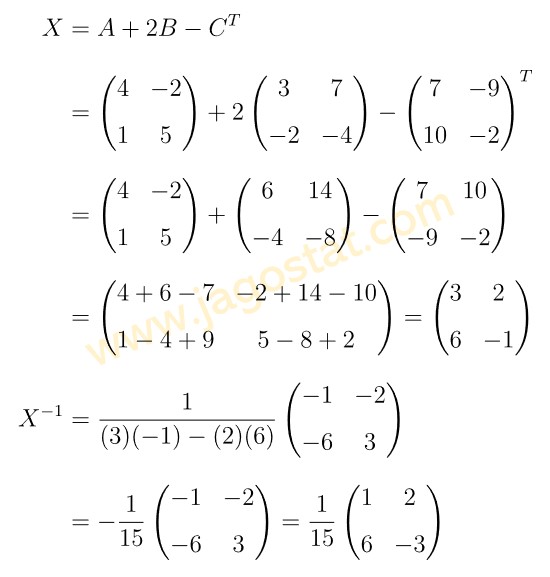
contoh soal invers matriks dan pembahasannya

Jawaban C.

Contoh 5: SPMB 2007

Jika matriks \(X\) memenuhi \( \begin{pmatrix} 2 & 3 \\ 1 & 0 \end{pmatrix} X = \begin{pmatrix} 2 & 1 \\ 0 & 3 \end{pmatrix} \), maka invers dari matriks \(X\) adalah…

  1. \( \begin{pmatrix} 4 & 2 \\ 2 & 1 \end{pmatrix} \)
  2. \( \begin{pmatrix} 5 & 6 \\ 3 & 0 \end{pmatrix} \)
  3. \( \begin{pmatrix} 1 & 6 \\ \frac{1}{2} & -\frac{1}{6} \end{pmatrix} \)
  4. \( \begin{pmatrix} -1 & 0 \\ -\frac{2}{3} & \frac{2}{3} \end{pmatrix} \)
  5. \( \begin{pmatrix} -\frac{5}{6} & -1\frac{1}{2} \\ -\frac{1}{3} & 0 \end{pmatrix} \)
Pembahasan »

Ingat bahwa untuk matriks \( A \cdot B = C \) maka \( B = A^{-1} \cdot C \). Berdasarkan sifat matriks tersebut, kita dapatkan hasil berikut:

contoh soal invers matriks dan pembahasannya

Jawaban E.

Contoh 6: SIMAK UI 2009

Jika \( B = \begin{bmatrix} 3 & -1 \\ -2 & 1 \end{bmatrix} \) dan \( (BA^{-1})^{-1} = \begin{bmatrix} 2 & 1 \\ 4 & 3 \end{bmatrix} \), maka matriks \( A = \cdots \)

  1. \( \begin{bmatrix} 4 & -1 \\ 6 & -1 \end{bmatrix} \)
  2. \( \begin{bmatrix} 1 & 1 \\ 2 & 3 \end{bmatrix} \)
  3. \( \begin{bmatrix} 2 & 0 \\ 0 & 1 \end{bmatrix} \)
  4. \( \begin{bmatrix} 4 & 5 \\ 10 & 13 \end{bmatrix} \)
  5. \( \begin{bmatrix} \frac{3}{2} & -\frac{1}{2} \\ -2 & 1 \end{bmatrix} \)
Pembahasan »

Untuk mengerjakan soal ini, ingat beberapa sifat invers matriks berikut:

\begin{aligned} (AB)^{-1} &= B^{-1} \cdot A^{-1} \\[8pt] (A^{-1})^{-1} &= A \\[8pt] B^{-1} \cdot B &= I \end{aligned}

Berdasarkan sifat invers matriks di atas, kita peroleh berikut ini:

contoh soal invers matriks dan pembahasannya

Jawaban A.

Contoh 7: SPMB 2004 Regional I

Jika matriks \( A = \begin{pmatrix} a & 1-a \\ 0 & 1 \end{pmatrix} \) dan \( A^{-1} = \begin{pmatrix} 2 & b \\ 0 & 1 \end{pmatrix} \) maka nilai \(b\) adalah…

  1. \( -1 \)
  2. \( -\frac{1}{2} \)
  3. \( 0 \)
  4. \( \frac{1}{2} \)
  5. \( 1 \)
Pembahasan »

Ingat bahwa untuk matriks \( A = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \) maka invers matriks \(A\) adalah \( A^{-1} = \frac{1}{ad-bc} \begin{pmatrix} d & -b \\ -c & a \end{pmatrix} \). Dengan demikian, dapat kita tuliskan berikut ini:

contoh soal invers matriks dan pembahasannya

Jadi, nilai \(b\) adalah \(-1\).

Jawaban A.

Contoh 8: SBMPTN 2014 DASAR

Jika \( P = \begin{bmatrix} 1 & 2 \\ 1 & 3 \end{bmatrix}\) dan \( \begin{bmatrix} x & y \\ -z & z \end{bmatrix} = 2P^{-1} \) dengan \( P^{-1} \) menyatakan invers matriks P, maka \(x+y = \cdots\)

  1. 0
  2. 1
  3. 2
  4. 3
  5. 4
Pembahasan »

Pertama, kita cari dulu invers dari matriks P, yakni:

\begin{aligned} P^{-1} &= \frac{1}{1 \cdot 3 - 2 \cdot 1} \begin{bmatrix} 3 & -2 \\ -1 & 1 \end{bmatrix} \\[8pt] &= \begin{bmatrix} 3 & -2 \\ -1 & 1 \end{bmatrix} \end{aligned}

Dengan demikian,

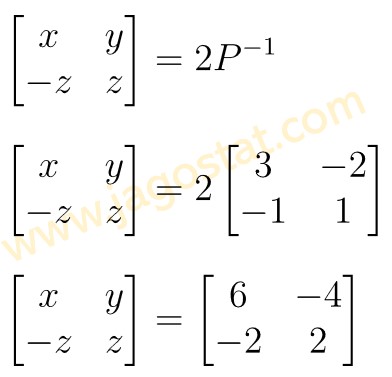
contoh soal invers matriks dan pembahasannya

Dari hasil di atas diperoleh \(x = 6\) dan \(y = -4\) sehingga \(x + y = 6 – 4 = 2\).

Jawaban C.

Contoh 9: UM UGM 2005

Matriks \( \begin{pmatrix} x & 1 \\ -2 & 1-x \end{pmatrix} \) tidak mempunyai invers untuk nilai \(x = \cdots \)

  1. \( -1 \ \text{atau} -2 \)
  2. \( -1 \ \text{atau} 0 \)
  3. \( -1 \ \text{atau} 1 \)
  4. \( -1 \ \text{atau} 2 \)
  5. \( 1 \ \text{atau} 2 \)
Pembahasan »

Ingat bahwa syarat sebuah matriks membuat invers maka determinannya tidak boleh sama dengan nol. Dengan kata lain, jika determinan matriks sama dengan nol, maka matriks tersebut tidak mempunyai invers. Dengan demikian, berdasarkan syarat invers matriks, maka dapat dituliskan berikut ini:

contoh soal invers matriks dan pembahasannya

Jawaban D.

Contoh 10: SPMB 2005 Regional II

Agar matriks \( \begin{pmatrix} p-1 & p+q \\ p-q & p+1 \end{pmatrix} \) mempunyai invers, syaratnya adalah…

  1. \( p \neq 0 \)
  2. \( q \neq 0 \)
  3. \( pq \neq 0 \)
  4. \( p \neq 1 \) dan \( p \neq -1 \)
  5. \( q \neq 1 \) dan \( q \neq -1 \)
Pembahasan »

Syarat sebuah matriks mempunyai invers adalah determinannya tidak sama dengan nol sehingga dapat kita tuliskan berikut ini:

contoh soal invers matriks dan pembahasannya

Jawaban E.

Contoh 11: SPMB 2005 Regional III

Jika \( P = \begin{pmatrix} 1+x & x \\ -x & 1-x \end{pmatrix} \) dan \( P^{-1} \) adalah invers dari \(P\), maka \( (P^{-1})^2 \) sama dengan matriks…

  1. \( \begin{pmatrix} 1+2x & -2x \\ 2x & 1-2x \end{pmatrix} \)
  2. \( \begin{pmatrix} 2x & 1-2x \\ 1+2x & -2x \end{pmatrix} \)
  3. \( \begin{pmatrix} 1-2x & 2x \\ -2x & 1+2x \end{pmatrix} \)
  4. \( \begin{pmatrix} 1+2x & 2x \\ -2x & 1-2x \end{pmatrix} \)
  5. \( \begin{pmatrix} 1-2x & -2x \\ 2x & 1+2x \end{pmatrix} \)
Pembahasan »

Ingat bahwa untuk matriks \( A = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \) maka invers matriks \(A\) adalah \( A^{-1} = \frac{1}{ad-bc} \begin{pmatrix} d & -b \\ -c & a \end{pmatrix} \). Dengan demikian, dapat kita tuliskan berikut ini:

contoh soal invers matriks dan pembahasannya

Jawaban E.

Contoh 12: UM UGM 2014

Nilai semua \(x\) sehingga matriks \( \begin{pmatrix} \sqrt{x^2-1} & 1 \\ x & 2 \end{pmatrix} \) mempunyai invers adalah…

  1. \( x \neq - \frac{4}{3} \) dan \( x \neq \frac{4}{3} \)
  2. \( x \neq -\sqrt{ \frac{4}{3} } \) dan \( x \neq \sqrt{ \frac{4}{3} } \)
  3. \( \sqrt{ \frac{4}{3} } < x \leq -1 \) atau \( 1 \leq x < \sqrt{ \frac{4}{3} } \)
  4. \( -\sqrt{ \frac{4}{3} } < x \leq -1 \) atau \( 1 < x < \sqrt{ \frac{4}{3} } \)
  5. \( x < -\sqrt{ \frac{4}{3} } \) atau \( -\sqrt{ \frac{4}{3} } < x \leq -1 \) atau \( 1 \leq x < \sqrt{ \frac{4}{3} } \) atau \( x > \sqrt{ \frac{4}{3} } \)
Pembahasan »

Ingat bahwa syarat sebuah matriks mempunyai invers adalah determinannya tidak sama dengan nol. Berdasarkan syarat invers matriks ini, kita dapatkan hasil berikut:

contoh soal invers matriks dan pembahasannya

Selanjutnya, syarat agar sebuah fungsi bentuk akar \( \sqrt{ f(x) } \) mempunyai nilai real adalah \( f(x) \geq 0 \). Dalam hal ini, agar \( \sqrt{x^2-1} \) mempunyai nilai real maka \( x^2-a \geq 0 \). Nilai \(x\) yang memenuhi pertidaksamaan kuadrat \( x^2-1 \geq 0 \) adalah \( x \leq -1 \) atau \( x \geq 1 \).

Nilai semua \(x\) yang memenuhi matriks yang diberikan dalam soal adalah irisan dari nilai \(x\) yang diperoleh di atas. Jika kita gambarkan irisan dari \( x \neq \pm \sqrt{ \frac{4}{3} } \) dan \( x \leq -1 \) atau \( x \geq 1 \), maka akan tampak seperti berikut ini:

contoh soal invers matriks dan pembahasannya

Berdasarkan gambar di atas, maka nilai dari semua nilai \(x\) yang memenuhi matriks \( \begin{pmatrix} \sqrt{x^2-1} & 1 \\ x & 2 \end{pmatrix} \) adalah \( x < -\sqrt{ \frac{4}{3} } \) atau \( -\sqrt{ \frac{4}{3} } < x \leq -1 \) atau \( 1 \leq x < \sqrt{ \frac{4}{3} } \) atau \( x > \sqrt{ \frac{4}{3} } \).

Jawaban E.

Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan jika ada yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima Kasih.

Oleh Tju Ji Long · Statistisi

Artikel Terkait
img

Contoh soal dan pembahasan matriks matematika SMA

img

Contoh soal dan pembahasan determinan matriks

The two most important days in your life are the day you are born and the day you find out why.

Mark Twain