
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Bahas Soal Matematika » Pangkat, Akar, & Logaritma › 20 Contoh Soal dan Pembahasan Logaritma Matematika SMA
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552
20 Contoh Soal dan Pembahasan Logaritma Matematika SMA
Pada artikel ini kita akan membahas beberapa contoh soal logaritma matematika SMA yang sering muncul. Ada 20 soal logaritma yang kita bahas di sini. Untuk dapat mengerjakan soal logaritma dengan lancar, kita perlu pahami dulu beberapa sifat logaritma penting berikut ini:

Setelah memahami sifat-sifat logaritma di atas, mari kita ke contoh soal dan pembahasan logaritma berikut ini:
Contoh 1:
Jika \( ^{25} \! \log 5^{2x} = 8 \), maka \( x = \cdots \)
- 1/4
- 1/2
- 6
- 8
- 10
Untuk menyelesaikan soal ini, gunakan sifat logaritma ini:
\begin{aligned} {}^{a^c} \! \log b^d = \frac{d}{c} \cdot {}^a \! \log b \end{aligned}
Penyelesaian dari soal ini, yaitu:

Jawaban D.
Contoh 2:
Diketahui \( {}^5 \! \log 4 = m \). Bentuk \( {}^{25} \! \log 20 \) jika dinyatakan dalam \(m\) adalah…
- \(m+1\)
- \(m+2\)
- \( \frac{1}{2}m+1 \)
- \( \frac{1}{2}m + \frac{1}{2} \)
- \( \frac{1}{2}m - \frac{1}{2} \)
Untuk menyelesaikan soal ini kita bisa gunakan sifat logaritma ini:
\begin{aligned} & {}^a \! \log bc = {}^a \! \log b + {}^a \! \log c \end{aligned}
Penyelesaian dari soal ini, yaitu:

Jawaban D.
Untuk soal-soal selanjutnya di bawah ini kita akan memperingkas pembahasannya tanpa menyebutkan sifat logaritma yang dipakai. Silahkan Anda cermati sendiri sifat logaritma yang digunakan.
Baca juga:
Contoh 3:
Jika diketahui \( {}^2 \! \log 3 = x \), maka nilai \( {}^8 \! \log 12 \) adalah…
- \( \frac{1}{3}(-x-2) \)
- \( \frac{1}{3}(x-2) \)
- \( \frac{1}{3}(x+2) \)
- \( \frac{1}{3}(x+3) \)
- \( \frac{1}{3}(x-3) \)
Penyelesaian dari soal ini, yaitu:
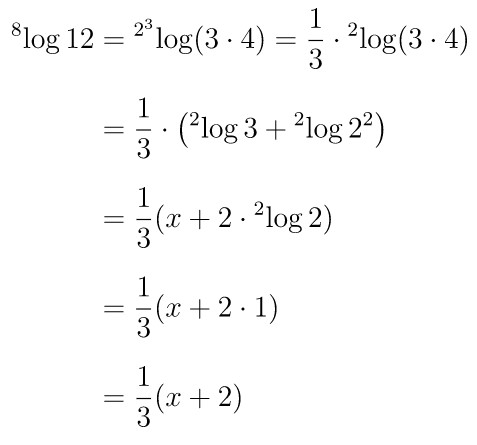
Jawaban C.
Contoh 4:
Jika \( {}^9 \! \log 8 = p \) maka \( \displaystyle {}^4 \! \log \frac{1}{3} = \cdots \)
- \( -\frac{3}{2}p \)
- \( -\frac{3}{4}p \)
- \( -\frac{2}{3}p \)
- \( -\frac{4}{3}p \)
- \( -\frac{6}{4}p \)
Penyelesaian dari soal ini, yaitu:

Jawaban B.
Contoh 5:
Nilai dari \( \displaystyle {}^7 \! \log 4 \cdot {}^2 \! \log 5 + {}^7 \! \log \frac{49}{25} = \cdots \)
- 1
- 2
- 3
- 4
- 5
Penyelesaian dari soal ini, yaitu:

Jawaban B.
Contoh 6:
Nilai \( 3 ( {}^2 \! \log y ) – {}^2 \! \log y^2 + {}^2 \! \log \frac{1}{y} \) adalah…
- \( 1 \)
- \( 0 \)
- \( y \)
- \( -1 \)
- \( -y \)
Penyelesaian dari soal ini, yaitu:
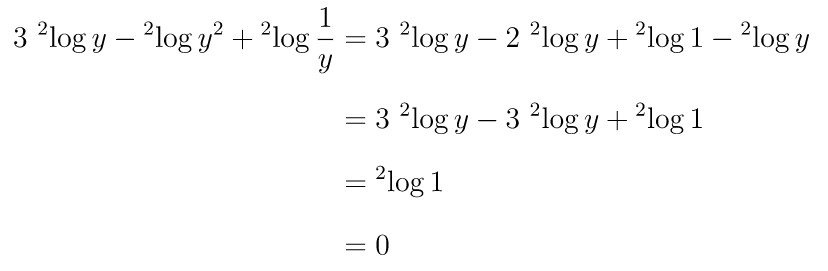
Jawaban B.
Contoh 7:
Jika \( {}^2 \! \log 3 = a \) dan \( {}^3 \! \log 5 = b \) maka \( {}^4 \! \log 45 = \cdots \)
- \( a(b+2) \)
- \( \frac{a}{2}(b+2) \)
- \( \frac{b}{2}(a+2) \)
- \( b(a+2 \)
- \( (a+2)(b+2) \)
Penyelesaian dari soal ini, yaitu:
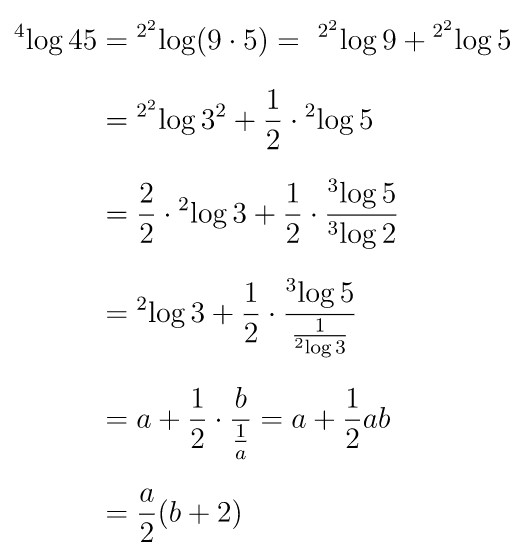
Jawaban B.
Contoh 8:
Hasil dari \( \displaystyle \frac{ {}^3 \! \log 36 \cdot {}^6 \! \log 81 + {}^4 \! \log 32 }{ {}^{\frac{1}{9}} \! \log 27 } \) adalah ….
- \( 11 \)
- \( 7 \)
- \( 4 \)
- \( -7 \)
- \( -11 \)
Penyelesaian dari soal ini, yaitu:

Jawaban D.
Contoh 9:
Bentuk sederhana dari \( \displaystyle \frac{\log p^3 q - 2 \log q + \log p^2 q^6}{3 \log pq} = \cdots \)
- \( \frac{5}{2} \log pq \)
- \( \frac{2}{5} \log pq \)
- \( \frac{2}{5} \)
- \( \frac{3}{5} \)
- \( \frac{5}{3} \)
Penyelesaian dari soal ini, yaitu:

Jawaban E.
Baca juga:
Contoh 10:
Hasil \( \displaystyle \frac{ {}^{\sqrt{3}} \! \log 5 \cdot {}^{25} \! \log 3 \sqrt{3} - {}^4 \! \log 16}{{}^3 \! \log 54-{}^3 \! \log 2} \) adalah…
- \( -\frac{9}{2} \)
- \( -\frac{1}{6} \)
- \( -\frac{1}{3} \)
- \( 3 \)
- \( \frac{9}{2} \)
Penyelesaian dari soal ini, yaitu:

Jawaban B.
Contoh 11:
Nilai \(x\) yang memenuhi \( \displaystyle ({}^4 \! \log x)^2 - {}^2 \! \log \sqrt{x} - \frac{3}{4} = 0 \) adalah…
- 16 atau 4
- 16 atau \( \frac{1}{4} \)
- 8 atau 2
- 8 atau \( \frac{1}{2} \)
- 8 atau 4
Penyelesaian dari soal ini, yaitu:
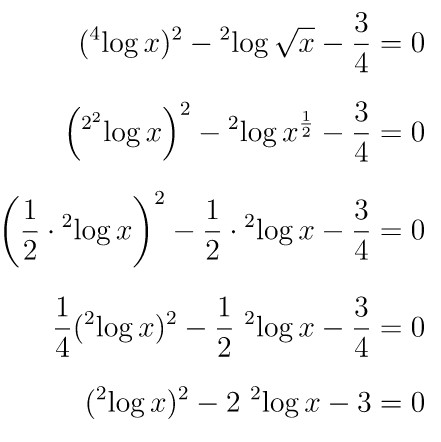
Sekarang misalkan \( {}^2 \! \log x = p \) sehingga persamaan di atas menjadi:

Untuk \(p = 3\), maka
\begin{aligned} {}^2 \! \log x = 3 \Leftrightarrow x = 2^3 = 8 \end{aligned}
Untuk \(p = -1\), maka
\begin{aligned} {}^2 \! \log x = -1 \Leftrightarrow x = 2^{-1} = \frac{1}{2} \end{aligned}
Jadi, nilai \(x\) yang memenuhi adalah 8 atau ½.
Jawaban D.
Contoh 12:
Hasil penjumlahan semua nilai \(x\) yang memenuhi persamaan \( x^{4 \log x} = \frac{x^{12}}{10^8} \) adalah…
- 1
- 11
- 101
- 110
- 1100
Dengan menggunakan beberapa sifat logaritma dan manipulasi aljabar, penyelesaian dari soal di atas kurang lebih seperti berikut ini:

Jawaban D.
Contoh 13:
Diketahui \( {}^p \! \log 2 = 8 \) dan \( {}^q \! \log 8 = 4 \). Jika \( s = p^4 \) dan \( t = q^2 \), maka nilai \( {}^t \! \log 2 = \cdots \)
- 1/4
- 1/3
- 2/3
- 3/2
- 3
Dari soal diketahui bahwa:

Jawaban D.
Contoh 14:
Diketahui \( a = {}^4 \! \log x \) dan \( b = {}^2 \! \log x \). Jika \( {}^4 \! \log b + {}^2 \! \log a =2 \), maka \( a + b \) adalah…
- 4
- 6
- 8
- 12
- 16
Dari soal diketahui bahwa:
\begin{aligned} a &= {}^4 \! \log x = {}^{2^2} \! \log x \\[8pt] &= \frac{1}{2} \ {}^{2} \! \log x = \frac{1}{2}b \\[8pt] b &= 2a \end{aligned}
Dengan demikian,

Jawaban B.
Contoh 15:
Jika \( {}^x \! \log w = \frac{1}{2} \) dan \( {}^{xy} \! \log w = \frac{2}{5} \), maka nilai \( {}^y \! \log w \) adalah…
- 8
- 6
- 4
- 2
- 1
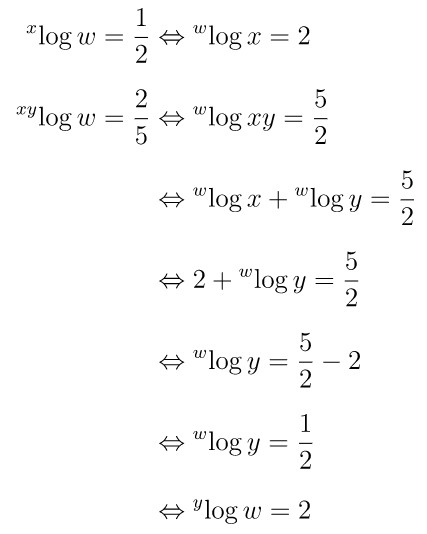
Jawaban D.
Contoh 16:
Sebuah lingkaran memiliki jari-jari \( \log a^2 \) dan keliling \( \log b^4 \), maka \( {}^a \! \log b = \cdots \)
- \( \frac{1}{4\pi} \)
- \( \frac{1}{\pi} \)
- \( \pi \)
- \( 2\pi \)
- \( 10^{2\pi} \)
Rumus keliling lingkaran adalah \( 2 \pi r \), sehingga berlaku:
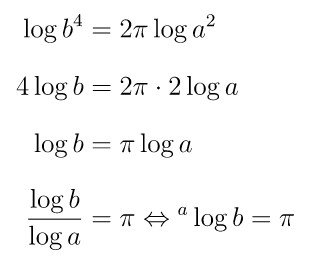
Jawaban C.
Contoh 17:
Jika diketahui \( x = \log a, \ y = \log b \) dan \( z = \log c \), maka bentuk sederhana dari \( \displaystyle \log \left( \frac{a}{b^2} \sqrt{c} \right) \) dalam \(x, y\) dan \(z\) adalah…
- \( \log \left( \frac{x}{y^2} \sqrt{z} \right) \)
- \( \log x - \log y^2 + \log \sqrt{z} \)
- \( \frac{x}{y^2} \sqrt{z} \)
- \( x-2y+\frac{1}{2}z \)
- \( x-y^2+\sqrt{z} \)
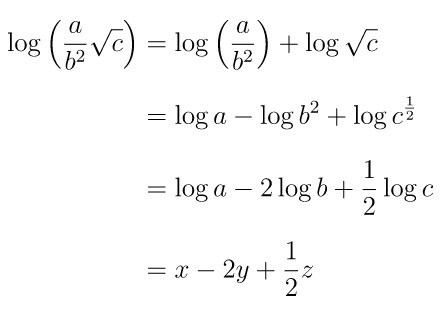
Jawaban D.
Contoh 18:
Nilai \( \displaystyle \frac{\left({}^5 \! \log 10 \right)^2 - \left({}^5 \! \log 2 \right)^2}{ {}^5 \! \log \sqrt{20} } = \cdots \)
- \( \frac{1}{2} \)
- \( 1 \)
- \( 2 \)
- \( 4 \)
- \( 5 \)
Untuk menyelesaikan soal logaritma di atas kita gunakan sifat aljabar berikut:
\[ a^2 – b^2 = (a+b)(a-b) \]
Dengan demikian,

Jawaban C.
Contoh 19:
Jika \( \displaystyle \left( {}^2 \! \log x \right)^2 - \left( {}^2 \! \log y \right)^2 = {}^2 \! \log 256 \) dan \( \displaystyle {}^2 \! \log x^2 - {}^2 \! \log y^2 = {}^2 \! \log 16 \), maka nilai dari \( {}^2 \! \log x^6 y^{-2} \) adalah…
- \( 24 \)
- \( 20 \)
- \( 16 \)
- \( 8 \)
- \( 4 \)
Untuk menyelesaikan persamaan logaritma di atas, kita coba sederhanakan penulisan dengan memisalkan \( {}^2 \! \log x = a \) dan \( {}^2 \! \log y = b \) sehingga dapat kita tuliskan:

Dengan menyelesaikan persamaan \(a-b = 2\) dan \(a+b=4\), kita peroleh \(a = 3\) dan \(b = 1\) sehingga

Jawaban C.
Contoh 20:
Apabila \(x\) dan \( y \) memenuhi \( \log x^2 - \log y = 1 \) dan \( \log x + \log y = 8 \) maka nilai \( y – x = \cdots \)
- \( 9 \)
- \( 99 \)
- \( 990 \)
- \( 9.900 \)
- \( 99.000 \)
Dengan menggunakan beberapa sifat logaritma, maka dapat kita peroleh:


Dengan demikian,

Jawaban E.
Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan jika ada yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Oleh Tju Ji Long · Statistisi
Artikel Terkait
Today I will do what others won't, so tomorrow I can do what others can't.