
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Bahas Soal Matematika » Matriks › Contoh Soal dan Pembahasan Determinan Matriks Matematika SMA
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552
Contoh Soal dan Pembahasan Determinan Matriks Matematika SMA
Salah satu konsep dalam pelajaran matriks yang penting yaitu determinan matriks. Kita bisa menggunakan konsep determinan matriks untuk mencari invers suatu matriks. Pada artikel ini kita akan latihan mengerjakan soal yang berkaitan dengan determinan matriks. Semoga bermanfaat.
Contoh 1: UN 2009
Diketahui matriks \( A = \begin{bmatrix} 1 & 2 \\ 3 & 5 \end{bmatrix}\) dan \( B = \begin{bmatrix} 3 & -2 \\ 1 & 4 \end{bmatrix} \). Jika A’ adalah transpose matriks A dan \( AX = B + A’ \), maka determinan matriks \(X\) adalah…
- 46
- 33
- 27
- -33
- -46
Berdasarkan sifat determinan, \( |AX| = |A||X| \). Dari soal diketahui \( AX = B + A’ \) sehingga kita peroleh berikut ini:

Jawaban D.
Contoh 2: UN 2008
Diketahui matriks \( P = \begin{bmatrix} 2 & 5 \\ 1 & 3 \end{bmatrix} \) dan \( Q = \begin{bmatrix} 5 & 4 \\ 1 & 1 \end{bmatrix} \). Jika \( P^{-1} \) adalah invers matriks P dan \( Q^{-1} \) adalah invers matriks Q, maka determinan dari \( P^{-1} Q^{-1} \) adalah…
- 223
- 1
- -1
- -10
- -223
Pertama, kita cari determinan dari matriks P dan Q terlebih dahulu, yakni:

Selanjutnya, berdasarkan sifat determinan, \( |PQ| = |P||Q| \) dan \( |A^{-1}| = \frac{1}{|A|} \). Dengan demikian, determinan dari \( P^{-1} Q^{-1} \), yaitu:
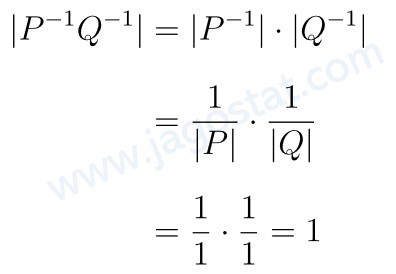
Jawaban B.
Contoh 3: SNMPTN 2010 DASAR
Jika M adalah matriks sehingga \( M \times \begin{bmatrix} a & b \\ c & d \end{bmatrix} = \begin{bmatrix} a & b \\ -a+c & -b+d \end{bmatrix} \), maka determinan matriks M adalah…
- 1
- -1
- 0
- -2
- 2
Determinan dari matriks M, yaitu:
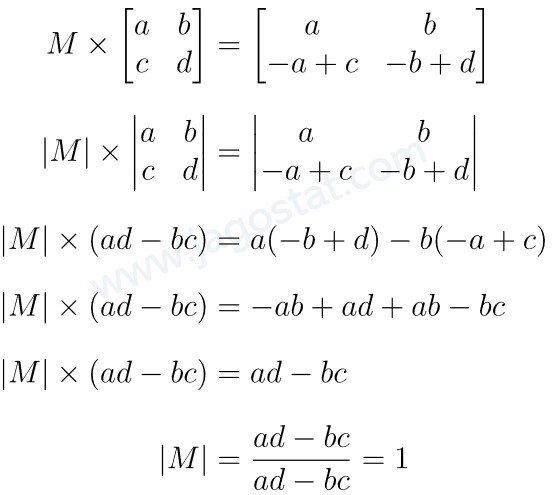
Jawaban A.
Contoh 4: UTBK 2019
Diketahui \( B = \begin{bmatrix} 2 & 0 \\ 0 & 1 \end{bmatrix} \) dan \( B + C = \begin{bmatrix} 2 & 1 \\ -3 & 1 \end{bmatrix} \). Jika A adalah matriks berukuran 2 x 2 sehingga \( AB + AC = \begin{bmatrix} 4 & 2 \\ -3 & 1 \end{bmatrix} \), maka determinan dari AB adalah…
- 4
- 2
- 1
- -1
- -2
Kita cari matriks \(C\) terlebih dahulu, yakni:
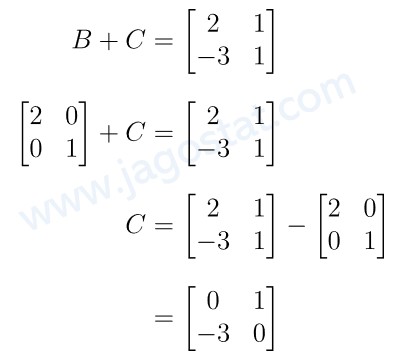
Sekarang, misalkan \( A = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \) sehingga

Selanjutnya, kita cari nilai a, b, c, dan d. Dari hasil di atas diperoleh hubungan berikut:
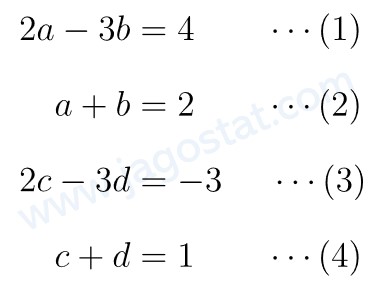
Dari persamaan (1) dan (2) diperoleh nilai a = 2 dan b = 0. Dari persamaan (3) dan (4) diperoleh nilai c = 0 dan d = 1. Jadi, matriks \(A = \begin{bmatrix} a & b \\ c & d \end{bmatrix} = \begin{bmatrix} 2 & 0 \\ 0 & 1 \end{bmatrix} \).
Dengan demikian, determinan matriks AB, yaitu:
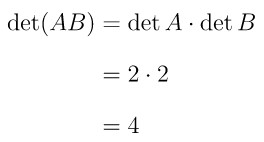
Jawaban A.
Contoh 5: (SNMPTN 2012 DASAR)
Jika \( A = \begin{bmatrix} 2 & 0 \\ 1 & x \end{bmatrix}, \ B = \begin{bmatrix} 1 & 5 \\ 0 & -2 \end{bmatrix} \), dan \( \det(AB) = 12 \), maka nilai \(x\) adalah…
- -6
- -3
- 0
- 3
- 6
Berdasarkan sifat determinan matriks, \( \det(AB) = \det(A) \cdot \det(B) \) sehingga:
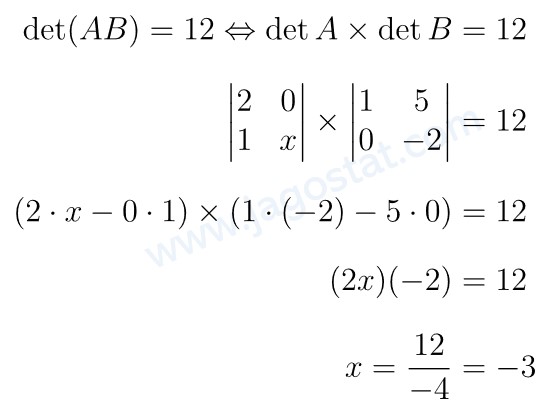
Jawaban B.
Contoh 6: SNMPTN 2012 DASAR
Jika \( AB = \begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix} \) dan \( \det(A) = 2 \) maka \( \det(BA^{-1}) \) adalah…
- 8
- 6
- 4
- 2
- 1
Berdasarkan sifat determinan matriks, \( |AB| = |A| \times |B| \) sehingga:

Dengan demikian,

Jawaban E.
Contoh 7:
Diketahui matriks \( \begin{bmatrix} 3x-1 & x+2 \\ 2 & x \end{bmatrix} \) mempunyai determinan 14. Jumlah semua nilai \(x\) dari matriks tersebut adalah…
- 1/2
- 1
- -2
- 0
- -1/2

Jawaban B.
Contoh 8:
Diketahui matriks \( \begin{bmatrix} x^2-3x & 2x-5 \\ x+1 & x-4 \end{bmatrix} \) tidak mempunyai invers. Hasil kali semua nilai \(x\) dari matriks tersebut adalah…
- -1
- 2
- 4
- -5
- 4
Karena matriks tidak mempunyai invers, maka determinannya bernilai nol, sehingga:

Koefisien dari persamaan polinomial (suku banyak) di atas, yaitu \(a = 1, \ b = -9, \ c = 15\), dan \(d = 5\). Dengan demikian, berdasarkan rumus perkalian akar polinomial, maka hasil kali semua nilai \(x\), yakni:

Jawaban D.
Contoh 9:
Jika \( Q = \begin{bmatrix} a & b \\ c & d \end{bmatrix}, \ P = \begin{bmatrix} 3 & 1 \\ 5 & 2 \end{bmatrix} \), dan \( QP = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \), maka determinan matriks \(Q\) adalah…
- 0
- 10
- 1
- 5
- -3
Berdasarkan sifat determinan matriks, \( |QP| = |Q||P| \) sehingga

Jawaban C.
Contoh 10:
Jika M adalah matriks sehingga \( M \times \begin{bmatrix} p & q \\ r & s \end{bmatrix} = \begin{bmatrix} p+r & q+s \\ -r & -s \end{bmatrix} \), maka determinan matriks M adalah…
- 0
- -1
- 5
- 1
- 2
Dengan menggunakan salah satu sifat determinan matriks, penyelesaian dari soal ini yaitu:

Jawaban B.
Contoh 11:
Transpos matriks \( A = \begin{bmatrix} p & q \\ r & s \end{bmatrix} \) adalah \( A^T = \begin{bmatrix} p & r \\ q & s \end{bmatrix} \). Jika \( A^T = A^{-1} \), maka\( ps-qr = \cdots \)
- \( \frac{1}{2} \) dan \( -\frac{1}{2} \)
- 0 dan 1
- \( \sqrt{2} \) dan \( -\sqrt{2} \)
- -1 dan 0
- -1 dan 1

Jawaban E.
Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan jika ada yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima Kasih.
Oleh Tju Ji Long · Statistisi
Artikel Terkait
Sometimes the wrong choices bring us to the right places.