www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Aljabar Linear » Sistem Persamaan Linear › Aturan Cramer, Contoh Soal dan Pembahasan
Aturan Cramer, Contoh Soal dan Pembahasan
Ada beberapa cara untuk mencari solusi atau penyelesaian dari suatu sistem persamaan linear, salah satunya yaitu menggunakan Aturan Cramer.
Ada beberapa cara untuk mencari solusi atau penyelesaian dari suatu sistem persamaan linear. Salah satu cara yang akan kita bahas di artikel ini dikenal dengan Aturan Cramer atau Kaidah Cramer, diambil dari nama penemunya yakni Gabriel Cramer (1704–1752).
Aturan Cramer digunakan untuk menyelesaikan sistem persamaan linear dengan n persamaan dalam n variabel. Dasar metode ini adalah matriks dan determinan, sehingga kita perlu memahami kedua konsep tersebut terlebih dahulu untuk dapat menerapakan Aturan Cramer dalam mencari solusi suatu sistem persamaan linear.
Agar lebih jelas, kita akan menerapkan Aturan Cramer untuk menyelesaikan sistem persamaan linear dua variabel (SPLDV) dan sistem persamaan linear tiga variabel (SPLTV). Sekarang, perhatikanlah sistem persamaan linear dua variabel berikut.

Kita tahu bahwa dengan menggunakan metode eliminasi, kita peroleh nilai \(x\) sebagai berikut:
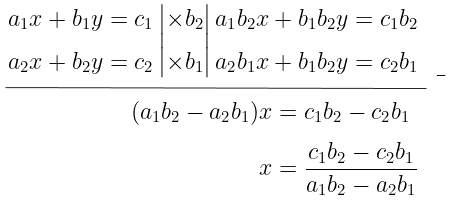
Perhatikan bahwa kita bisa menuliskan hasil yang diperoleh di atas dalam bentuk determinan matriks, yakni:
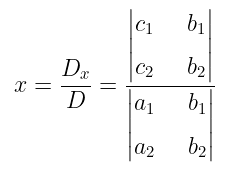
Dengan cara serupa kita peroleh nilai \(y\), yaitu:


Hal yang perlu diingat ialah determinan matriks koefisien \(D\) tidak boleh bernilai nol. Jika \(D=0\), maka nilai \(x\) dan \(y\) menjadi tidak terdefinisi, karena seperti terlihat pada rumus di atas, kita tidak bisa membagi \(Dx\) dan \(Dy\) dengan suatu bilangan nol.
Aturan Cramer juga dapat digunakan untuk menyelesaikan sistem persamaan linear tiga variabel (SPLTV). Misalkan diketahui sistem persamaan linear tiga variabel (SPLTV) sebagai berikut.
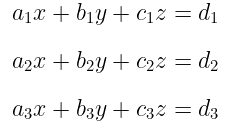
Dengan cara yang sama pada SPLDV, berikut ini adalah solusi dari SPLTV dengan Aturan Cramer:
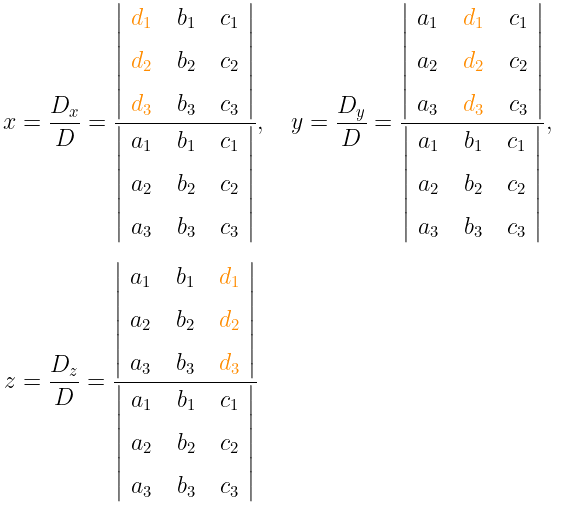
Contoh 1:
Selesaikan sistem persamaan linear dua variabel (SPLDV) berikut dengan menggunakan Aturan Cramer.

Pembahasan:
SPLDV dalam soal di atas dapat dinyatakan dalam bentuk matriks, yakni

Dengan demikian, kita peroleh hasil berikut ini.

Berdasarkan Aturan Cramer, kita peroleh hasil berikut.

Jadi, nilai \(x\) dan \(y\) yang memenuhi SPLDV di atas yaitu \(x = -2\) dan \(y = 3\).
Contoh 2:
Selesaikanlah sistem persamaan linear tiga variabel (SPLTV) berikut dengan menggunakan Aturan Cramer.

Pembahasan:
SPLTV dalam soal di atas dapat dinyatakan dalam bentuk matriks, yakni

Pertama kita cari dulu determinan dari matriks koefisien untuk memastikan apakah Aturan Cramer dapat diterapkan atau tidak. Matriks koefisien dari SPLTV di atas yaitu:

Dengan menggunakan metode ekspansi kofaktor, kita peroleh determinannya yaitu

Karena \(D ≠ 0\), maka Aturan Cramer dapat diterapkan. Selanjutnya, kita cari determinan-determinan lainnya yakni

Dengan demikian, berdasarkan Aturan Cramer, kita peroleh hasil berikut:

Jadi, solusi dari sistem persamaan linear tiga variabel tersebut yaitu \( x = 2, y = 0, \ \) dan \( z = -1 \).
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Showing off is the fool's idea of glory.
