
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Bahas Soal Matematika » Integral › Integral Parsial Trigonometri
Tentukan hasil dari \(\int e^x \sin x \ dx = \cdots ? \)
Pembahasan:
Untuk menyelesaikan soal ini, kita akan gunakan teknik integral parsial. Misalkan \(u = e^x\) dan \(dv = \sin x \ dx\) sehingga diperoleh

Selanjutnya dari hasil di atas, kita peroleh berikut ini:

Untuk melanjutkan hasil di atas, kita perlu menyelesaikan \(\int e^x \cos x \ dx\) terlebih dahulu. Kita bisa selesaikan integral tersebut menggunakan teknik integral parsial dengan memisalkan \(u = e^x\) dan \(dv = \cos x \ dx\) sehingga kita dapatkan berikut ini:
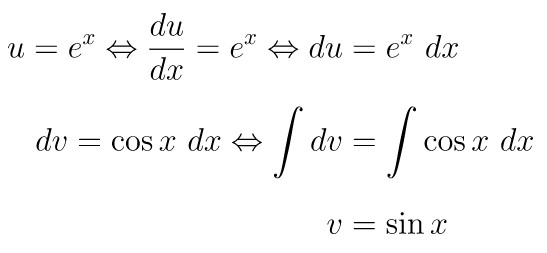
Dengan melanjutkan hasil yang kita peroleh sebelumnya kita peroleh jawaban dari integral pada soal, yaitu:

Baca juga:
\( \displaystyle \int x \ \sin x \ dx = \cdots ? \)
\( \displaystyle \int x \ \cos x \ dx = \cdots ? \)
\( \displaystyle \int x^2 \ \sin x \ dx = \cdots ? \)
\( \displaystyle \int e^x \ \cos x \ dx = \cdots ? \)
\( \displaystyle \int x \ \sin^{-1} x \ dx = \cdots ? \)
\( \displaystyle \int x \ \cos^{-1} x \ dx = \cdots ? \)
\( \displaystyle \int x \ \tan^{-1} x \ dx = \cdots ? \)
\( \displaystyle \int x \ \cot^{-1} x \ dx = \cdots ? \)