www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Geometri › Transformasi Geometri: Translasi (Pergeseran)
Transformasi Geometri: Translasi (Pergeseran)
Translasi atau pergeseran adalah perpindahan titik-titik pada bidang dengan jarak dan arah tertentu yang mana diwakili oleh ruas garis berarah (vektor).
Translasi atau pergeseran adalah perpindahan titik-titik pada bidang dengan jarak dan arah tertentu. Jarak dan arah tertentu itu diwakili oleh ruas garis berarah (vektor). Misalkan \( \overrightarrow{AB} \) atau suatu pasangan bilangan \( \left[ {\begin{array}{rr} a \\ b \end{array} } \right] \), yang berarti pada translasi titik \( (x_1,y_1) \) oleh \( \left[ {\begin{array}{rr} a \\ b \end{array} } \right] \), absis titik ditambah dengan a, sedangkan ordinatnya ditambah dengan b.

Gambar 1. Translasi titik A ke A'
Perhatikan Gambar 1. Suatu translasi T yang dinyatakan dengan komponen \( \left[ {\begin{array}{rr} a \\ b \end{array} } \right] \) akan memetakan titik \( A(x_1,y_1) \) ke titik \( A'(x_1+a,y_1+b) \) yang dinotasikan dengan:
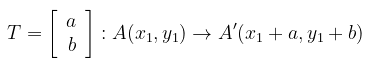
Contoh Soal dan Pembahasan
Berikut ini diberikan beberapa contoh soal dan pembahasan mengenai transformasi geometri khususnya yang berkaitan dengan translasi atau pergeseran.
Contoh 1:
Tentukanlah bayangan (peta) titik A(4,3) oleh translasi \( T = \left[ {\begin{array}{rr} 3 \\ 2 \end{array} } \right] \).
Pembahasan:
Bentuk umum translasi titik \( A(x_1,y_1) \) oleh \( T = \left[ {\begin{array}{rr} a \\ b \end{array} } \right] \) adalah

Dengan demikian,
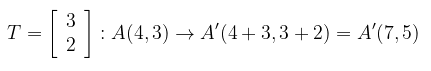
Jadi, bayangan hasil translasi dengan titik koordinat baru A'(7,5).
Contoh 2:
Titik A(1,-2) ditranslasikan oleh \( T = \left( {\begin{array}{rr} a \\ b \end{array} } \right) \) dipetakan menjadi titik A'(4,3). Tentukanlah T.
Pembahasan:
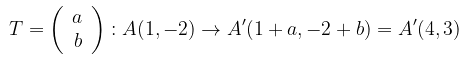
Dengan demikian,

Jadi, \( T = \left( {\begin{array}{rr} 3 \\ 5 \end{array} } \right) \).
Contoh 3:
Tentukanlah bayangan persamaan lingkaran \( x^2 + y^2 = 16 \) oleh translasi \( T = \left( {\begin{array}{rr} -1 \\ 2 \end{array} } \right) \).
Pembahasan:
Diketahui persamaan lingkaran:
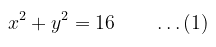
Karena translasi \( T = \left( {\begin{array}{rr} -1 \\ 2 \end{array} } \right) \), maka
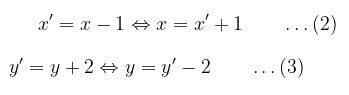
Persamaan (2) dan (3) disubstitusikan ke (1) sehingga

Jadi, bayangan persamaannya adalah
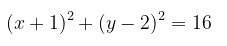
Sumber:
Sunardi, Slamet Waluyo & Sutrisna. 2014. Konsep dan Penerapan Matematika SMA/MA Kelas XI. Jakarta: Penerbit PT Bumi Aksara.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
The best time to plant a tree was 20 years ago. The second best time is today.
