www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Geometri › Transformasi Geometri: Refleksi (Pencerminan)
Transformasi Geometri: Refleksi (Pencerminan)
Suatu refleksi ditentukan oleh suatu garis tertentu sebagai sumbu pencerminan. Hal yang perlu diperhatikan pada pencerminan adalah jarak bangun mula-mula ke sumbu pencerminan sama dengan jarak bangun bayangannya ke sumbu pencerminan.
Pernahkan Anda memerhatikan diri Anda saat Anda bercermin? Bagaimanakah bentuk dan ukuran tubuh Anda? Bayangan Anda pada cermin sama bentuk dan ukurannya dengan diri Anda sebenarnya. Hal ini merupakan bentuk nyata peristiwa pencerminan (refleksi) dalam kehidupan sehari-hari.
Suatu refleksi ditentukan oleh suatu garis tertentu sebagai sumbu pencerminan. Hal yang perlu diperhatikan pada pencerminan adalah jarak bangun mula-mula ke sumbu pencerminan sama dengan jarak bangun bayangannya ke sumbu pencerminan.
Sekarang, amati Gambar 1 berikut ini.
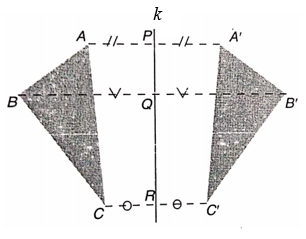
Gambar 1. Refleksi ΔABC terhadap garis \(k\)
Dari Gambar 1 di atas, tampak bahwa ΔABC dicerminkan terhadap garis \( l \) menghasilkan \(ΔA'B'C'\). Perhatikan bahwa
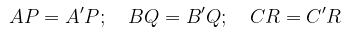
Jadi, dengan mengamati Gambar 1 di atas, diketahui bahwa pada pencerminan berlaku sifat-sifat sebagai beriku.
- Bangun bayangan sebelum dengan bangun mula-mula.
- Keliling bangun bayangannya sama dengan keliling bangun mula-mula.
- Luas bangun bayangannya sama dengan luas bangun mula-mula.
Ada berbagai jenis pencerminan suatu titik, seperti diilustrasikan pada Gambar 2 di bawah.
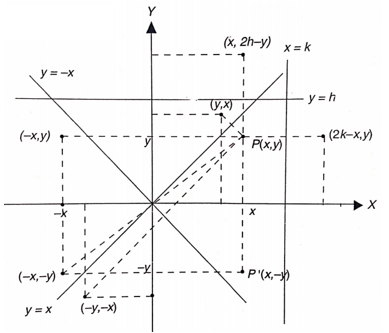
Gambar 2. Berbagai jenis pencerminan titik P(x,y) terhadap berbagai sumbu pencerminan.
Pada Gambar 2, salah satu pencerminan titik P(x,y) adalah pencerminan terhadap sumbu x menghasilkan titik P'(x',y') sehingga:

atau dapat juga dinyatakan dalam bentuk matriks:
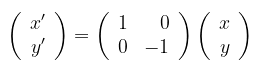
Dengan demikian, titik \(P(x,y) \to P'(x',y')\) ditentukan oleh persamaan matriks:
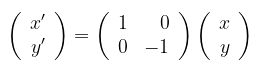
Jadi, matriks \( \left( {\begin{array}{rr} 1 & 0 \\ 0 & -1 \end{array} } \right) \) adalah matriks yang bersesuaian dengan transformasi pencerminan terhadap sumbu x.
Dengan cara yang sama seperti contoh di atas, dapat diperoleh persamaan matriks dari suatu pencerminan titik P(x,y) terhadap berbagai sumbu pencerminan seperti tercantum pada Tabel 1 berikut.

Contoh Soal dan Pembahasan
Untuk lebih memahami transformasi geometri khususnya terkait refleksi atau pencerminan, perhatikan beberapa contoh soal dan pembahasan berikut ini.
Contoh 1:
Diketahui segitiga ABC dengan titik-titik sudut A(1,1), B(4,2), dan C(2,3).
- Tentukan peta ΔABC jika dicerminkan terhadap sumbu y!
- Gambarlah ΔABC dan petanya pada koordinat Cartesius!
Pembahasan:
- Matriks transformasi pencerminan terhadap sumbu y adalah
- Titik sudut ΔABC disusun ke bentuk matriks, yaitu . Misalkan bayangan ΔABC setelah pencerminan terhadap sumbu y adalah \( A'(x_1',y_1'), B'(x_2',y_2'), C'(x_3',y_3') \), atau dalam bentuk matriks dituliskan:
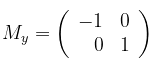
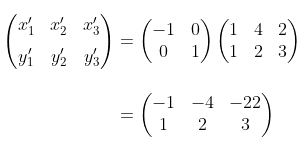
Jadi, bayangan ΔABC adalah ΔA'B'C', dengan A'(-1,1), B'(-4,2), dan C'(-2,3). Sehingga gambar ΔABC dan bayangannya pada koordinat Cartesius dapat dilihat pada Gambar berikut.
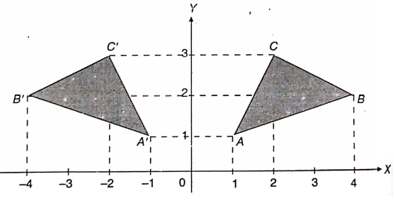
Gambar 1. Refleksi ΔABC terhadap sumbu \(y\)
Sumber:
Sunardi, Slamet Waluyo & Sutrisna. 2014. Konsep dan Penerapan Matematika SMA/MA Kelas XI. Jakarta: Penerbit PT Bumi Aksara.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Don't just teach your children to read, teach them to question what they read. Teach them to question everything.
