www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Geometri › Transformasi Geometri: Dilatasi (Perkalian)
Transformasi Geometri: Dilatasi (Perkalian)
Suatu transformasi yang mengubah ukuran (memperbesar atau memperkecil) suatu bangun, tetapi tidak mengubah bentuk bangun tersebut disebut dilatasi (perkalian). Suatu dilatasi ditentukan oleh titik pusat dilatasi dan faktor dilatasi (faktor skala).
Pernahkan Anda melihat maket atau miniatur rumah di televisi, koran, atau pameran? Maket atau miniatur rumah/gedung merupakan model dari rumah atau gedung sebenarnya, tetapi dibuat dalam ukuran lebih kecil. Dengan kata lain, rumah atau gedung yang sebenarnya dilakukan transformasi dilatasi diperkecil dalam bentuk maket atau miniatur.
Suatu transformasi yang mengubah ukuran (memperbesar atau memperkecil) suatu bangun, tetapi tidak mengubah bentuk bangun disebut dilatasi (perkalian). Suatu dilatasi ditentukan oleh titik pusat dilatasi dan faktor dilatasi (faktor skala).
Perhatikan ilustrasi dilatasi diperbesar dan diperkecil dengan pusat dilatasi di \(O(0,0)\) dan faktor dilatasi \(k\) pada Gambar 1 berikut:
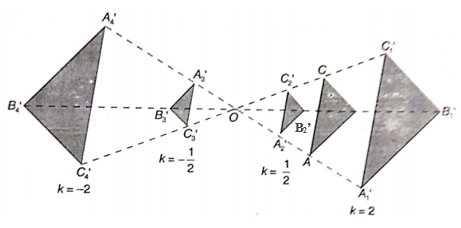
Gambar 1. Dilatasi dengan pusat O(0,0)
Dilatasi yang berpusat di titik koordinat \(O(0,0)\) dengan faktor dilatasi \(k\) dilambangkan \(D[O,k]\), sedangkan dilatasi yang berpusat di sembarang titik \(P(x,y)\) dengan faktor dilatasi \(k\) dilambangkan \(D[P,k]\) atau \([(a,b),k]\). Sebagai contoh, Gambar 1 mengilustrasikan dilatasi ABC yang berpusat di titik \(O(0,0)\) dengan berbagai faktor skala \(k\). Pada Gambar 1, \(D[O,k]\) memetakan segitiga ABC ke segitiga lain sebagai berikut.
- Untuk \(k = 2, D[0,2]: ΔABC \to A_1'B_1'C_1' \)
- Untuk \( k = \frac{1}{2}, D\left[0,\frac{1}{2}\right]: ΔABC \to A_2'B_2'C_2' \)
- Untuk \( k = - \frac{1}{2}, D\left[0,-\frac{1}{2}\right]: ΔABC \to A_3'B_3'C_3' \)
- Untuk \(k = -2, D[0,-2]: ΔABC \to A_4'B_4'C_4' \)
Berdasarkan nilai dari faktor dilatasi k, bangun hasil (bayangan) yang diperoleh dapat ditetapkan sebagai berikut:
- Jika \(k > 1\), maka bangun hasil terletak sepihak dari pusat dilatasi dengan bangun mula-mula dan diperbesar.
- Jika \(0 < k < 1\), maka bangun hasil terletak sepihak dari pusat dilatasi dengan bangun mula-mula dan diperkecil.
- Jika \(-1 < k < 0\), maka bangun hasil terletak berlainan pihak dari pusat dilatasi dengan bangun mula-mula dan diperkecil.
- Jika \(k < - 1\), maka bangun hasil terletak berlainan pihak dari pusat dilatasi dengan bangun mula-mula dan diperbesar.
Jadi, dengan mengamati Gambar 1 di atas, pada dilatasi \(D[O,k]\) juga diperoleh sifat-sifa sebagai berikut:
- Bangun bayangan sebangun dengan bangun mula-mula.
- Keliling bangun bayangannya = \(k\) x keliling bangun mula-mula.
- Luas bangun bayangannya = \( k^2 \) x luas bangun mula-mula.
Dilatasi terhadap Titik Pusat O(0,0)
Perhatikan Gambar 2. Pada Gambar 2, titik \(P(x,y)\) didilatasikan terhadap titik pusat \(O\) dengan faktor dilatasi \(k\), menghasilkan titik \(P'(x',y')\), sehingga
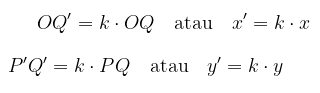
Gambar 2. Dilatasi dengan [O,k]
Jadi, dilatasi \([O,k]\) memetakan titik \(P(x,y)\) ke \(P'(kx,ky)\) atau

Bentuk matriks transformasi dari \(D[O,k]\) diperoleh dari
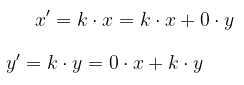
Sehingga,
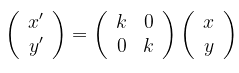
Agar lebih jelas, mari kita perhatikan beberapa contoh soal berikut ini.
Contoh 1:
Tentukanlah bayangan dari \(ΔABC\) yang dibentuk oleh titik-titik sudut A(-1,4), B(-3,-1), dan C(2,3), bila didilatasikan oleh pusat dilatasi O(0,0) dengan faktor dilatasi 2.
Pembahasan:
Misalkan bayangan titik-titik A, B, dan C berturut-turut adalah \( A'(x_1',y_1'), B'(x_2',y_2'), C'(x_3',y_3') \), maka
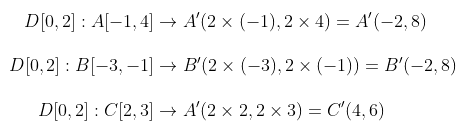
Titik A', B', dan C' juga dapat ditentukan dengan menggunakan matriks transformasi:
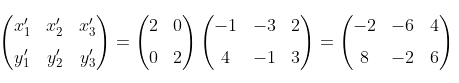
Jadi, bayangan ΔABC adalah ΔA'B'C' dengan A'(-2,8), B'(-6,-2), dan C'(4,6).
Dilatasi terhadap Pusat (a,b)
Amati Gambar 3. Pada Gambar 3, diperoleh hubungan sebagai berikut. Jika titik P(x,y) didilatasikan oleh \( D[(a,b),k] \) akan diperoleh bayangan \( P'(x',y') \).
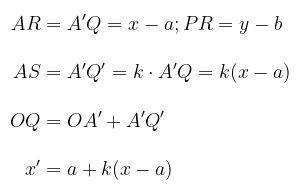
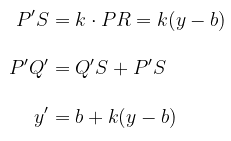
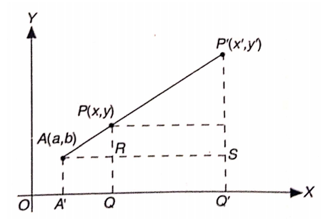
Gambar 3. Dilatasi terhadap pusat (a,b)
Jadi,
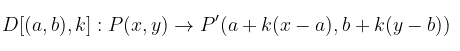
Bentuk matriks transformasi dari \( D[(a,b),k] \) diperoleh dengan cara sebagai berikut:
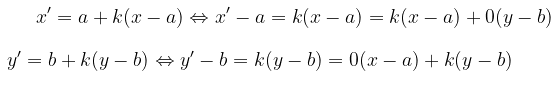
Jadi, matriks transformasi dilatasi dengan pusat (a,b) dan faktor dilatasi k adalah
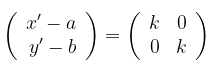
Sehingga, didapatkan persamaan matriks:
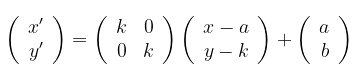
Contoh 2:
Tentukanlah bayangan dari \(ΔABC\) jika titik-titik sudut A(-1,4), B(2,3), dan C(3,-2) didilatasikan oleh \( D[(1,2), -2] \).
Pembahasan:
Misalkan bayangan titik A(-1,4), B(2,3), dan C(3,-2) oleh D[(1,2), -2] berturut-turut adalah \( A'(x_1',y_1'), B'(x_2',y_2'), C'(x_3',y_3') \). Titik-titik A', B', C' ditentukan sebagai berikut.
- Untuk \( A'(x_1',y_1') \) yaitu bayangan dari titik A(-1,4):
- Untuk \( B'(x_2',y_2') \) yaitu bayangan dari titik B(2,3):
- Untuk \( C'(x_3',y_3') \) yaitu bayangan dari titik C(3,-2):
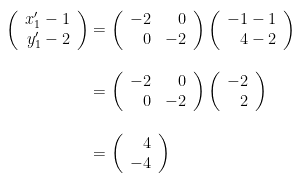
Sehingga:

Jadi, diperoleh titik A'(5,-2).
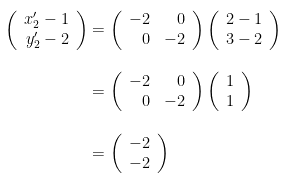
Sehingga:

Jadi, diperoleh titik B'(-1,0).
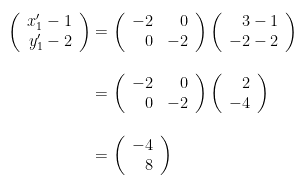
Sehingga:

Jadi, diperoleh titik C'(-3,10).
Sumber:
Sunardi, Slamet Waluyo & Sutrisna. 2014. Konsep dan Penerapan Matematika SMA/MA Kelas XI. Jakarta: Penerbit PT Bumi Aksara.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
If you're curious, you find lots of interesting things to do.
