www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Geometri › Transformasi Geometri: Rotasi (Perputaran)
Transformasi Geometri: Rotasi (Perputaran)
Rotasi ditentukan oleh pusat perputaran, besar sudut putar, dan arah sudut putar. Suatu perputaran pada bidang datar mempunyai arah positif bila arah perputaran itu berlawanan arah dengan arah putar jarum jam.
Rotasi atau perputaran ditentukan oleh pusat perputaran, besar sudut putar, dan arah sudut putar. Suatu perputaran pada bidang datar mempunyai arah positif bila arah perputaran itu berlawanan arah dengan arah putar jarum jam. Sedangkan arah negatif terjadi bila arah perputaran itu searah dengan arah putar jarum jam.
Sekarang, amati Gambar 1 berikut.
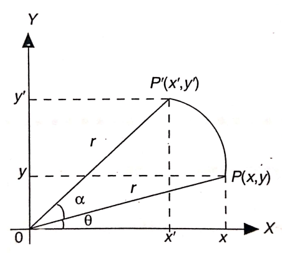
Gambar 1. Rotasi terhadap O sebesar \(α\) radian
Pada Gambar 1, titik \(P'(x',y')\) adalah peta dari titik \(P(x,y)\) oleh rotasi terhadap O sebesar \(α\) radian. Misalkan jika koordinat Cartesius titik \( P(x,y) \) ditulis dengan koordinat kutub menjadi titik \( P(r,θ) \) maka terdapat hubungan
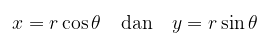
Titik \( P(x,y) = P(r,\theta) \) diputar sebesar \( \alpha \) radian terhadap titik pusat O(0,0) menghasilkan \( P'(x',y') = P'(r,\theta+\alpha) \) sehingga
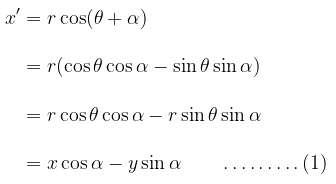
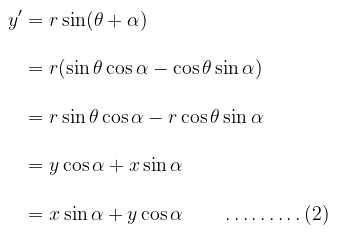
Dari persamaan (1) dan (2), kita peroleh
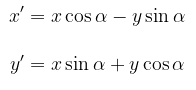
atau dapat dinyatakan dalam bentuk matriks, yaitu
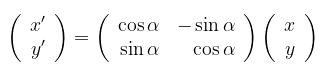
Jadi, jika titik \( P(x,y) \) diputar dengan pusat O sebesar \( \alpha \) radian akan menjadi titik \( P'(x',y') \) dengan:
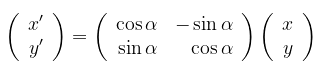
Bentuk matriks
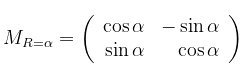
adalah matriks rotasi dengan pusat O sebesar \( \alpha \) radian.
Dengan cara yang sama, jika titik \(P(x,y)\) pada Gambar 2 di bawah diputar dengan pusat \(A(a,b)\) sebesar \( \alpha \) radian maka akan menjadi titik \(P'(x',y')\) dengan:
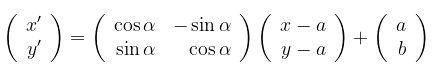
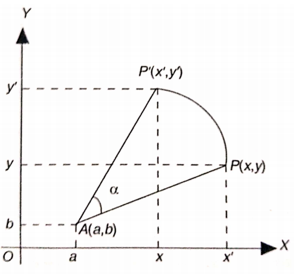
Gambar 2. Rotasi dengan pusat A(a,b) sebesar \( α \) radian
Dalam hal ini, \(P\) ditranslasi oleh \(\left( {\begin{array}{rr} -a \\ -b \end{array} } \right)\), kemudian menjadi \( (x-a, y-b) \), lalu dirotasi oleh \( α, \left( {\begin{array}{rr} \cos α & -\sin α \\ \sin α & \cos α \end{array} } \right) \), dan ditranslasi lagi oleh \(\left( {\begin{array}{rr} a \\ b \end{array} } \right)\) sehingga dihasilkan \( P'(x',y') \).
Untuk lebih jelasnya, perhatikan contoh soal berikut.
Contoh Soal dan Pembahasan
Berikut ini diberikan beberapa contoh soal dan pembahasan mengenai transformasi geometri khususnya yang berkaitan dengan rotasi.
Contoh 1:
Tentukanlah bayangan ΔABC dengan titik sudut A(0,2), B(4,1), dan C(3,6) jika diputar dengan pusat O sebesar \( -\frac{1}{2} π \) radian!
Pembahasan:
Titik-titik sudut ΔABC dapat dibentuk dalam matriks
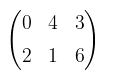
Misalkan bayangan ΔABC yang terbentuk oleh rotasi sebesar \( -\frac{1}{2} π \) dengan sudut pusat O, yaitu \( A'(x_1',y_1'), B'(x_2',y_2'), C'(x_3',y_3') \) dinyatakan dalam bentuk matriks:
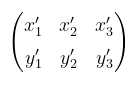
Dengan demikian,
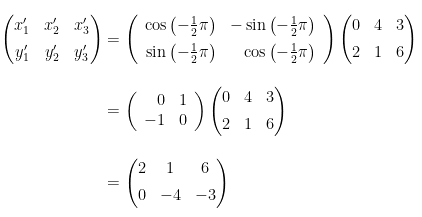
Jadi, bayangan ΔABC adalah ΔA'B'C' dengan A'(2,0), B'(1,-4), dan C'(6,-3).
Contoh 2:
Tentukanlah persamaan bayangan garis \( 2x-y+8 = 0 \) setelah dirotasikan pada pangkal koordinat dengan sudut putaran 900.
Pembahasan:
Matriks rotasi dengan pusat atau pangkal koordinat sebesar 900, ditulis
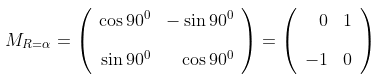
Dengan demikian,
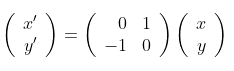
sehingga diperoleh:
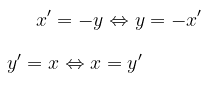
Substitusikan x dan y ke persamaan garis.
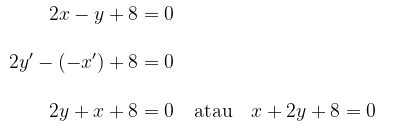
Jadi, bayangannya adalah \( x + 2y + 8 = 0 \).
Sumber:
Sunardi, Slamet Waluyo & Sutrisna. 2014. Konsep dan Penerapan Matematika SMA/MA Kelas XI. Jakarta: Penerbit PT Bumi Aksara.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Not all of us can do great things. But we can do small things with great love.
