www.jagostat.com

www.jagostat.com

Website Belajar Matematika & Statistika

Website Belajar Matematika & Statistika

Matematika Dasar › Matriks › Latihan Soal dan Pembahasan Matriks Bagian 2
Joki Tugas Matematika Murah, Hanya Rp10-20 Ribu. Hub. WA: 0812-5632-4552

Latihan Soal dan Pembahasan Matriks Bagian 2



Soal No 1:

Diketahui matriks A, B, dan C sebagai berikut:

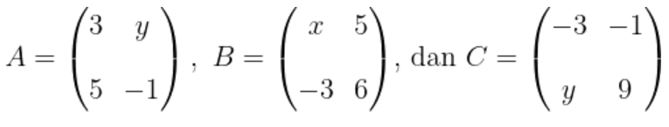
contoh soal matriks

Tentukanlah nilai \(x+2xy+y\) jika

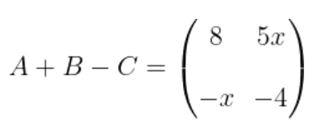contoh soal matriks Pembahasan »

Dari soal, matriks A, B, dan C telah diketahui sehingga diperoleh sebagai berikut:

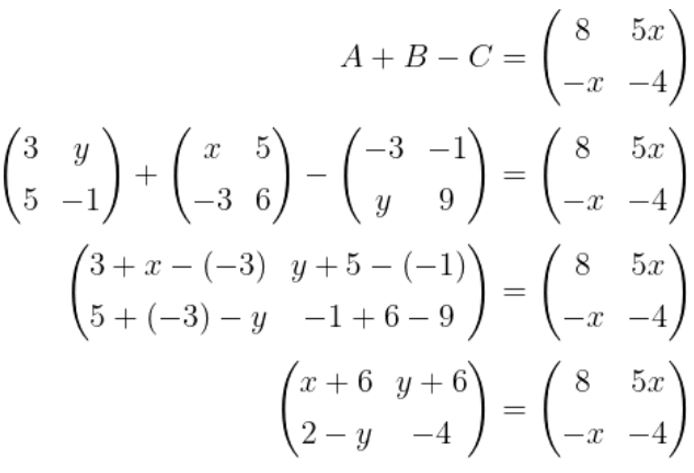
contoh soal matriks

Dari persamaan terakhir ini diperoleh:

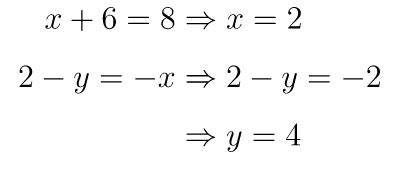
contoh soal matriks

Dengan demikian, nilai \(x + 2xy+y = 2 + 2(2)(4) + 4 = 22\).

Soal No 2:

Diketahui matriks

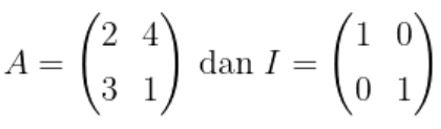
contoh soal matriks

Matriks \((A-kI)\) adalah matriks singular untuk nilai \(k = …\)

Pembahasan »

Pertama, cari dulu matriks \((A-kI)\), yakni:

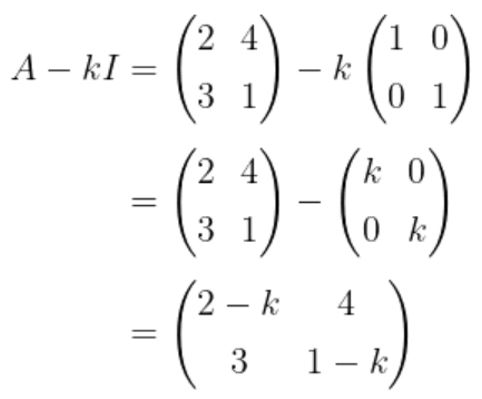
contoh soal matriks

Matriks ini akan singular apabila determinannya 0. Jadi, kita peroleh

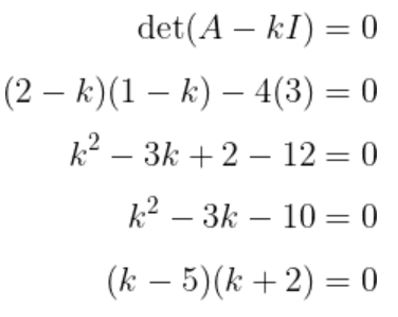
contoh soal matriks

Dari persamaan terakhir ini diperoleh bahwa nilai \(k\) yang memenuhi adalah \(k = -2\) atau \(k = 5\).

Soal No 3:

Diketahui matriks A dan B sebagai berikut:

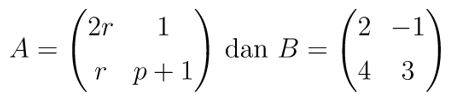
contoh soal matriks

di mana \(r≠0\) dan \(p≠0\). Tentukan nilai \(p\) agar matriks BA tidak memiliki invers.

Pembahasan »

Pertama, kita cari dulu matriks BA, yakni:

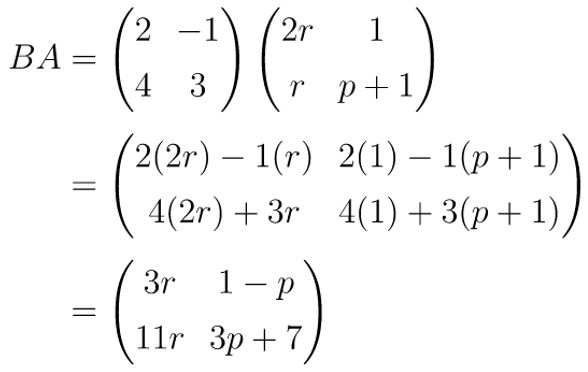
contoh soal matriks

Suatu matriks dikatakan tidak memiliki invers jika determinannya bernilai nol. Dengan demikian, kita peroleh

contoh soal matriks

Selanjutnya bagi kedua ruas dengan \(r\), sehingga diperoleh

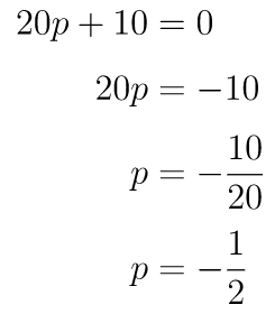
contoh soal matriks

Jadi, nilai \(p\) yang memenuhi adalah \(-1/2\).

Soal No 4: UM UGM 2019

Jika \( A = \begin{pmatrix} 1 & 2 \\ 0 & 1 \\ 1 & 1 \end{pmatrix} \) dan \( B = \begin{pmatrix} 1 \\ 2 \end{pmatrix} \), maka determinan dari \( A^T A + BB^T \) adalah…

  1. -5
  2. -4
  3. 0
  4. 4
  5. 5
Pembahasan »

Kita tentukan matriks dari \( A^T A + BB^T \) terlebih dahulu, yakni:

\begin{aligned} A^T A + BB^T &= \begin{pmatrix} 1 & 2 \\ 0 & 1 \\ 1 & 1 \end{pmatrix}^T \begin{pmatrix} 1 & 2 \\ 0 & 1 \\ 1 & 1 \end{pmatrix} + \begin{pmatrix} 1 \\ 2 \end{pmatrix} \begin{pmatrix} 1 \\ 2 \end{pmatrix}^T \\[8pt] &= \begin{pmatrix} 1 & 0 & 1 \\ 2 & 1 & 1 \end{pmatrix} \begin{pmatrix} 1 & 2 \\ 0 & 1 \\ 1 & 1 \end{pmatrix} + \begin{pmatrix} 1 \\ 2 \end{pmatrix} \begin{pmatrix} 1 & 2 \end{pmatrix} \\[8pt] &= \begin{pmatrix} 2 & 3 \\ 3 & 6 \end{pmatrix} + \begin{pmatrix} 1 & 2 \\ 2 & 4 \end{pmatrix} \\[8pt] &= \begin{pmatrix} 3 & 5 \\ 5 & 10 \end{pmatrix} \end{aligned}

Dengan demikian, determinan dari matriks \( A^T A + BB^T \), yaitu:

\begin{aligned} |A^T A + BB^T| &= \begin{vmatrix} 3 & 5 \\ 5 & 10 \end{vmatrix} \\[8pt] &= 3 \cdot 10 - 5 \cdot 5 \\[8pt] &= 5 \end{aligned}

Jawaban E.

Soal No 5: UM UGM 2019

Diberikan empat matriks A, B, C, dan D masing-masing berukuran 2x2 dengan \( A+CB^T = CD \). Jika A mempunyai invers serta diketahui \( \det(D^T-B) = m \) dan \( \det C = n \), maka \( \det(2A^{-1}) = \cdots \)

  1. \( \frac{4}{mn} \)
  2. \( \frac{mn}{4} \)
  3. \( \frac{4m}{n} \)
  4. \( 4mn \)
  5. \( \frac{m+n}{4} \)
Pembahasan »

Dari soal diketahui \( \det(D^T-B) = m \) dan \( \det C = n \) sehingga:

\begin{aligned} A+CB^T &= CD \Leftrightarrow A = CD-CB^T \\[8pt] |A| &= |CD-CB^T| \Leftrightarrow |A| = | C(D-B^T) | \\[8pt] |A| &= |C| \cdot |(D-B^T)| \\[8pt] |A| &= n \cdot | (D^T-B)^T | \\[8pt] |A| &= n \cdot m \\[8pt] |2A^{-1}| &= 2^2 \cdot |A^{-1}| = 4 \cdot \frac{1}{|A|} \\[8pt] &= \frac{4}{mn} \end{aligned}

Jawaban A.

Soal No 6: UM UGM 2019

Jika \( A= \begin{pmatrix} 1 & x \\ y & z \end{pmatrix} \) dan \(k\) merupakan skalar sehingga \( A + kA^T = \begin{pmatrix} -1 & 5 \\ -7 & -2 \end{pmatrix} \) maka \( x + y + z = \cdots \)

  1. 3
  2. 4
  3. 5
  4. 6
  5. 7
Pembahasan »
\begin{aligned} A + kA^T &= \begin{pmatrix} -1 & 5 \\ -7 & -2 \end{pmatrix} \\[8pt] \begin{pmatrix} 1 & x \\ y & z \end{pmatrix} + k\begin{pmatrix} 1 & x \\ y & z \end{pmatrix}^T &= \begin{pmatrix} -1 & 5 \\ -7 & -2 \end{pmatrix} \\[8pt] \begin{pmatrix} 1 & x \\ y & z \end{pmatrix} + k \begin{pmatrix} 1 & y \\ x & z \end{pmatrix} &= \begin{pmatrix} -1 & 5 \\ -7 & -2 \end{pmatrix} \\[8pt] \begin{pmatrix} 1+k & x+ky \\ y+kx & z+kz \end{pmatrix} &= \begin{pmatrix} -1 & 5 \\ -7 & -2 \end{pmatrix} \end{aligned}

Dari kesamaan matriks di atas, kita peroleh:

\begin{aligned} 1+k=-1 \Leftrightarrow k &= -2 \\[8pt] z+kz =-2 \Leftrightarrow z-2z &=-2 \\[8pt] z &= 2 \\[8pt] x+ky=5 \Leftrightarrow x-2y &= 5 \quad \cdots(1) \\[8pt] y+kx=-7 \Leftrightarrow y-2x &= -7 \quad \cdots(2) \end{aligned}

Dengan menyelesaikan persamaan (1) dan (2) di atas kita peroleh \( x = 3 \) dan \( y = -1 \) sehingga:

\begin{aligned} x+y+z &= 3-1+2 \\[8pt] &= 4 \end{aligned}

Jawaban B.

Soal No 7: UM UNDIP 2019

Diberikan dua buah matriks \( M = \begin{pmatrix} a+b & a \\ b & a-b \end{pmatrix} \) dan \( N = \begin{pmatrix} 1 & -\frac{1}{2}a \\ -2b & 3 \end{pmatrix} \). Jika \( M^t = N \), dengan \( M^t \) menyatakan transpose matriks M, maka nilai \(a\) adalah…

  1. -2
  2. -1
  3. 0
  4. 1
  5. 2
Pembahasan »

Dari soal diketahui \( M^t = N \) sehingga kita peroleh berikut ini:

\begin{aligned} M^t = N \Leftrightarrow \begin{pmatrix} a+b & a \\ b & a-b \end{pmatrix}^T &= \begin{pmatrix} 1 & -\frac{1}{2}a \\ -2b & 3 \end{pmatrix} \\[8pt] \begin{pmatrix} a+b & b \\ a & a-b \end{pmatrix} &= \begin{pmatrix} 1 & -\frac{1}{2}a \\ -2b & 3 \end{pmatrix} \\[8pt] a+b &= 1 \\ a-b &= 3 \\[8pt] 2a &= 4 \Leftrightarrow a = 2 \end{aligned}

Jawaban E.

Soal No 8: SPMB 2007

Jika matriks \( A = \begin{pmatrix} 2 & 0 \\ 4 & 1 \end{pmatrix} \) sehingga \( A^2-2A+I \) adalah…

  1. \( \begin{pmatrix} 1 & 0 \\ 8 & 0 \end{pmatrix} \)
  2. \( \begin{pmatrix} 1 & 0 \\ 4 & 0 \end{pmatrix} \)
  3. \( \begin{pmatrix} 1 & 1 \\ 5 & 0 \end{pmatrix} \)
  4. \( \begin{pmatrix} 1 & 1 \\ 13 & 1 \end{pmatrix} \)
  5. \( \begin{pmatrix} 1 & 1 \\ 9 & 1 \end{pmatrix} \)
Pembahasan »
\begin{aligned} A^2-2A+I &= \begin{pmatrix} 2 & 0 \\ 4 & 1 \end{pmatrix}^2 - 2 \begin{pmatrix} 2 & 0 \\ 4 & 1 \end{pmatrix} + \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \\[8pt] &= \begin{pmatrix} 2 & 0 \\ 4 & 1 \end{pmatrix}\begin{pmatrix} 2 & 0 \\ 4 & 1 \end{pmatrix}- \begin{pmatrix} 4 & 0 \\ 8 & 2 \end{pmatrix} + \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \\[8pt] &= \begin{pmatrix} 4 & 0 \\ 12 & 1 \end{pmatrix} - \begin{pmatrix} 4 & 0 \\ 8 & 2 \end{pmatrix} + \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \\[8pt] &= \begin{pmatrix} 4-4+1 & 0-0+0 \\ 12-8+0 & 1-2+1 \end{pmatrix} \\[8pt] &= \begin{pmatrix} 1 & 0 \\ 4 & 0 \end{pmatrix} \end{aligned}

Jawaban B.

Soal No 9:

Jika \( A = \begin{pmatrix} 1 & 2 \\ 4 & 3 \end{pmatrix} \) dan \( B = \begin{pmatrix} 2 & 3 \\ 0 & 1 \end{pmatrix} \), maka determinan dari matriks \( (A+B)^2 \) adalah…

  1. -3
  2. -2
  3. 0
  4. 2
  5. 3
Pembahasan »

Ingat sifat determinan berikut: \( |A^n| = |A|^n \). Determinan dari matriks \( (A+B)^2 \), yaitu:

\begin{aligned} |(A+B)^2| &= \left | \left[ \begin{pmatrix} 1 & 2 \\ 4 & 3 \end{pmatrix} + \begin{pmatrix} 2 & 3 \\ -1 & 2 \end{pmatrix} \right]^2 \right | = \left | \begin{pmatrix} 3 & 5 \\ 3 & 5 \end{pmatrix}^2 \right | \\[8pt] &= \left( \begin{vmatrix} 3 & 5 \\ 3 & 5 \end{vmatrix} \right)^2 = (3 \cdot 5 - 5 \cdot 3)^2 \\[8pt] &= 0 \end{aligned}

Jawaban C.

Soal No 10: UM UGM 2006

Apabila \(x\) dan \(y\) memenuhi persamaan matriks \( \begin{pmatrix} 1 & -2 \\ -1 & 3 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} -1 \\ 2 \end{pmatrix} \) maka \(x+y \cdots \)

  1. 1
  2. 2
  3. 3
  4. 4
  5. 5
Pembahasan »

Ingat bahwa untuk \( A \cdot B = C \) maka \( B = A^{-1} \cdot C \) sehingga kita peroleh:

\begin{aligned} \begin{pmatrix} 1 & -2 \\ -1 & 3 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} &= \begin{pmatrix} -1 \\ 2 \end{pmatrix} \\[8pt] \begin{pmatrix} x \\ y \end{pmatrix} &= \begin{pmatrix} 1 & -2 \\ -1 & 3 \end{pmatrix}^{-1} \begin{pmatrix} -1 \\ 2 \end{pmatrix} \\[8pt] &= \frac{1}{1 \cdot 3 -(-2) \cdot (-1)} \begin{pmatrix} 3 & 2 \\ 1 & 1 \end{pmatrix} \begin{pmatrix} -1 \\ 2 \end{pmatrix} \\[8pt] &= \frac{1}{3-2} \begin{pmatrix} -3+4 \\ -1+2 \end{pmatrix} \\[8pt] &= \begin{pmatrix} 1 \\ 1 \end{pmatrix} \end{aligned}

Dari kesamaan matriks di atas kita peroleh \( x = 1 \) dan \( y = 1\) sehingga \( x + y = 2 \).

Jawaban B.

Soal No 11: SPMB 2006 (Regional III)

Jika \( A = \begin{pmatrix} x+y & x \\ -1 & x-y \end{pmatrix} \) dan \( B = \begin{pmatrix} 1 & \frac{1}{2}x \\ -2y & 3 \end{pmatrix} \) di mana B adalah transpose dari matriks A, maka \( x^2+(x+y)+(xy)+y^2 = \cdots \)

  1. 1
  2. 2
  3. 3
  4. 4
  5. 5
Pembahasan »

Dari soal kita ketahui bahwa matriks B merupakan transpose dari matriks B, atau \(B = A^T\), sehingga berlaku:

\begin{aligned} B = A^T \Leftrightarrow \begin{pmatrix} 1 & \frac{1}{2}x \\[8pt] -2y & 3 \end{pmatrix} &= \begin{pmatrix} x+y & x \\[8pt] -1 & x-y \end{pmatrix}^T \\[8pt] \begin{pmatrix} 1 & \frac{1}{2}x \\[8pt] -2y & 3 \end{pmatrix} &= \begin{pmatrix} x+y & -1 \\[8pt] x & x-y \end{pmatrix} \\[8pt] \frac{1}{2}x = -1 \Leftrightarrow x &= -2 \\[8pt] -2y=x \Leftrightarrow -2y &=-2 \\[8pt] y &= 1 \end{aligned}

Dengan demikian,

\begin{aligned} x^2+(x+y)+(xy)+y^2 &= (-2)^2+(-2+1)+(-2 \cdot 1) + 1^2 \\[8pt] &= 4+(-1)+(-2)+1 \\[8pt] &= 4-1-2+1 \\[8pt] &= 2 \end{aligned}

Jawaban B.

Soal No 12: SPMB 2006 (Regional II)

Jika \( x = 1, \ y = -1 \) dan \( z = 2 \) adalah soluasi sistem persamaan linear \( \begin{pmatrix} a & b & -3 \\ -2 & -b & c \\ a & 3 & -c \end{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} -3 \\ -1 \\ -3 \end{pmatrix} \), maka nilai \( a^2-bc = \cdots \)

  1. 1
  2. 2
  3. 3
  4. 4
  5. 5
Pembahasan »
\begin{aligned} \begin{pmatrix} a & b & -3 \\ -2 & -b & c \\ a & 3 & -c \end{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix} &= \begin{pmatrix} -3 \\ -1 \\ -3 \end{pmatrix} \\[8pt] \begin{pmatrix} a & b & -3 \\ -2 & -b & c \\ a & 3 & -c \end{pmatrix} \begin{pmatrix} 1 \\ -1 \\ 2 \end{pmatrix} &= \begin{pmatrix} -3 \\ -1 \\ -3 \end{pmatrix} \\[8pt] \begin{pmatrix} a-b-6 \\ -2+b+2c \\ a-3-2c \end{pmatrix} &= \begin{pmatrix} -3 \\ -1 \\ -3 \end{pmatrix} \\[8pt] a-b-6 = -3 \Leftrightarrow a-b &= 3 \quad \cdots (1) \\[8pt] -2+b+2c=-1 \Leftrightarrow b+2c &= 1 \quad \cdots (2) \\[8pt] a-3-2c = -3 \Leftrightarrow a-2c &= 0 \\[8pt] a &= 2c \quad \cdots (3) \end{aligned}

Dari ketiga persamaan di atas, kita peroleh berikut ini:

\begin{aligned} b+2c= 1 \Leftrightarrow a+b &= 1 \\ a-b &= 3 \\[8pt] 2a = 4 \Leftrightarrow a &= 2 \\[8pt] a+b=1 \Leftrightarrow 2+b &= 1 \\[8pt] b &= -1 \\[8pt] 2c = a \Leftrightarrow 2c &= 2 \\[8pt] c &= 1 \\[8pt] a^2-bc = 2^2-(-1)(1) &= 5 \end{aligned}

Jawaban E.

Soal No 13: SPMB 2006 (Regional I)

Jika \( A = \begin{pmatrix} a & b \\ b & x \end{pmatrix} \) dan \( B = \begin{pmatrix} bx & a \\ b & x \end{pmatrix} \), maka jumlah kuadrat semua akar persamaan \( \det A = \det B \) adalah…

  1. \( \left( \frac{a}{b} \right)^2 - 2(a-b) \)
  2. \( \left( \frac{b}{a} \right)^2 -2(a-b) \)
  3. \( \left( \frac{a}{b} \right)^2 - 2(b-a) \)
  4. \( \left( \frac{b}{a} \right)^2 -2(b-a) \)
  5. \( \frac{b}{a} - 2(b-a) \)
Pembahasan »

Untuk menyelesaikan soal ini kita ingat kembali bahwa untuk persamaan kuadrat \( ax^2+bx+c=0 \) yang akar-akarnya \( x_1 \) dan \( x_2 \) maka berlaku:

\begin{aligned} x_1 + x_2 &= -\frac{b}{a} \\[8pt] x_1 \cdot x_2 &= \frac{c}{a} \\[8pt] x_1^2 + x_2^2 &= (x_1+x_2)^2 - 2x_1 \cdot x_2 \end{aligned}

Selanjutnya, karena \( \det A = \det B \), maka

\begin{aligned} \det A = \det B \Leftrightarrow \begin{vmatrix} a & b \\ b & x \end{vmatrix} &= \begin{vmatrix} bx & a \\ b & x \end{vmatrix} \\[8pt] ax-b^2 &= bx^2-ab \\[8pt] bx^2-ax + b^2-ab &= 0 \\[8pt] x_1^2+x_2^2 &= (x_1+x_2)^2-2x_1 \cdot x_2 \\[8pt] &= \left( -\frac{-a}{b} \right)^2 - 2 \left( \frac{b^2-ab}{b} \right) \\[8pt] &= \left( \frac{a}{b} \right)^2 - 2 \left( b-a \right) \end{aligned}

Jawaban C.

Soal No 14: UM UGM 2018 MATDAS

Jika matriks \( \begin{pmatrix} {}^4 \! \log 2^x & 1 \\ {}^2 \! \log 4^y & x \end{pmatrix} \) tidak mempunyai invers dan \( x^2 + y^2 = 32 \) maka nilai \( {}^x \! \log y = \cdots \)

  1. 1
  2. 2
  3. 3
  4. 4
  5. 5
Pembahasan »

Ingat bahwa matriks yang tidak mempunyai invers berarti determinannya sama dengan nol, sehingga kita peroleh:

\begin{aligned} \begin{vmatrix} {}^4 \! \log 2^x & 1 \\[8pt] {}^2 \! \log 4^y & x \end{vmatrix} &= 0 \\[8pt] ({}^4 \! \log 2^x) \cdot x - 1 \cdot {}^2 \! \log 4^y &= 0 \\[8pt] ({}^{2^2} \! \log 2^x) \cdot x - {}^2 \! \log (2^2)^y &= 0 \\[8pt] \left( \frac{x}{2} \cdot {}^2 \! \log 2 \right) \cdot x - 2y \cdot {}^2 \! \log 2 &= 0 \\[8pt] \frac{x^2}{2} - 2y &= 0 \\[8pt] \frac{x^2}{2} = 2y \Leftrightarrow x^2 &= 4y \end{aligned}

Dari soal diketahui \( x^2 + y^2 = 32 \) dan karena \( x^2 = 4y \) maka

\begin{aligned} x^2 + y^2 = 32 \Leftrightarrow 4y + y^2 &= 32 \\[8pt] y^2 + 4y - 32 &= 0 \\[8pt] (y+8)(y-4) &= 0 \\[8pt] y = -8 \ \text{atau} \ y &= 4 \end{aligned}

Karena yang ditanya adalah \( {}^x \! \log y \), maka berdasarkan syarat logaritma, \( y \) harus \( \leq 0 \). Ini berarti \( y = -8 \) tidak memenuhi syarat dan \( y \) yang memenuhi adalah 4 sehingga:

\begin{aligned} x^2 = 4y \Leftrightarrow x^2 &= 4 \cdot 4 \\[8pt] x^2 &= 16 \\[8pt] x &= \pm 4 \end{aligned}

Ingat bahwa dari syarat basis logaritma, \(a > 0 \) dan \(a \neq 1 \) yang berarti \( x = -4 \) tidak memenuhi syarat sehingga \( x = 4 \) dan \( {}^x \! \log y = {}^4 \! \log 4 = 1 \).

Jawaban A.

Soal No 15: UM UGM 2015 MATDAS

Diberikan matriks \( P = \begin{pmatrix} 2 & -1 \\ 4 & 3 \end{pmatrix} \) dan \( Q = \begin{pmatrix} 2r & 1 \\ r & p+1 \end{pmatrix} \) dengan \( r \neq 0 \) dan \( p \neq 0 \). Matriks PQ tidak mempunyai invers apabila nilai \( p = \cdots \)

  1. -3/2
  2. -1/2
  3. -1/4
  4. 1/2
  5. 8/7
Pembahasan »

Ingat bahwa matriks yang tidak mempunyai invers memiliki determinan bernilai nol sehingga:

\begin{aligned} |PQ| = 0 \Leftrightarrow \left | \begin{pmatrix} 2 & -1 \\ 4 & 3 \end{pmatrix} \begin{pmatrix} 2r & 1 \\ r & p+1 \end{pmatrix} \right | &= 0 \\[8pt] \begin{vmatrix} 3r & 1-p \\[8pt] 11r & 3p+7 \end{vmatrix} &= 0 \\[8pt] 3r \cdot (3p+7)-(1-p)(11r) &= 0 \\[8pt] 9pr+21r-11r+11pr &= 0 \\[8pt] 20 pr + 10 r &= 0 \\[8pt] 20p = -10 \Leftrightarrow p &= -\frac{1}{2} \end{aligned}

Jawaban B.

Soal No 16: SIMAK UI 2010 MATDAS

Diketahui matriks \( A = \begin{pmatrix} 1 & -2 \\ 2 & 5 \end{pmatrix} \). Nilai \( k \) yang memenuhi \( k \cdot \det(A^T) = \det(A^{-1}) \) adalah…

  1. 81
  2. 9
  3. 1
  4. 1/9
  5. 1/81
Pembahasan »
\begin{aligned} A^T = \begin{pmatrix} 1 & -2 \\ 2 & 5 \end{pmatrix}^T &= \begin{pmatrix} 1 & 2 \\ -2 & 5 \end{pmatrix} \\[8pt] A^{-1} = \begin{pmatrix} 1 & -2 \\ 2 & 5 \end{pmatrix}^{-1} &= \frac{1}{5+4} \begin{pmatrix} 5 & -2 \\ 2 & 1 \end{pmatrix} \\[8pt] A^{-1} &= \begin{pmatrix} \frac{5}{9} & -\frac{2}{9} \\[8pt] \frac{2}{9} & \frac{1}{9} \end{pmatrix} \\[8pt] k \cdot \det(A^T) &= \det(A^{-1}) \\[8pt] k (5+4) &= \frac{5}{9} \cdot \frac{1}{9}-\left( -\frac{2}{9} \right) \cdot \frac{2}{9} \\[8pt] 9k &= \frac{5}{81}+\frac{4}{81} \Leftrightarrow 9k = \frac{1}{9} \\[8pt] k &= \frac{1}{81} \end{aligned}

Jawaban E.

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.

Artikel Terkait
img

Definisi, notasi, dan operasi matriks

img

Determinan matriks ukuran 2x2 dan 3x3

img

Invers matriks ukuran 2x2 dan 3x3