www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar › Barisan dan Deret › Latihan Soal dan Pembahasan Barisan dan Deret Geometri
Latihan Soal dan Pembahasan Barisan dan Deret Geometri
Salah satu cara agar dapat memahami barisan geometri dengan lebih cepat adalah dengan banyak mengerjakan latihan soal. Agar bisa mengerjakan soal dengan baik, pahami dulu beberapa rumus terkait barisan dan deret geometri berikut:

Berikut ini diberikan beberapa contoh soal terkait barisan dan deret geometri beserta pembahasannya. Semoga bermanfaat!
Contoh 1:
Diketahui barisan geometri dengan suku ke-5 adalah 162 dan suku ke-2 adalah -6. Rasio barisan tersebut adalah...
- -2
- -3
- -4
- -5
- -6
Diketahui \( U_5 = 162 \) dan \( U_2 = -6 \). Dengan melakukan perbandingan antarsuku, maka kita peroleh:
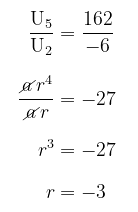
Jawaban B.
Contoh 2:
Berikut ini diberikan beberapa rumus umum suku ke-\(n\) suatu barisan yaitu:
- \( U_n = 4^n - 5 \)
- \( U_n = 2^n \cdot n^{-2} \)
- \( U_n = 2n^3 - 1 \)
- \( U_n = n^3 \cdot 2^{-n} \)
- \( U_n = 2^{n+1} \cdot 3^{-n} \)
Tentukanlah mana yang termasuk rumus umum suku ke-\(n\) untuk barisan geometri berdasarkan rumus di atas.
Pembahasan »Ingat bahwa barisan geometri memiliki rumus umum suku ke-\(n\) yaitu \( U_n = ar^{n-1} \). Perhatikan bahwa rumus barisan geometri hanya terdiri dari 1 suku. Dengan kata lain, tidak ada penjumlahan dan pengurangan.
Jadi, rumus pertama dan ketiga bukan termasuk barisan geometri karena memiliki dua suku dan ada pengurangan.
Selain itu, rumus kedua dan keempat juga bukan termasuk barisan geometri karena variabel \(n\) muncul dengan posisi yang berbeda yaitu sebagai pangkat dan basis.
Dengan demikian, tersisa rumus kelima yang merupakan barisan geometri. Perhatikan bahwa kita bisa menuliskan kembali rumus tersebut menjadi:
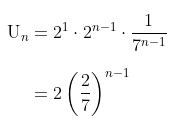
Bentuk rumus terakhir ini menunjukkan barisan geometri dengan suku pertama adalah \(a = 2\) dan rasio \( r = \dfrac27\).
Contoh 3:
Pertumbuhan bakteri mengikuti pola barisan geometri. Setiap satu detik bakteri berkembang biak menjadi 2 kali lipat dari jumlah bakteri sebelumnya. Jika pada saat permulaan terdapat 5 bakteri, maka jumlah bakteri berkembang menjadi 320 bakteri setelah...
- 5 detik
- 6 detik
- 7 detik
- 8 detik
- 9 detik
Dari pernyataan: setiap satu detik bakteri berkembang biak menjadi 2 kali lipat dari jumlah bakteri sebelumnya, maka dapat kita simpulkan bahwa rasio barisan geometri adalah (\(r\)) = 2. Selain itu, dari pernyataan: pada saat permulaan terdapat 5 bakteri, maka dapat disimpulkan bahwa suku pertama adalah \(a = 5\). Dan jumlah bakteri berkembang menjadi 320 bakteri sehingga kita peroleh suku ke-\(n\) yaitu \( U_n = 320 \).
Soal tersebut menanyakan pada detik ke berapa bakteri berkembang menjadi 320 bakteri atau dengan kata lain ditanyakan berapa nilai \(n\). Kita peroleh sebagai berikut:

Jadi, jumlah bakteri berkembang menjadi 320 bakteri setelah 6 detik.
Jawaban B.
Contoh 4:
Diketahui barisan geometri dengan suku pertama adalah 24 dan suku ke-3 adalah 8/3. Tentukanlah suku ke-5 barisan tersebut.
- 8/3
- 8/9
- 8/18
- 8/27
- 8/36
Diketahui suku pertama \(a = 24\) dan \( U_3 = \dfrac83 \). Kita cari rasio barisan geometri terlebih dahulu, yakni:
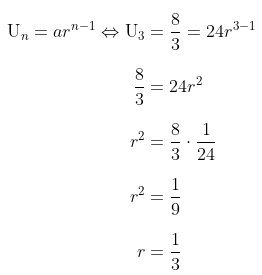
Dengan demikian, suku ke-5 barisan tersebut adalah:
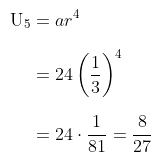
Jawaban D.
Contoh 5:
Jumlah 10 suku pertama dari deret geometri \( 16-8+4-2+\cdots \) adalah...
- 231/8
- 345/9
- 341/32
- 338/7
- 340/6
Dari barisan tersebut diketahui \(a = 16\) dan rasio nya yaitu \( r = -\frac{1}{2} \). Dengan demikian, jumlah 10 suku pertamanya dapat dihitung sebagai berikut:
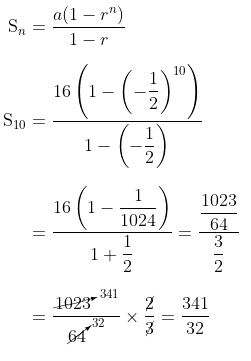
Jadi, jumlah 10 suku pertama deret geometri tersebut adalah \( \frac{341}{32} \).
Jawaban C.
Contoh 6:
Pada sebuah deret geometri, rumus jumlah suku ke-\(n\) nya adalah \(Sn = 2n^2 + 4n\). Tentukan nilai suku ke-9 dari deret tersebut.
- 38
- 39
- 48
- 49
- 59
Jika diketahui jumlah nilai suku-suku suatu barisan geometri, maka untuk mencari suku ke-\(n\) dapat digunakan rumus berikut:
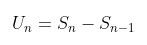
Jumlah nilai 9 suku pertamanya, yaitu:
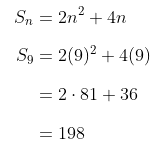
Jumlah nilai 8 suku pertamanya, yaitu:
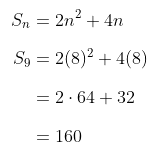
Dengan demikian, nilai dari suku ke-9, adalah:
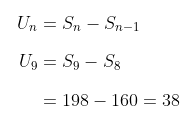
Jawaban A.
Contoh 7:
Diketahui suku keenam dari suatu deret geometri adalah 162. Jumlah logaritma suku kedua, ketiga, keempat, dan kelima sama dengan \( 4 \log 2 + 6 \log 3 \). Rasionya adalah...
- 1
- 2
- 3
- 4
- 5
Diketahui suku ke-6, yaitu:

Karena jumlah logaritma suku kedua, ketiga, keempat, dan kelima sama dengan \( 4 \log 2 + 6 \log 3 \), maka kita peroleh:
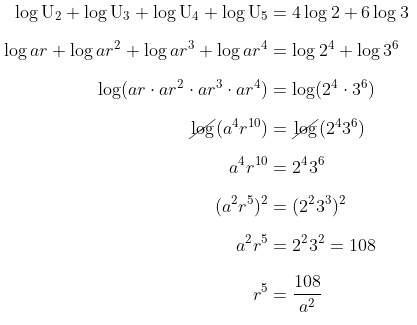
Substitusi hasil yang diperoleh di atas pada \( ar^5 = 162 \). Kita peroleh:
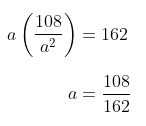
Dengan demikian, rasionya dapat diperoleh sebagai berikut:
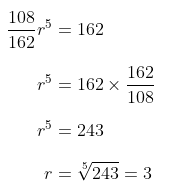
Jawaban C.
Contoh 8:
Tiga bilangan membentuk barisan geometri. Jumlah ketiga bilangan itu adalah 26 dan hasil kalinya 216. Jumlah bilangan pertama dan ketiga dari barisan geometri itu adalah...
- 10
- 20
- 30
- 40
- 50
Pertama, misalkan bahwa ketiga bilangan itu membentuk barisan geometri dalam bentuk \( \frac{a}{r}, \ a, \ ar \) maka hasil kalinya, yaitu:
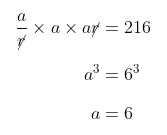
Barisan geometri tersebut sekarang dapat dituliskan sebagai:
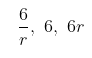
Jumlah ketiga bilangan tersebut adalah 26, sehingga diperoleh:
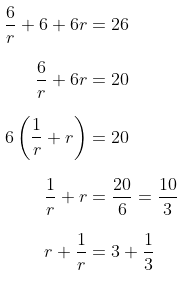
Persamaan terakhir ini menunjukkan bahwa \(r = 3\) atau \(r = 1/3\). Untuk \(a = 6\) dan \(r = 3\), maka barisan geometrinya yaitu 2, 6, 18.
Dan untuk \(a = 6\) dan \(r = 1/3\), maka barisan geometrinya adalah 18, 6, 2.
Jadi, jumlah bilangan pertama dan ketiganya sama meskipun posisinya ditukar, yaitu:
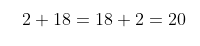
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Stop being afraid of what could go wrong and start being positive about what could go right.
