www.jagostat.com

www.jagostat.com

Website Belajar Matematika & Statistika

Website Belajar Matematika & Statistika

Matematika Dasar › Barisan dan Deret › Latihan Soal Barisan dan Deret Geometri dan Jawabannya
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552

Latihan Soal Barisan dan Deret Geometri dan Jawabannya

Salah satu cara agar dapat memahami barisan geometri dengan lebih cepat adalah dengan banyak mengerjakan latihan soal. Agar bisa mengerjakan soal dengan baik, pahami dulu beberapa rumus terkait barisan dan deret geometri berikut:

rumus barisan dan deret geometri

Berikut ini diberikan beberapa contoh soal terkait barisan dan deret geometri beserta pembahasannya. Semoga bermanfaat!

Contoh 1:

Diketahui sebuah barisan geometri: 3, 9, 27, 81, 243. Tentukanlah rasio barisan geometri tersebut.

  1. 2
  2. 3
  3. 4
  4. 5
  5. 6
Pembahasan »

Rasio barisan geometri ini adalah 3, yang diperoleh dari:

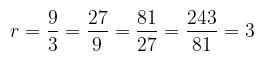
Gambar

Jawaban B.

Contoh 2:

Diketahui sebuah barisan geometri adalah sebagai berikut: 3, 6, 12, 24, 48,..... Tentukanlah suku ketujuh dari barisan geometri ini.

  1. 186
  2. 192
  3. 201
  4. 225
Pembahasan »

Diketahui suku pertama barisan tersebut yaitu a = 3 dan rasionya adalah r = 2. Dengan demikian, suku ketujuh dari barisan geometri tersebut, yaitu:

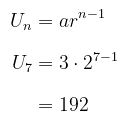
Gambar

Jawaban B.

Contoh 3:

Diketahui suku pertama dari barisan geometri adalah 5/2 dan suku ke-4 adalah 20. Besar suku ke-6 dari barisan tersebut adalah...

  1. 80
  2. 50
  3. 25
  4. -25
  5. -80
Pembahasan »

Diketahui suku pertama deret tersebut yaitu \( U_1 = a = \frac{5}{2}\) dan \( U_4 = 20 \). Untuk menentukan suku ke-6, kita perlu cari rasio barisan tersebut terlebih dahulu, yakni:

Gambar

Dengan demikian, suku ke-6 barisan geometri tersebut adalah:

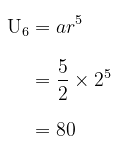
Gambar

Jawaban A.

Contoh 4:

Suatu barisan geometri dengan suku pertama 16 dan \( U_4 = 2 \). Jumlah 6 suku pertama barisan tersebut adalah...

  1. 31
  2. 31,5
  3. 32
  4. 63
  5. 64
Pembahasan »

Diketahui \( U_1 = a = 16 \) dan \( U_4 = 2 \). Kita cari dulu rasio barisan tersebut, yaitu:

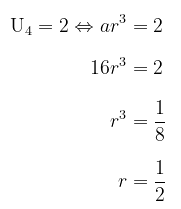
Gambar

Dengan demikian, jumlah 6 suku pertama barisan geometri tersebut adalah:

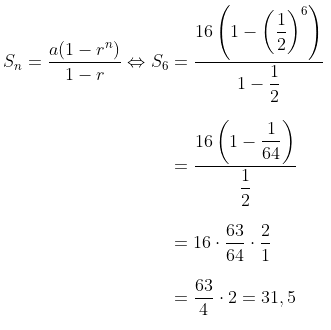
Gambar

Jawaban B.

Contoh 5:

Suku ke-\(n\) deret geometri adalah \( U_n \). Jika diketahui bahwa \( \frac{U_6}{U_8} = 3 \ \text{dan} \ \frac{U_2}{U_8} = \frac{1}{3} \) maka nilai \( U_{10} = \cdots \)

  1. \( 1/27 \)
  2. \( \sqrt{3}/27 \)
  3. \( 1/9 \)
  4. \( \sqrt{3}/9 \)
  5. \( 1/3 \)
Pembahasan »

Diketahui bahwa \( \frac{U_6}{U_8} = 3 \), sehingga kita peroleh:

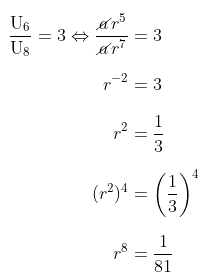
Gambar

Diketahui juga bahwa \( \frac{U_2}{U_8} = \frac{1}{3} \), sehingga kita peroleh:

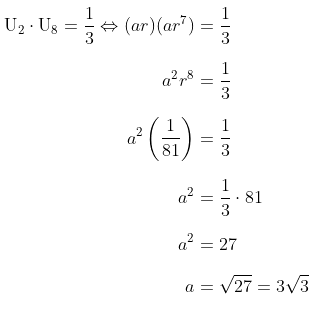
Gambar

Setelah mendapatkan nilai \(a\), sekarang kita perlu mencari nilai \(r\), yakni:

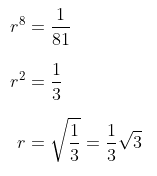
Gambar

Dengan demikian, suku ke-10 barisan tersebut adalah:

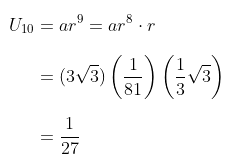
Gambar

Jawaban A.

Contoh 6:

Misalkan \( U_n \) menyatakan suku ke-\(n\) barisan geometri. Jika diketahui \( U_5 = 12 \) dan \( \log \text{U}_4 + \log \text{U}_5-\log \text{U}_6 = \log 3 \) maka nilai \( U_4 \) adalah...

  1. 12
  2. 10
  3. 8
  4. 6
  5. 4
Pembahasan »

Perhatikan bahwa:

Gambar

Dari hasil di atas diperoleh \( U_3 = 3 \) dan \( U_5 = 12 \) sehingga \( U_4 \) yang merupakan nilai tengah antara \( U_3 \) dan \( U_5 \) dapat dicari sebagai berikut:

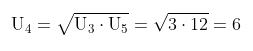
Gambar

Jadi, nilai dari \( U_4 \) adalah 6.

Jawaban D.

Contoh 7:

Jika \((2x-5), \ (x-4), \ (-3x+10)\) merupakan tiga suku pertama barisan geometri, maka nilai \(x\) yang bulat adalah...

  1. 3
  2. 7
  3. 9
  4. 10
  5. 13
Pembahasan »

Dalam barisan geometri berlaku:

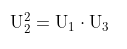
Gambar

Dengan demikian, diperoleh:

Gambar

Karena nilai \(x\) yang diinginkan adalah bilangan bulat, maka nilai \(x\) yang memenuhi adalah 3.

Jawaban A.

Contoh 8: UNBK MTK IPA 2018

Diketahui \( U_n \) menyatakan suku ke-n suatu barisan geometri yang suku-sukunya positif. Jika \( U_7-U_3=24\sqrt{2} \) dan \( U_5 = 3\sqrt{3} U_2 \), suku ke-6 barisan tersebut adalah…

  1. \( \sqrt{2} \)
  2. \( \sqrt{6} \)
  3. \( 3\sqrt{6} \)
  4. \( 9\sqrt{2} \)
  5. \( 9\sqrt{6} \)
Pembahasan »

Ingat bahwa rumus suku ke-n barisan geometri yaitu \( U_n = ar^{n-1} \) sehingga untuk \( U_7-U_3=24\sqrt{2} \) dan \( U_5 = 3\sqrt{3} U_2 \), diperoleh:

\begin{aligned} U_7-U_3 &= 24\sqrt{2} \\[8pt] ar^6-ar^2 &= 24\sqrt{2} \qquad \cdots (1) \\[8pt] U_5 &= 3\sqrt{3}U_2 \\[8pt] ar^4 &= 3\sqrt{3} \ ar \\[8pt] r^3 &= 3\sqrt{3} \Leftrightarrow r^3 = (\sqrt{3})^3 \\[8pt] r &= \sqrt{3} \end{aligned}

Selanjutnya, masukkan \( r = \sqrt{3} \) ke persamaan (1) di atas, diperoleh:

\begin{aligned} ar^6-ar^2 &= 24\sqrt{2} \\[8pt] a(\sqrt{3})^6-a(\sqrt{3})^2 &= 24\sqrt{2} \\[8pt] 27a-3a &= 224\sqrt{2} \\[8pt] 24a &= 24\sqrt{2} \\[8pt] a &= \sqrt{2} \\[8pt] U_n = ar^{n-1} \Leftrightarrow U_6 &= (\sqrt{2})(\sqrt{3})^5 \\[8pt] &= (\sqrt{2})(\sqrt{3})^4 \sqrt{3} \\[8pt] &= 9\sqrt{6} \end{aligned}

Jawaban E.

Contoh 9: UNBK MTK IPA 2019

Seorang peneliti melakukan pengamatan terhadap bakteri tertentu. Setiap ½ hari bakteri membelah diri menjadi dua. Pada awal pengamatan terdapat 2 bakteri. Jika setiap 2 hari ¼ dari jumlah bakteri mati, banyak bakteri setelah 3 hari adalah…

  1. 48 bakteri
  2. 64 bakteri
  3. 96 bakteri
  4. 128 bakteri
  5. 192 bakteri
Pembahasan »

Dari soal diketahui bahwa pada awal pengamatan terdapat 2 bakteri, kemudian ½ hari pertama menjadi 4, 1 hari pertama menjadi 8, 1 ½ hari pertama menjadi 16 dan 2 hari pertama menjadi 32.

Karena setiap 2 hari, ¼ dari jumlah bakteri mati maka jumlah bakteri yang mati yaitu ¼ x 32 = 8. Sehingga bakteri yang tersisa yaitu 24 yang diperoleh dari 32-8=24.

Pada 2 ½ hari pertama jumlah bakteri membelah lagi menjadi 2 sehingga menjadi 48 bakteri dan pada 3 hari pertama menjadi 96 bakteri.

Dengan demikian, banyak bakteri setelah 3 hari yaitu 96 bakteri.

Jawaban C.

Contoh 10: UNBK MTK IPA 2019

Sebuah bola tenis dijatuhkan dari ketinggian 2m dan memantul kembali dengan ketinggian ¾ kali tinggi sebelumnya. Pemantulan ini berlangsung terus menerus hingga bola berhenti. Jumlah seluruh lintasan bola adalah…

  1. 12 m
  2. 14 m
  3. 16 m
  4. 18 m
  5. 20 m
Pembahasan »

Untuk mendapatkan pemahaman yang lebih baik dari soal di atas, perhatikan ilustrasi berikut:

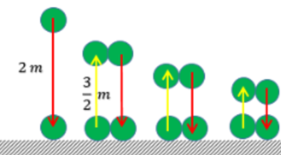
Gambar

Dari gambar di atas terlihat bahwa lintasan bola mengalami turun dan naik. Untuk lintasan turun (warna merah), diperoleh:

\begin{aligned} a &= 2, \ r = \frac{3}{4} \\[8pt] S_\infty &= \frac{a}{1-r} = \frac{2}{1-\frac{3}{4}} \\[8pt] &= \frac{2}{1/4} = 8 \end{aligned}

Dan untuk lintasan naik (warna hijau), diperoleh:

\begin{aligned} a &= 3/2, \ r = \frac{3}{4} \\[8pt] S_\infty &= \frac{3/2}{1-r} = \frac{3/2}{1-\frac{3}{4}} \\[8pt] &= \frac{3/2}{1/4} = 6 \end{aligned}

Jadi, total lintasan bola yaitu 8 + 6 = 14 m.

Jawaban B.

Contoh 11: UNBK MTK IPA 2018

Suku ke-6 dari barisan geometri \( 36+24+16+\cdots \) adalah…

  1. \( 4 \frac{18}{27} \)
  2. \( 4 \frac{20}{27} \)
  3. \( 7 \frac{1}{9} \)
  4. \( 9 \frac{2}{3} \)
  5. \( 10 \frac{2}{3} \)
Pembahasan »

Dari deret di atas diketahui \(a = 36\) dan \( r = \frac{U_2}{U_1} = \frac{24}{36} = \frac{2}{3}\) sehingga suku ke-6 barisan geometri tersebut yaitu:

\begin{aligned} U_n &= ar^{n-1} \\[8pt] U_6 &= 36 \cdot \left( \frac{2}{3} \right)^{6-1} = 36 \cdot \left( \frac{2}{3} \right)^5 \\[8pt] &= 36 \cdot \frac{32}{243} = 4 \cdot \frac{32}{27} \\[8pt] &= \frac{128}{27} = 4 \ \frac{20}{27} \end{aligned}

Jawaban B.

Contoh 12: UNBK MTK IPS 2017

Pertambahan penduduk suatu kota setiap tahun diasumsikan mengikuti barisan geometri. Pada tahun 2011 pertambahannya sebanyak 4 orang dan pada tahun 2013 sebanyak 64 orang. Pertambahan penduduk pada tahun 2015 adalah…

  1. 256 orang
  2. 572 orang
  3. 1.024 orang
  4. 2.048 orang
  5. 3.032 orang
Pembahasan »

Ingat bahwa rumus suku ke-n barisan geometri yaitu \(U_n = ar^{n-1}\). Dari soal diketahui \(a = 4\) dan \(U_3 = 64\) sehingga diperoleh:

\begin{aligned} U_n &= ar^{n-1} \\[8pt] U_3 &= 64 \Leftrightarrow 64 = 4 \cdot r^{3-1} \\[8pt] 64 &= 4r^2 \Leftrightarrow r^2 = 16 \\[8pt] r &= \sqrt{16} = \pm 4 \\[8pt] \text{tahun 2015} = U_5 &= 4 \cdot (\pm 4)^{5-1} \\[8pt] &= 4 \cdot (\pm 4)^4 \\[8pt] &= 1.024 \end{aligned}

Jadi, pertambahan penduduk pada tahun 2015 adalah 1.024.

Jawaban C.

Contoh 13: UNBK MTK IPS 2017

Diketahui barisan geometri dengan suku ke-5 adalah 16 dan suku ke-8 adalah 128. Suku ke-12 barisan tersebut adalah…

  1. 256
  2. 1.024
  3. 2.048
  4. 3.164
  5. 4.096
Pembahasan »

Ingat bahwa rumus suku ke-n barisan geometri yaitu \(U_n = ar^{n-1}\). Dari soal diketahui \(U_5 = 16\) dan \(U_8 = 128 \) sehingga diperoleh:

\begin{aligned} U_5 &= 16 \Leftrightarrow ar^4 = 16 \qquad \cdots(1) \\[8pt] U_8 &= 128 \Leftrightarrow ar^7 = 128 \qquad \cdots(2) \\[8pt] \frac{U_8}{U_5} &= \frac{ar^7}{ar^4} = \frac{128}{16} \\[8pt] r^3 &= 8 \Leftrightarrow r = 2 \\[8pt] ar^4 &= 16 \Leftrightarrow a \cdot 2^4 = 16 \\[8pt] a \cdot 16 &= 16 \Rightarrow a = \frac{16}{16} = 1 \end{aligned}

Dari hasil di atas diperoleh \(a = 1\) dan \(r = 2\) sehingga suku ke-12 barisan tersebut, yaitu:

\begin{aligned} U_{12} &= ar^{12-1} = 1 \cdot 2^{11} \\[8pt] &= 2.048 \end{aligned}

Jawaban C.

Contoh 14: UN MTK IPA 2013

Sebuah mobil dibeli dengan harga Rp60.000.000,00. Setiap tahun nilai jualnya menjadi ¾ dari harga sebelumnya. Nilai jual setelah dipakai 3 tahun adalah…

  1. Rp20.000.000,00
  2. Rp25.312.000,00
  3. Rp33.750.000,00
  4. Rp35.000.000,00
  5. Rp45.000.000,00
Pembahasan »

Harga mobil akhir tahun pertama (H1), yaitu:

\[ H_1 = \frac{3}{4} \times 60.000.000 = Rp45.000.000 \]

Harga mobil akhir tahun kedua (H2), yaitu:

\[ H_2 = \frac{3}{4} \times 45.000.000 = Rp33.750.000 \]

Harga mobil akhir tahun ketiga (H3), yaitu:

\[ H_3 = \frac{3}{4} \times 33.750.000 = Rp25.312.500 \]

Jawaban B.

Contoh 15: UNBK MTK IPA 2017

Suatu barisan geometri \( 16, 8, 4, 2, \cdots \), maka jumlah \(n\) suku pertama adalah…

  1. \( 2^{n-5}-32 \)
  2. \( 2^{5-n}-32 \)
  3. \( 32-2^{5-n} \)
  4. \( 32-2^{n-5} \)
  5. \( 32-\left( \frac{1}{2} \right)^{5-n} \)
Pembahasan »

Dari soal diketahui suku pertama \(a = 16\) dan rasio \(r = \frac{8}{16} = \frac{1}{2}\) sehingga rumus jumlah \(n\) suku pertama barisan geometri tersebut, yaitu:

\begin{aligned} S_n &= \frac{a(1-r^n)}{1-r^n} = \frac{16 \cdot \left(1- \left( \frac{1}{2} \right)^n \right )}{1-\frac{1}{2}} \\[8pt] &= \frac{2^4 \cdot (1-2^{-n})}{\frac{1}{2}} = 2^5(1-2^{-n}) \\[8pt] &= 2^5-2^5 \cdot 2^{-n} \\[8pt] &= 32-2^{5-n} \end{aligned}

Jawaban C.

Contoh 16: UNBK MTK IPA 2016

Seutas tali dipotong-potong menjadi 6 bagian dengan panjang potongan-potongan tersebut membentuk barisan geometri. Jika panjang potongan terpendek 10 cm dan terpanjang 320 cm, panjang tali sebelum dipotong adalah…

  1. 310 cm
  2. 470 cm
  3. 550 cm
  4. 630 cm
  5. 650 cm
Pembahasan »

Berdasarkan informasi pada soal, maka kita peroleh berikut:

\begin{aligned} n &= 6, \ a=U_1 = 10 \\[8pt] U_6 &= ar^5 = 320 \\[8pt] 10 \cdot r^5 &= 320 \\[8pt] r^5 &= \frac{320}{10} = 32 \\[8pt] r &= \sqrt[5]{32} = 2 \end{aligned}

Panjang tali sebelum dipotong sama dengan jumlah 6 potongan tali tersebut, sehingga diperoleh:

\begin{aligned} S_n &= \frac{a(r^n-1)}{r-1} \Leftrightarrow S_6 = \frac{10 \cdot (2^6-1)}{2-1} \\[8pt] S_6 &= \frac{10 \cdot (64-1)}{1} = 10 \cdot 63 \\[8pt] &= 630 \ cm \end{aligned}

Jawaban D.

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.

Artikel Terkait
img

Barisan dan deret aritmetika: Rumus, contoh soal dan pembahasan

img

Barisan dan deret geometri: Rumus, contoh soal dan pembahasan

img

Barisan dan deret tak hingga: Rumus, contoh soal dan pembahasan