www.jagostat.com

www.jagostat.com

Website Belajar Matematika & Statistika

Website Belajar Matematika & Statistika

Matematika Dasar › Barisan dan Deret › Latihan Soal dan Pembahasan Barisan dan Deret Aritmatika
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552

Latihan Soal dan Pembahasan Barisan dan Deret Aritmatika

Salah satu cara agar dapat memahami barisan aritmetika dengan lebih cepat adalah dengan banyak mengerjakan latihan soal. Agar bisa mengerjakan soal dengan baik, pahami dulu beberapa rumus terkait barisan dan deret aritmetika berikut:

rumus barisan dan deret aritmatika

Berikut ini diberikan 10 contoh soal terkait barisan dan deret aritmetika beserta pembahasannya. Semoga bermanfaat!

Contoh 1:

Tentukanlah rumus umum suku ke-\(n\) dari barisan 5, -2, -9, -16, ....

  1. \( U_n = 12-7n \)
  2. \( U_n = 12+7n \)
  3. \( U_n = 7n-12 \)
  4. \( U_n = 7n+12 \)
  5. \( U_n = -7n+12 \)
Pembahasan »

Diketahui \(a = 5\) dan \(b = -7\). Dengan demikian, rumus umum suku ke-\(n\) barisan tersebut adalah:

Gambar

Jadi, rumus suku ke-\(n\) barisan aritmatika tersebut adalah \( U_n = 12-7n \).

Contoh 2:

Diketahui barisan aritmetika dengan suku pertama 3 dan suku ke-5 adalah 11. Suku ke-25 dari barisan tersebut adalah...

  1. 73
  2. 70
  3. 68
  4. 61
  5. 51
Pembahasan »

Kita tahu bahwa rumus suku ke-\(n\) barisan aritmatika adalah \( U_n = a + (n-1)b \). Untuk menentukan suku ke-25 barisan tersebut, maka terlebih dahulu harus ditemukan nilai \(a\) dan \(b\). Dari soal diketahui \(a = 3\). Selanjutnya, cari nilai \(b\), yakni:

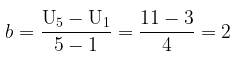
Gambar

Dengan demikian, suku ke-25 barisan tersebut adalah:

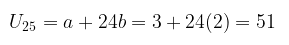
Gambar

Jawaban E.

Contoh 3:

Dari suatu deret aritmatika, diketahui suku pertama adalah 20 dan dan suku keenam adalah 40. Jumlah sepuluh suku pertama dari deret tersebut adalah...

  1. 340
  2. 350
  3. 360
  4. 370
  5. 380
Pembahasan »

Dari soal diketahui \(a = 20\) dan \( U_6 = 40 \). Untuk mencari jumlah sepuluh suku pertama, maka cari nilai \(b\) terlebih dahulu, yakni:

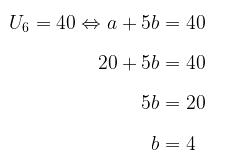
Gambar

Dengan demikian, jumlah sepuluh suku pertama deret tersebut adalah

Gambar

Jawaban E.

Contoh 4:

Dari suatu barisan aritmatika diketahui suku keempat adalah 7 dan jumlah suku keenam dan kedelapan adalah 23. Besar suku ke-20 adalah...

  1. 21
  2. 20
  3. 31
  4. 41
  5. 60
Pembahasan »

Dari soal diketahui bahwa:

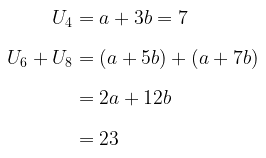
Gambar

Dengan menggunakan metode substitusi diperoleh nilai suku pertama dan beda barisan sebagai berikut:

Gambar

Karena \(b = 3/2\), maka:

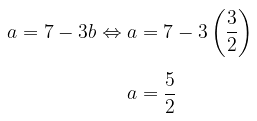
Gambar

Jadi, suku ke-20 barisan aritmatika tersebut adalah:

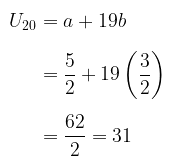
Gambar

Jawaban C.

Contoh 5:

Suku pertama suatu barisan aritmetika adalah 5. Diketahui suku kesepuluh adalah dua kali suku keempat. Jumlah enam suku pertama barisan tersebut adalah...

  1. 55
  2. 58
  3. 61
  4. 64
  5. 67
Pembahasan »

Dari soal diketahui bahwa \( U_1 = a = 5 \) dan karena suku kesepuluh adalah dua kali suku keempat, maka kita peroleh:

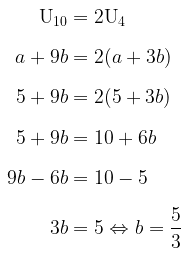
Gambar

Dengan demikian, jumlah enam suku pertama barisan tersebut adalah:

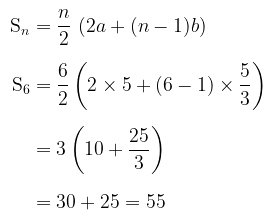
Gambar

Jadi, jumlah enam suku pertama barisan tersebut adalah 55.

Jawaban A.

Contoh 6:

Jumlah 5 suku pertama deret aritmatika adalah 20. Jika masing-masing suku dikurangi dengan suku ke-3, maka hasil kali suku ke-1, ke-2, ke-4, dan ke-5 adalah 324. Jumlah 8 suku pertama deret tersebut adalah....

  1. -4 atau 68
  2. -52 atau 116
  3. -64 atau 88
  4. -44 atau 124
  5. -56 atau 138
Pembahasan »

Diketahui \( S_5 = 20 \) dan karena masing-masing suku dikurangi dengan suku ke-3, maka kita peroleh:

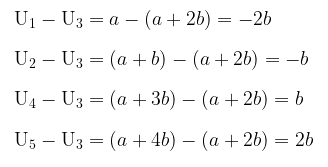
Gambar

Dengan menghitung hasil kali suku-suku baru tersebut, diperoleh:

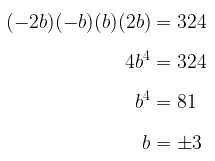
Gambar

Karena \( S_5 = 20 \), maka kita peroleh:

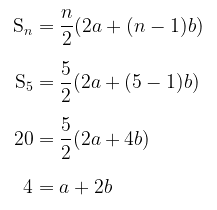
Gambar

Untuk \(b = 3\), maka:

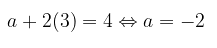
Gambar

Untuk \(b = -3\), maka:

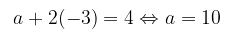
Gambar

Selanjutnya adalah mencari nilai \( S_8 \). Terdapat dua kondisi untuk ini yakni:

Untuk \(a = -2\) dan \(b = 3\), maka:

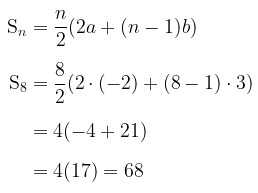
Gambar

Untuk \(a = 10\) dan \(b = -3\), maka:

Gambar

Jadi, jumlah delapan suku pertama deret tersebut adalah -4 dan 68.

Jawaban A.

Contoh 7:

Rumus suku ke-n dari barisan aritmatika \( 5,2,-1,-4, \cdots \) adalah…

  1. \( U_n = 5n-3 \)
  2. \( U_n = 3n+2 \)
  3. \( U_n = 3n-8 \)
  4. \( U_n = -3n-8 \)
  5. \( U_n = -3n+8 \)
Pembahasan »

Dari soal diketahui \(a=6\) dan \(b=4\) sehingga berdasarkan formula suku ke-\(n\) barisan aritmatika, kita peroleh hasil berikut:

\begin{aligned} U_n &= a + (n-1) \cdot b \\[8pt] &= 6 + (n-1) \cdot 4 \\[8pt] &= 6+4n-4 \\[8pt] &= 4n+2 \end{aligned}

Jadi, rumus umum suku ke-\(n\) adalah \( U_n = 4n+2 \).

Jawaban C.

Contoh 8:

Diketahui barisan aritmatika dengan \( U_5 = 17 \) dan \( U_{10} = 32 \). Suku ke-20 adalah…

  1. 57
  2. 62
  3. 67
  4. 72
  5. 77
Pembahasan »

Ingat bahwa rumus untuk suku ke-\(n\) bariasan aritmatika adalah \( U_n = a+(n-1)b \). Untuk menyelesaikan soal ini, pertama kita cari dulu nilai \(b\) dan \(a\). Nilai \(b\) dapat diperoleh dengan rumus sebagai berikut:

\begin{aligned} b &= \frac{U_n-U_m}{n-m} = \frac{U_{10}-U_5}{10-5} \\[8pt] &= \frac{32-17}{10-5} = \frac{15}{5} \\[8pt] &= 3 \end{aligned}

Selanjutnya, akan dicari nilai \(a\) (suku pertama) menggunakan persamaan \( U_5 = 17 \), yakni:

\begin{aligned} U_n &= a + (n-1)b \\[8pt] U_5 &= a + (5-1) \cdot 3 \\[8pt] 17 &= a+12 \\[8pt] a &= 17-12 \\[8pt] &=5 \end{aligned}

Dengan demikian, suku ke-20 barisan tersebut, yaitu:

\begin{aligned} U_n &= a + (n-1)b \\[8pt] U_{20} &= 5 + (20-1) \cdot 3 \\[8pt] &= 5 + 19 \cdot 3 \\[8pt] &= 5+57 \\[8pt] &= 62 \end{aligned}

Jawaban B.

Contoh 9:

Diketahui barisan aritmatika dengan beda positif memiliki suku tengah 17. Apabila jumlah \(n\) suku pertama barisan aritmatika tersebut adalah 221 dan selisih antara suku ke-\(n\) dengan suku pertama adalah 24, maka suku pertama barisan tersebut adalah…

  1. 1
  2. 4
  3. 5
  4. 6
  5. 9
Pembahasan »

Dari soal diketahui selisih antara suku ke-\(n\) dengan suku pertama adalah 24 dan suku tengah barisan aritmatika itu adalah 17, sehingga diperoleh berikut ini:

\begin{aligned} U_n-U_1 &= 24 \Leftrightarrow U_n = U_1 + 24 \\[8pt] \frac{U_1 + U_n}{2} &= 17 \\[8pt] U_1 + (U_1+24) &= 17 \times 2 \\[8pt] 2U_1 + 24 &= 34 \\[8pt] 2U_1 &= 34-24 \\[8pt] U_1 &= \frac{10}{2} = 5 \end{aligned}

Jadi, suku pertama barisan tersebut adalah 5.

Jawaban C.

Contoh 10:

Dalam suatu deret aritmatika, jumlah suku ke-3 dan ke-5 adalah 14, sedangkan jumlah 12 suku pertamanya adalah 129. Jika suku ke-\(n\) adalah 193, nilai \(n = \cdots\)

  1. 118
  2. 122
  3. 126
  4. 128
  5. 130
Pembahasan »

Karena jumlah suku ke-3 dan ke-5 adalah 14, maka kita peroleh:

\begin{aligned} U_3 + U_5 &= 14 \\[8pt] (a+2b)+(a+4b) &= 14 \\[8pt] 2a+6b &= 14 \\[8pt] 2a &= 14-6b \qquad \cdots (1) \end{aligned}

Karena jumlah 12 suku pertamanya adalah 129, kita peroleh:

\begin{aligned} S_n &= \frac{n}{2}(2a+(n-1) \cdot b) \\[8pt] S_{12} &= \frac{12}{2}((14-6b)+(12-1)b) \\[8pt] 129 &= 6(14+5b) \\[8pt] 129 &= 84 + 30b \\[8pt] 30b &= 129-84 \\[8pt] b &= \frac{45}{30} = \frac{3}{2} \end{aligned}

Selanjutnya, substitusi nilai \(b = \frac{3}{2}\) ke persamaan (1) yang diperoleh di atas.

\begin{aligned} 2a &= 14-6b \\[8pt] 2a &= 14-6 \cdot \frac{3}{2} \\[8pt] 2a &= 5 \Rightarrow a = \frac{5}{2} \end{aligned}

Dari soal diketahui bahwa suku ke-\(n\) adalah 193, maka dapat kita tuliskan:

\begin{aligned} U_n &= a+(n-1)b \\[8pt] 193 &= \frac{5}{2}+(n-1) \cdot \frac{3}{2} \\[8pt] 386 &= 5+(n-1) \cdot 3 \\[8pt] 381 &= 3(n-1) \\[8pt] n-1 &= \frac{381}{3} = 127 \\[8pt] n &= 127+1 = 128 \end{aligned}

Jadi, nilai \(n\) adalah 128.

Jawaban D.

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.

Artikel Terkait
img

Barisan dan deret aritmetika: Rumus, contoh soal dan pembahasan

img

Barisan dan deret geometri: Rumus, contoh soal dan pembahasan

img

Barisan dan deret tak hingga: Rumus, contoh soal dan pembahasan

Stop being afraid of what could go wrong and start being positive about what could go right.

Unknown