Latihan Soal Barisan dan Deret Aritmetika dan Jawabannya

Matematika Dasar › Barisan dan Deret › Latihan Soal Barisan dan Deret Aritmetika dan Jawabannya

Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552

Latihan Soal Barisan dan Deret Aritmetika dan Jawabannya

Salah satu cara agar dapat memahami barisan aritmetika dengan lebih cepat adalah dengan banyak mengerjakan latihan soal. Agar bisa mengerjakan soal dengan baik, pahami dulu beberapa rumus terkait barisan dan deret aritmetika berikut:

Berikut ini diberikan 10 contoh soal terkait barisan dan deret aritmetika beserta pembahasannya. Semoga bermanfaat!

Contoh 1:

Dalam suatu gedung pertunjukan disusun kursi dengan baris paling depan terdiri dari 12 kursi, baris kedua berisi 14 kursi, baris ketiga berisi 16 kursi, dan seterusnya. Banyaknya kursi pada baris ke-20 adalah...

28 buah
50 buah
58 buah
60 buah
68 buah

Pembahasan »

Dari soal diketahui bahwa \(a = 12\) dan \(b = 2\). Dengan demikian, banyaknya kursi pada baris ke-20 \( (U_{20}) \) adalah:

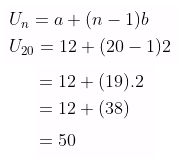
Jawaban C.

Contoh 2:

Misalkan diketahui deret aritmatika yaitu \( 2 + 4 + 6 + \cdots + U_n \). Tentukanlah rumus jumlah \(n\) suku pertama deret bilangan tersebut.

\( U_n = n - n^2 \)
\( U_n = n + n^2 \)
\( U_n = -n + n^2 \)
\( U_n = -n - n^2 \)
\( U_n = 2n + n^2 \)

Pembahasan »

Diketahui suku pertama deret tersebut yaitu \(a = 2\) dan bedanya adalah \(b = 2\). Dengan demikian, rumus jumlah \(n\) suku pertama deret tersebut, yaitu:

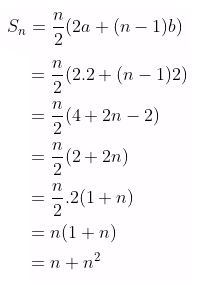
Jawaban B.

Contoh 3:

Diketahui barisan sebagai berikut: \( -1, 1, 3, 5, 7, \cdots \). Tentukanlah rumus umum suku ke-\(n\) untuk barisan tersebut.

\( U_n = n+2 \)
\( U_n = 2n-1 \)
\( U_n = 2n-2 \)
\( U_n = 2n-3 \)
\( U_n = 3n-2 \)

Pembahasan »

Diketahui suku pertama deret tersebut yaitu \(a = -1\) dan bedanya adalah \(b = 2\). Dengan demikian, rumus umum suku ke-\(n\) suku barisan tersebut, yaitu:

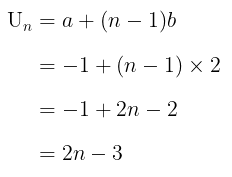
Jawaban D.

Contoh 4:

Diketahui suku ke-5 dan suku ke-9 dari suatu barisan bilangan aritmetika adalah 18 dan 6. Suku ke-3 barisan tersebut adalah⋯⋅

Pembahasan »

Kita tahu bahwa rumus suku ke-n suatu barisan aritmatika ditentukan oleh \( U_n = a + (n-1)b \). Untuk mencari suku ke-3 barisan tersebut, perlu ditentukan nilai \(b\) dan \(a\) terlebih dahulu. Nilai \(b\) dapat ditentukan sebagai berikut:

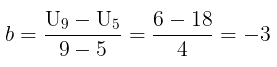
Selanjutnya, nilai \(a\) dapat ditentukan dari salah satu persamaan dari \( U_5 = 18 \) dan \( U_9 = 6 \). Di sini akan digunakan \( U_5 = 18 \).

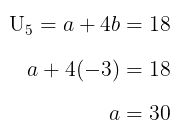
Jadi, suku ke-3 barisan tersebut adalah:

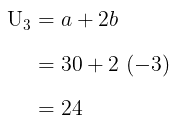
Jawaban E.

Contoh 5:

Diketahui deret aritmatika dengan suku ke-3 adalah 24 dan suku ke-6 adalah 36. Jumlah 15 suku pertama deret tersebut adalah…

Pembahasan »

Dari soal diketahui bahwa \( U_3 = 24 \) dan \( U_6 = 36 \). Ditanya \( S_{15} = ...? \)

Untuk mencari nilai \( S_{15}\), kita perlu menghitung nilai \(a\) dan \(b\) terlebih dahulu. Kita dapat menggunakan metode eliminasi dalam sistem persamaan linear dua variabel.

Untuk \( U_3 = 24 \), kita peroleh:

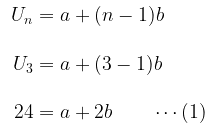
Untuk \( U_6 = 36 \), maka:

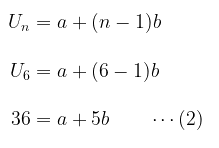
Eliminasi \(a\) dalam persamaan (1) dan (2), yakni:

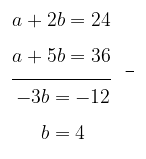
Selanjutnya, substitusi nilai \(b = 4\) ke persamaan 1 (atau ke persamaan 2). Kita peroleh:

Setelah memperoleh nilai \(a\) dan \(b\), sekarang kita bisa menghitung \(S_{15} \), yaitu:

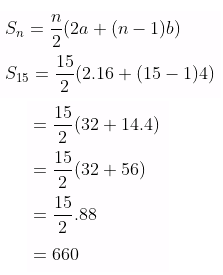
Jawaban B.

Contoh 6:

Diketahui deret sebagai berikut:

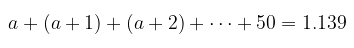
Jika \(a\) adalah bilangan bulat positif, maka nilai \(a = \cdots\)

Pembahasan »

Deret di atas merupakan deret aritmetika karena berselisih 1 dengan suku yang berdekatan. Banyaknya suku deret itu adalah:

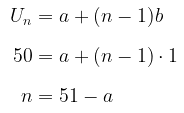
Karena \( S_n = 1.139 \), maka kita peroleh:

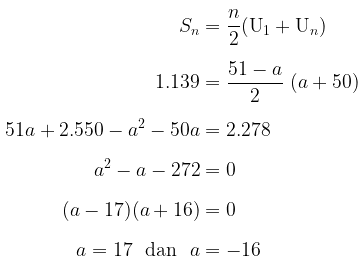
Karena \(a\) adalah bilangan bulat positif, maka dipilih \(a = 17\).

Jawaban C.

Contoh 7:

Rumus suku ke-\(n\) dari barisan aritmatika \( 5,2,-1,-4, \cdots \) adalah…

\( U_n = 5n-3 \)
\( U_n = 3n+2 \)
\( U_n = 3n-8 \)
\( U_n = -3n-8 \)
\( U_n = -3n+8 \)

Pembahasan »

Dari soal diketahui \(a=5\) dan \(b=-3\). Dengan demikian, berdasarkan formula suku ke-\(n\) barisan aritmatika, kita peroleh hasil berikut:

\begin{aligned} U_n &= a + (n-1) \cdot b \\[8pt] &= 5 + (n-1) \cdot (-3) \\[8pt] &= 5-3n+3 \\[8pt] &= -3n+8 \end{aligned}

Jadi, rumus suku ke-\(n\) dari barisan tersebut adalah \( U_n = -3n+8 \).

Jawaban E.

Contoh 8:

Pada barisan aritmatika, nilai suku ke-25 tiga kali nilai suku ke-5. Suku yang bernilai dua kali suku pertama adalah suku ke…

Pembahasan »

Dari soal diketahui \( U_{25} = 3U_5 \) dan berdasarkan rumus suku ke-\(n\) barisan aritmatika yaitu \( U_n = a+(n-1)b \), kita peroleh berikut ini:

\begin{aligned} U_{25} &= 3U_5 \\[8pt] a+24b &= 3(a+4b) \\[8pt] a+24b &= 3a+12b \\[8pt] 2a &= 12b \\[8pt] a &= 6b \end{aligned}

Misalkan suku yang bernilai dua kali suku pertama adalah suku ke-\(n\) sehingga kita tuliskan berikut ini:

\begin{aligned} U_n &= 2U_1 \\[8pt] a+(n-1)b &= 2a \\[8pt] (n-1)b &= a \\[8pt] (n-1)b &= 6b \\[8pt] n-1 &= 6 \Rightarrow n = 7 \end{aligned}

Jadi, suku yang bernilai dua kali suku pertama adalah suku ke-7.

Jawaban D.

Contoh 9:

Diketahui \( \alpha, \beta \), dan \( \gamma \) berturut-turut adalah suku ke-2, suku ke-4, dan suku ke-6 dari suatu barisan aritmatika. Jika \( \displaystyle \frac{\alpha+\beta+\gamma}{\beta+1} = 4 \), maka nilai \(\beta\) adalah…

-4
-1
1
2
4

Pembahasan »

Berdasarkan rumus suku ke-\(n\) barisan aritmatika \( U_n = a+(n-1)b \), kita peroleh:

\begin{aligned} U_2 &= \alpha = a+b \\[8pt] U_4 &= \beta = a+3b \\[8pt] U_6 &= \gamma = a+5b \end{aligned}

Dengan demikian, diperoleh hasil sebagai berikut:

\begin{aligned} \frac{\alpha+\beta+\gamma}{\beta+1} &= 4 \\[8pt] \frac{(a+b)+(a+3b)+(a+5b)}{(a+3b)+1} &= 4 \\[8pt] 3a+9b &= 4a+12b+4 \\[8pt] a+3b &= -4 \\[8pt] U_4 &= \beta = -4 \end{aligned}

Jadi, nilai \(\beta\) adalah -4.

Jawaban A.

Contoh 10:

Jika \(U_n\) menyatakan suku ke-\(n\) suatu barisan aritmatika dan \( U_6-U_8+U_{10}-U_{12}+U_{14} = 20 \), maka jumlah 19 suku pertama barisan tersebut adalah…

Pembahasan »

Pada barisan aritmatika, rumus suku ke-\(n\) dirumuskan oleh \( U_n = a+(n-1)b \). Untuk itu, diperoleh berikut ini:

\begin{aligned} U_6-U_8+U_{10}-U_{12}+U_{14} &= 20 \\[8pt] (a+5b)-(a+7b)+(a+9b)-(a+11b)+(a+13b) &= 20 \\[8pt] a+9b &= 20 \\[8pt] 2a+18b &= 40 \end{aligned}

Jumlah 19 suku pertama barisan aritmatika tersebut dirumuskan sebagai berikut:

\begin{aligned} S_{n} &= \frac{n}{2}(a+U_n) \\[8pt] S_{19} &= \frac{19}{2}(a+U_{19}) = \frac{19}{2}(a+(a+18b)) \\[8pt] &= \frac{19}{2}(2a+18b) = \frac{19}{2} \cdot 40 \\[8pt] &= 380 \end{aligned}

Jadi, jumlah 19 suku pertama barisan aritmatika tersebut adalah 380.

Jawaban B.

Contoh 11: UNBK MTK IPS 2019

Diketahui barisan aritmetika mempunyai suku ke-2 bernilai 4 dan suku ke-8 bernilai 22. Suku ke-15 barisan tersebut adalah…

Pembahasan »

Ingat bahwa rumus suku ke-n barisan aritmetika yaitu \( U_n = a+(n-1)b \) sehingga untuk \( U_2 = 4 \) dan \( U_8 = 22 \), diperoleh:

\begin{aligned} U_n &= a+(n-1)b \\[8pt] U_2 &= 4 \Leftrightarrow a+b = 4 \qquad \cdots(1) \\[8pt] U_8 &= 22 \Leftrightarrow a+7b = 22 \qquad \cdots(2)\end{aligned}

Dengan melakukan eliminasi pada persamaan (1) dan (2), diperoleh:

\begin{aligned} \frac{ \begin{aligned} a+b &= 4 \\[5pt] a+7b &= 22 \\[5pt] \end{aligned} }{ \begin{aligned} \\[-10pt] -6b &= -18 \\[5pt] b &= \frac{-18}{-6} = 3 \end{aligned} } \ - \\[8pt] a = 4-b=4-3=1 \end{aligned}

Dengan demikian, suku ke-15 barisan tersebut, yaitu:

\begin{aligned} U_n &= a+(n-1)b \\[8pt] U_{15} &= 1+(15-1)(3) \\[8pt] &= 1+(14)(3) \\[8pt] &= 43 \end{aligned}

Jawaban A.

Contoh 12: UNBK MTK IPS 2019

Pembahasan »

Ingat bahwa rumus suku ke-n barisan aritmetika yaitu \( U_n = a+(n-1)b \) sehingga untuk \( U_3 = 4 \) dan \( U_{15} = 40 \), diperoleh:

\begin{aligned} U_n &= a+(n-1)b \\[8pt] U_3 &= 4 \Leftrightarrow a+2b = 4 \qquad \cdots(1) \\[8pt] U_{15} &= 40 \Leftrightarrow a+14b = 40 \qquad \cdots(2)\end{aligned}

Dengan melakukan eliminasi pada persamaan (1) dan (2), diperoleh:

\begin{aligned} \frac{ \begin{aligned} a+2b &= 4 \\[5pt] a+14b &= 40 \\[5pt] \end{aligned} }{ \begin{aligned} \\[-10pt] -12b &= -36 \\[5pt] b &= \frac{-36}{-12} = 3 \end{aligned} } \ - \\[8pt] a = 4-2b=-2 \end{aligned}

Dengan demikian, jumlah 20 suku pertama deret tersebut, yaitu:

\begin{aligned} S_n &= \frac{n}{2}(2a+(n-1)b) \\[8pt] S_{20} &= \frac{20}{2}(2(-2)+(20-1)(3)) \\[8pt] &= 10(-4+19(3)) \\[8pt] &= 10(-4+57) \\[8pt] &= 530 \end{aligned}

Jawaban A.

Contoh 13: UNBK MTK IPA 2019

Diketahui suku ke-3 dan ke-7 suatu barisan aritmetika berturut-turut adalah 28 dan 44. Jumlah 25 suku pertama deret tersebut adalah…

1.600
1.650
1.700
1.800
1.850

Pembahasan »

Ingat bahwa rumus suku ke-n barisan aritmetika yaitu \( U_n = a+(n-1)b \) sehingga untuk \( U_3 = 28 \) dan \( U_7 = 44 \), diperoleh:

\begin{aligned} U_n &= a+(n-1)b \\[8pt] U_3 &= 28 \Leftrightarrow a+2b = 28 \qquad \cdots(1) \\[8pt] U_7 &= 44 \Leftrightarrow a+6b = 44 \qquad \cdots(2)\end{aligned}

Dengan melakukan eliminasi pada persamaan (1) dan (2), diperoleh:

\begin{aligned} \frac{ \begin{aligned} a+2b &= 28 \\[5pt] a+6b &= 44 \\[5pt] \end{aligned} }{ \begin{aligned} \\[-10pt] -4b &= -16 \\[5pt] b &= \frac{-16}{-4} = 4 \end{aligned} } \ - \\[8pt] a = 28-2b=20 \end{aligned}

Dengan demikian, jumlah 25 suku pertama deret tersebut, yaitu:

\begin{aligned} S_n &= \frac{n}{2}(2a+(n-1)b) \\[8pt] S_{25} &= \frac{25}{2}(2(20)+(25-1)(4)) \\[8pt] &= \frac{25}{2}(40+24(4)) = \frac{25}{2}(40+96) \\[8pt] &= \frac{25}{2}(136) \\[8pt] &= 1.700 \end{aligned}

Jawaban C.

Contoh 14: UNBK MTK IPS 2018

Seorang ayah menabung uangnya di rumah. Setiap bulan besar tabungan bertambah secara tetap dimulai dari bulan pertama Rp50.000,00, bulan kedua Rp55.000,00, bulan ketiga Rp60.000,00, dan seterusnya. Jumlah tabungan selama 10 bulan adalah…

Rp500.000,00
Rp550.000,00
Rp600.000,00
Rp700.000,00
Rp725.000,00

Pembahasan »

Ingat bahwa rumus jumlah suku ke-n barisan aritmetika yaitu \( S_n = \frac{n}{2}(2a+(n-1)b) \). Dari soal diketahui \(a = 50.000, b = 5.000, \) dan \(n = 10\) sehingga diperoleh:

\begin{aligned} S_n &= \frac{n}{2}(2a+(n-1)b) \\[8pt] S_{10} &= \frac{10}{2}(2(50.000)+(10-1)(5.000)) \\[8pt] &= 5(100.000+9(5.000)) \\[8pt] &= 5(100.000+45.000) \\[8pt] &= 5(145.000) \\[8pt] &= 725.000 \end{aligned}

Jadi, jumlah tabungan selama 10 bulan adalah Rp725.000,00.

Jawaban E.

Contoh 15: UNBK MTK IPS 2017

Suku ke-6 dan ke-10 suatu deret aritmetika berturut-turut adalah 20 dan 32. Jumlah 10 suku pertama deret tersebut adalah…

Pembahasan »

Ingat bahwa rumus suku ke-n barisan aritmetika yaitu \( U_n = a+(n-1)b \) sehingga untuk \( U_6 = 20 \) dan \( U_{10} = 32 \), diperoleh:

\begin{aligned} U_n &= a+(n-1)b \\[8pt] U_6 &= 20 \Leftrightarrow a+5b = 20 \qquad \cdots(1) \\[8pt] U_{10} &= 32 \Leftrightarrow a+9b = 32 \qquad \cdots(2)\end{aligned}

Dengan melakukan eliminasi pada persamaan (1) dan (2), diperoleh:

\begin{aligned} \frac{ \begin{aligned} a+5b &= 20 \\[5pt] a+9b &= 32 \\[5pt] \end{aligned} }{ \begin{aligned} \\[-10pt] -4b &= -12 \\[5pt] b &= \frac{-12}{-4} = 3 \end{aligned} } \ - \\[8pt] a = 20-5b=5 \end{aligned}

Dengan demikian, jumlah 10 suku pertama deret tersebut, yaitu:

\begin{aligned} S_n &= \frac{n}{2}(2a+(n-1)b) \\[8pt] S_{10} &= \frac{10}{2}(2(5)+(10-1)(3)) \\[8pt] &= 5(10+9(3)) \\[8pt] &= 5(10+27) \\[8pt] &= 185 \end{aligned}

Jawaban C.

Contoh 16: UNBK MTK IPA 2017

Adit menabung setiap bulan di sebuah bank. Pada bulan pertama Adit menabung sebesar Rp80.000,00 dan pada bulan berikutnya uang yang ditabung selalu Rp5.000,00 lebih besar dari uang yang ditabung pada bulan sebelumnya. Jumlah uang tabungan Adit selama satu tahun adalah…

Rp1.015.000,00
Rp1.150.000,00
Rp1.290.000,00
Rp1.320.000,00
Rp1.340.000,00

Pembahasan »

Ingat bahwa rumus jumlah suku ke-n barisan aritmetika yaitu \( S_n = \frac{n}{2}(2a+(n-1)b) \). Dari soal diketahui \(a = 80.000, b = 5.000, \) dan \(n = 12\) sehingga diperoleh:

\begin{aligned} S_n &= \frac{n}{2}(2a+(n-1)b) \\[8pt] S_{12} &= \frac{12}{2}(2(80.000)+(12-1)(5.000)) \\[8pt] &= 6(160.000+11(5.000)) \\[8pt] &= 6(160.000+55.000) \\[8pt] &= 6(215.000) \\[8pt] &= 1.290.000 \end{aligned}

Jadi, jumlah tabungan Adit selama satu tahun adalah Rp1.290.000,00.

Jawaban C.

Contoh 17: UNBK MTK IPS 2016

Dalam sebuah barisan aritmetika, suku ke-8 adalah 37 dan suku ke-11 adalah 52. Jumlah sepuluh suku pertama barisan tersebut adalah…

Pembahasan »

Ingat bahwa rumus suku ke-n barisan aritmetika yaitu \( U_n = a+(n-1)b \) sehingga untuk \( U_8 = 37 \) dan \( U_{11} = 52 \), diperoleh:

\begin{aligned} U_n &= a+(n-1)b \\[8pt] U_8 &= 37 \Leftrightarrow a+7b = 37 \qquad \cdots(1) \\[8pt] U_{11} &= 52 \Leftrightarrow a+10b = 52 \qquad \cdots(2)\end{aligned}

Dengan melakukan eliminasi pada persamaan (1) dan (2), diperoleh:

\begin{aligned} \frac{ \begin{aligned} a+7b &= 37 \\[5pt] a+10b &= 52 \\[5pt] \end{aligned} }{ \begin{aligned} \\[-10pt] -3b &= -15 \\[5pt] b &= \frac{-15}{-3} = 5 \end{aligned} } \ - \\[8pt] a = 37-7b=2 \end{aligned}

Dengan demikian, jumlah sepuluh suku pertama deret tersebut, yaitu:

\begin{aligned} S_n &= \frac{n}{2}(2a+(n-1)b) \\[8pt] S_{10} &= \frac{10}{2}(2(2)+(10-1)(5)) \\[8pt] &= 5(4+9(5)) \\[8pt] &= 5(4+45) \\[8pt] &= 245 \end{aligned}

Jawaban A.

Contoh 18: UNBK MTK IPA 2016

Suatu barisan aritmetika memiliki suku kedua adalah 8, suku keempat adalah 14, dan suku terakhir 23. Jumlah semua suku barisan tersebut adalah…

Pembahasan »

Ingat bahwa rumus suku ke-n barisan aritmetika yaitu \( U_n = a+(n-1)b \) sehingga untuk \( U_2 = 8 \) dan \( U_4 = 14 \), diperoleh:

\begin{aligned} U_n &= a+(n-1)b \\[8pt] U_2 &= 8 \Leftrightarrow a+b = 8 \qquad \cdots(1) \\[8pt] U_4 &= 14 \Leftrightarrow a+3b = 14 \qquad \cdots(2)\end{aligned}

Dengan melakukan eliminasi pada persamaan (1) dan (2), diperoleh:

\begin{aligned} \frac{ \begin{aligned} a+b &= 8 \\[5pt] a+3b &= 14 \\[5pt] \end{aligned} }{ \begin{aligned} \\[-10pt] -2b &= -6 \\[5pt] b &= \frac{-6}{-2} = 3 \end{aligned} } \ - \\[8pt] a = 8-b=5 \end{aligned}

Selanjutnya, kita akan cari banyaknya suku barisan aritmetika tersebut, yaitu:

\begin{aligned} U_n &= a+(n-1)b \\[8pt] 23 &= 5+(n-1)(3) \\[8pt] 23 &= 5+3n-3 \\[8pt] 23 &= 3n+2 \\[8pt] n &= \frac{23-2}{3} = 7 \end{aligned}

Dengan demikian, jumlah semua suku barisan tersebut, yaitu:

\begin{aligned} S_n &= \frac{n}{2}(a+Un) \\[8pt] S_7 &= \frac{7}{2}(5+23) = \frac{7}{2}(28) \\[8pt] &= 98 \end{aligned}

Jawaban C.

Contoh 19: UNBK MTK IPA 2013

Suatu pabrik memproduksi barang jenis A pada tahun pertama sebesar 1.960 unit. Tiap tahun produksi turun sebesar 120 unit sampai tahun ke-16. Total seluruh produksi yang dicapai sampai tahun yang ke-16 adalah…

45.760
45.000
16.960
16.000
9.760

Pembahasan »

Ingat bahwa rumus jumlah suku ke-n barisan aritmetika yaitu \( S_n = \frac{n}{2}(2a+(n-1)b) \). Dari soal diketahui \(a = 1.960, b = -120, \) dan \(n = 16\) sehingga diperoleh:

\begin{aligned} S_n &= \frac{n}{2}(2a+(n-1)b) \\[8pt] S_{16} &= \frac{16}{2}(2(1.960)+(16-1)(-120)) \\[8pt] &= 8(3.920+15(-120)) \\[8pt] &= 8(3.920-1.800) \\[8pt] &= 8(2.120) \\[8pt] &= 16.960 \end{aligned}

Jadi, total seluruh produksi yang dicapai sampai tahun yang ke-16 adalah 16.960 unit.

Jawaban C.

Contoh 20: Tryout UNBK MTK IPS 2019

Diketahui barisan aritmetika dengan \(U_n\) adalah suku ke-n. Jika \( U_3+U_{10}+U_{32}=135 \), maka \( U_{15} = \cdots \)

Pembahasan »

Ingat bahwa rumus suku ke-n barisan aritmetika yaitu \( U_n = a+(n-1)b \) sehingga diperoleh:

\begin{aligned} U_3+U_{10}+U_{32} &= 135 \\[8pt] (a+2b)+(a+9b)+(a+31b) &= 135 \\[8pt] 3a+42b &= 135 \\[8pt] 3(a+14b) &= 135 \\[8pt] a+14b &= 45 \\[8pt] U_{15} &= 45 \end{aligned}

Jawaban D.

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.

www.jagostat.com

www.jagostat.com

Website Belajar Matematika & Statistika

Website Belajar Matematika & Statistika

Matematika Dasar › Barisan dan Deret › Latihan Soal Barisan dan Deret Aritmetika dan Jawabannya