www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Kalkulus I » Fungsi › Fungsi Genap dan Fungsi Ganjil
Fungsi Genap dan Fungsi Ganjil
Misalkan diketahui sebuah fungsi \(f(x)\). Jika \(f(-x) = f(x)\) maka grafik tersebut simetri terhadap sumbu-\(y\). Fungsi yang demikian disebut fungsi genap. Sebaliknya, jika \(f(-x)=-f(x)\), maka grafik tersebut simetri terhadap titik asal (0,0). Fungsi yang demikian disebut fungsi ganjil.
Kita telah belajar banyak mengenai grafik fungsi, katakanlah fungsi itu dinotasikan dengan \(f(x)\). Beberapa dari grafik fungsi \(f(x)\) ada yang simetri terhadap sumbu-\(y\) dan ada pula yang simetri terhadap titik asal (0,0). Untuk mengetahui kesimetrisan fungsi ini, kita perlu mengetahui grafik fungsi \(f(x)\) tersebut.
Akan tetapi, tahukah Anda bahwa kesimetrisan suatu fungsi juga dapat ditentukan dengan hanya melihat persamaan atau rumus fungsi tersebut? Kita akan mempelajarinya di tulisan ini.
Fungsi Genap
Katakanlah kita memiliki sebuah fungsi \(f(x)\). Jika
\[ f(-x)=f(x) \]
maka kita katakan grafik tersebut simetri terhadap sumbu-\(y\). Fungsi yang demikian disebut fungsi genap.
Contoh 1:
Fungsi \(f(x)=x^2-x\) di mana grafiknya terlihat dalam Gambar 1 adalah fungsi genap. Ini karena
\begin{aligned} f(-x) &= (-x)^2-(-x) \\[5pt] &= x^2-x \\[5pt] &= f(x) \end{aligned}
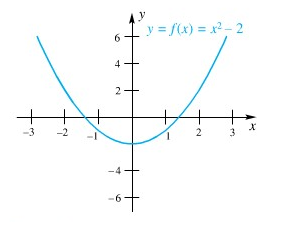
Gambar 1. Grafik fungsi \(f(x)=x^2-x\)
Perhatikan bahwa grafik fungsi \(f(x)\) pada Gambar 1 di atas adalah simetris terhadap sumbu-\(y\) karena fungsi \(f(x)\) termasuk fungsi genap.
Contoh 2:
Fungsi \(f(x)=|2x|\) termasuk fungsi genap, karena
\begin{aligned} f(-x) &= |-2x| \\[5pt] &= |2x| \\[5pt] &= f(x) \end{aligned}
Grafik diperlihatkan pada Gambar 2 berikut.
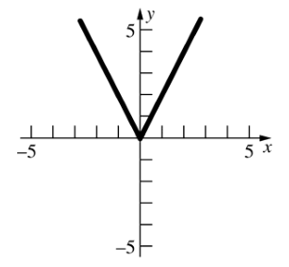
Gambar 2. Grafik fungsi \(f(x)=|2x|\)
Perhatikan bahwa grafik fungsi \(f(x)\) pada Gambar 2 di atas adalah simetris terhadap sumbu-\(y\) karena fungsi \(f(x)\) termasuk fungsi genap.
Fungsi Ganjil
Katakanlah kita memiliki sebuah fungsi \(f(x)\). Jika
\[ f(-x)=-f(x) \]
maka kita katakan grafik tersebut simetri terhadap titik asal (0,0). Fungsi yang demikian disebut fungsi ganjil.
Contoh 3:
Fungsi \(g(x)=x^3-2x\) dengan grafiknya diperlihatkan pada Gambar 3 adalah fungsi ganjil. Ini karena \( g(-x)=-g(x) \), yakni
\begin{aligned} g(-x) &= (-x)^3 - 2(-x) \\[5pt] &= -x^3+2x \\[5pt] &= -(x^3-2x) \\[5pt] &= -g(x) \end{aligned}
Perhatikan bahwa grafik fungsi \(g(x)\) pada Gambar 3 di bawah adalah simetris terhadap titik asal (0,0) karena fungsi \(g(x)\) termasuk fungsi ganjil.

Gambar 3. Grafik fungsi \(g(x)=x^3-2x\)
Contoh 4:
Apakah fungsi \(f(x)\) berikut
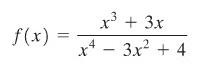
termasuk fungsi genap atau ganjil?
Penyelesaian:
Karena \(f(-x)=-f(x)\), yakni

maka \(f(x)\) termasuk fungsi ganjil. Grafik \(y = f(x)\) yang diperlihatkan dalam Gambar 4 adalah simetris terhadap titik asal.
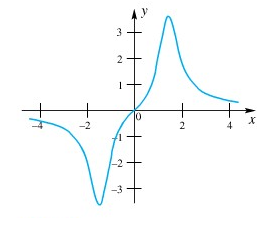
Gambar 4.
Tidak Semua Fungsi Termasuk Fungsi Genap atau Fungsi Ganjil
Sekarang timbul pertanyaan: Apakah semua fungsi dapat dikategorikan sebagai fungsi genap atau fungsi ganji? Jawabannya adalah tidak.
Ambillah contoh fungsi \(h(x)=2/(x-1)\), yang mana grafiknya ditunjukkan dalam Gambar 5. Fungsi ini tidak genap ataupun ganjil. Mengapa? Ini karena \(h(-x)=2/(-x-1)\), yang mana tidak sama dengan \(h(x)\) maupun \(–h(x)\).

Gambar 5. Grafik fungsi \(h(x)=2/(x-1)\)
Perhatikan pula bahwa grafiknya tidak simetri terhadap sumbu \(x\) maupun titik asal. Grafik dari \(h\) adalah simetri terhadap titik \((1,0)\), hasil yang berasal dari kenyataan bahwa \(h(1+x)=-h(1-x)\).
Sifat-sifat Fungsi Genap dan Fungsi Ganjil
Fungsi genap dan fungsi ganjil memiliki beberapa sifat, yaitu:
- Jumlah dua fungsi genap menghasilkan suatu fungsi genap
- Jumlah dua fungsi ganjil menghasilkan suatu fungsi ganjil
- Jumlah fungsi genap dan fungsi ganjil tidak menghasilkan suatu fungsi genap atau fungsi ganjil, kecuali salah satu fungsinya adalah nol.
- Hasilkali dua fungsi genap menghasilkan suatu fungsi genap
- Hasilkali dua fungsi ganjil menghasilkan suatu fungsi genap
- Hasilkali sebuah fungsi genap dengan sebuah fungsi ganjil menghasilkan suatu fungsi ganjil.
Cukup sekian ulasan singkat mengenai fungsi genap dan fungsi ganjil dalam artikel ini. Terima kasih telah membaca artikel ini sampai selesai. Jika Anda merasa artikel ini bermanfaat, boleh dibantu share ke teman-temannya, supaya mereka juga bisa belajar dari artikel ini.
Sumber:
Purcell, Edwin J., dan Dale Verberg. (1987). Calculus with Analytic Geometry, ed 5. Terjemahan Susila, I Nyoman, dkk. Kalkulus dan Geometri Analitis. Indonesia: Penerbit Erlangga.
Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Jangan menyerah. Hal-hal besar membutuhkan waktu. Bersabarlah.
