
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Bahas Soal Matematika » Persamaan › Contoh Soal dan Pembahasan Persamaan Trigonometri Matematika SMA
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552
Contoh Soal dan Pembahasan Persamaan Trigonometri Matematika SMA
Persamaan trigonometri adalah persamaan matematika yang melibatkan perbandingan trigonometri seperti sinus, cosinus, tangen dan sebagainya. Berikut adalah beberapa contoh persaman trigonometri:
\begin{aligned} \sin^2 2x + 4 \sin 2x - 5 &= 0 \\[8pt] \cos(x-15^\circ) &= \frac{1}{2} \sqrt{3} \\[8pt] \sin x &= \frac{1}{2} \\[8pt] \cos x &= \frac{1}{2} \sqrt{3} \end{aligned}
Kebanyakan soal mengenai persamaan trigonometri dirancang untuk mencari penyelesaian dari persamaan tersebut. Penyelesaian persamaan trigonometri yaitu mencari seluruh nilai-nilai sudut \(x\) sehingga persamaan tersebut bernilai benar untuk daerah asal tertentu.
Ada tiga macam bentuk dasar persamaan trigonometri yang dapat dipakai dalam menyelesaikan suatu persamaan trigonometri, antara lain:
1. \( \sin x = \sin \alpha \)
Nilai \(x\) yang memenuhi persamaan ini, yaitu:
\begin{aligned} x &= \alpha + k \cdot 360^\circ \\[8pt] x &= (180^\circ-\alpha) + k \cdot 360^\circ \end{aligned}
Keterangan: \( k \) adalah bilangan bulat.
2. \(\cos x = \cos \alpha \)
Nilai \(x\) yang memenuhi persamaan ini, yaitu:
\begin{aligned} x &= \alpha + k \cdot 360^\circ \\[8pt] x &= -\alpha + k \cdot 360^\circ \end{aligned}
Keterangan: \( k \) adalah bilangan bulat.
3. \(\tan x = \tan \alpha \)
Nilai \(x\) yang memenuhi persamaan ini, yaitu: \( x = \alpha + k \cdot 180^\circ \) di mana \( k \) adalah bilangan bulat.
Satuan yang digunakan dalam persamaan trigonometri bisa berupa derajat atau radian. Ingat bahwa \( 180^\circ = \pi \) radian dan \( 360^\circ = 2\pi \) radian. Pastikan kamu sudah memahami bagaimana cara mengonversi derajat menjadi radian dan begitu juga sebaliknya agar dapat mengerjakan atau menyelesaikan persamaan trigonometri dengan lancar.
Selain penjelasan di atas, kamu mungkin juga perlu mengingat-ingat kembali sudut istimewa trigonometri, karena kita akan sering menggunakannya untuk menyelesaikan soal. Berikut ini diberikan tabel sudut istimewa trigonometri dalam derajat dan radian.

Contoh 1:
Untuk \( 0^\circ \leq x \leq 360^\circ \), himpunan penyelesaian dari \( \sin x = \frac{1}{2} \) adalah…
- \( HP = \{ 30^\circ, 150^\circ \} \)
- \( HP = \{ 30^\circ, 390^\circ \} \)
- \( HP = \{ 30^\circ, 480^\circ \} \)
- \( HP = \{ 120^\circ, 480^\circ \} \)
- \( HP = \{ 390^\circ, 480^\circ \} \)
Pembahasan:
Ubah persamaan dalam soal ke salah satu bentuk dasar persamaan trigonometri, kemudian selesaikan persamaan tersebut sesuai ketentuan yang ada. Perhatikan berikut ini:

Dari persamaan yang diperoleh di atas, kita pilih \(k\) bilangan bulat untuk memperoleh nilai \(x\) yang memenuhi syarat.
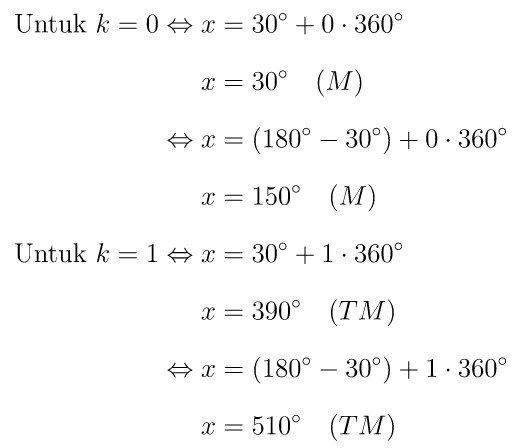
Catatan: Memenuhi (M), Tidak Memenuhi (TM)
Jawaban A.
Baca juga:
Contoh 2:
Tentukan himpunan penyelesaian dari \( \cos x = \frac{1}{2} \) untuk \( 0^\circ \leq x \leq 360^\circ \).
- \( HP = \{ 60^\circ, 420^\circ \} \)
- \( HP = \{ 60^\circ, 300^\circ \} \)
- \( HP = \{ 30^\circ, 360^\circ \} \)
- \( HP = \{ 30^\circ, 120^\circ \} \)
- \( HP = \{ -60^\circ, 120^\circ \} \)
Pembahasan:
Ubah persamaan dalam soal ke salah satu bentuk dasar persamaan trigonometri, kemudian selesaikan persamaan tersebut sesuai ketentuan yang ada. Perhatikan berikut ini:
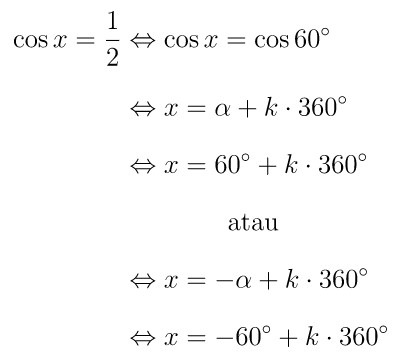
Dari persamaan yang diperoleh di atas, kita pilih \(k\) bilangan bulat untuk memperoleh nilai \(x\) yang memenuhi syarat.
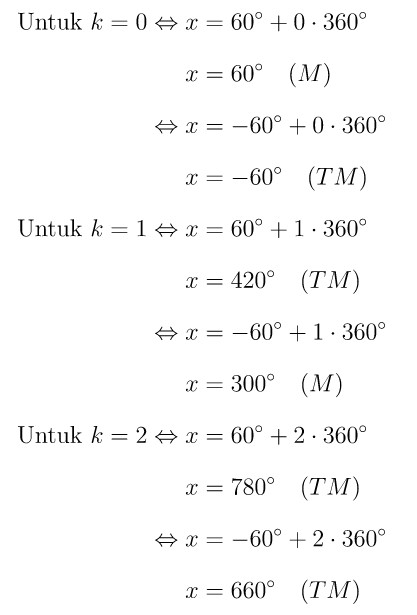
Catatan: Memenuhi (M), Tidak Memenuhi (TM)
Jawaban B.
Contoh 3:
Jika \( \sin(x-600)^\circ = \cos(x-450)^\circ \), maka nilai dari \( \tan x \) adalah…
- \( \sqrt{3} \)
- \( \frac{1}{3}\sqrt{3} \)
- \( 3\sqrt{3} \)
- \( -\sqrt{3} \)
- \( 2\sqrt{3} \)
Pembahasan:
Untuk mencari nilai \(\tan x\), kita perlu mendapatkan nilai \(x\) terlebih dahulu. Ingat bahwa \( \cos x = \sin(90-x) \), di mana dalam hal ini sama dengan \( \cos(x-450)=\sin(90-(x-450)) \). Kita peroleh berikut ini:
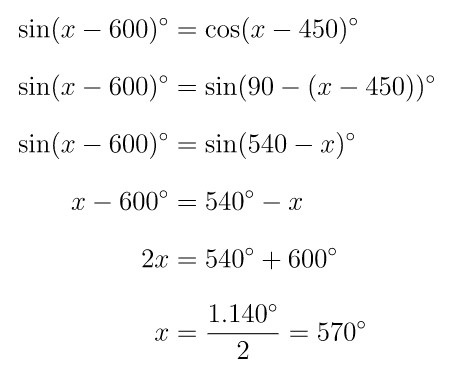
Dengan demikian,
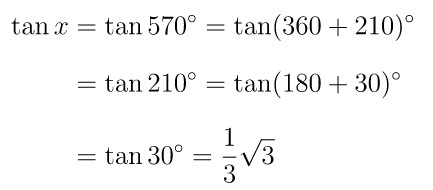
Jawaban B.
Contoh 4:
Himpunan penyelesaian dari \( \cos(x-15^\circ) = \frac{1}{2} \sqrt{3} \) untuk \( 0^\circ \leq x \leq 360 \) adalah…
- \( HP = \{ 45^\circ, 315^\circ \} \)
- \( HP = \{ 45^\circ, 295^\circ \} \)
- \( HP = \{ 45^\circ, 345^\circ \} \)
- \( HP = \{ 75^\circ, 345^\circ \} \)
- \( HP = \{ 75^\circ, 315^\circ \} \)
Pembahasan:
Ubah persamaan dalam soal ke salah satu bentuk dasar persamaan trigonometri, kemudian selesaikan persamaan tersebut sesuai ketentuan yang ada. Perhatikan berikut ini:
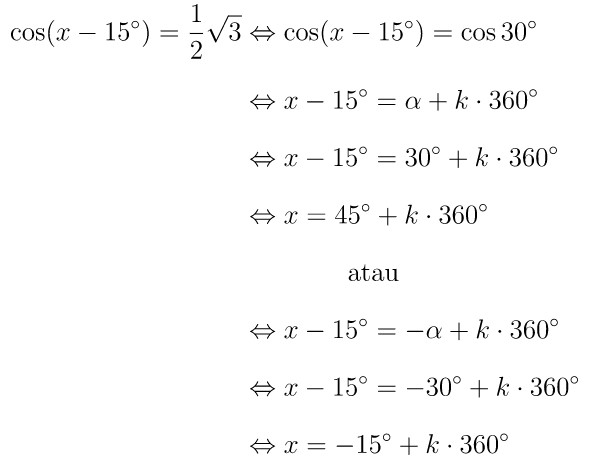
Dari persamaan yang diperoleh di atas, kita pilih \(k\) bilangan bulat untuk memperoleh nilai \(x\) yang memenuhi syarat.

Catatan: Memenuhi (M), Tidak Memenuhi (TM)
Jawaban C.
Baca juga:
Contoh 5:
Himpunan penyelesaian dari \( \tan x = -\sqrt{3} \) untuk \( 0 \leq x \leq 2 \pi \) adalah…
- \( HP = \{ \frac{1}{3}\pi, \frac{2}{3}\pi \} \)
- \( HP = \{ \frac{1}{3}\pi, \frac{5}{3}\pi \} \)
- \( HP = \{ \frac{2}{3}\pi, \frac{5}{3}\pi \} \)
- \( HP = \{ \frac{2}{3}\pi, \frac{4}{3}\pi \} \)
- \( HP = \{ \frac{4}{3}\pi, \frac{5}{3}\pi \} \)
Pembahasan:
Ubah persamaan dalam soal ke salah satu bentuk dasar persamaan trigonometri, kemudian selesaikan persamaan tersebut sesuai ketentuan yang ada. Perhatikan berikut ini:

Dari persamaan yang diperoleh di atas, kita pilih \(k\) bilangan bulat untuk memperoleh nilai \(x\) yang memenuhi syarat.

Catatan: Memenuhi (M), Tidak Memenuhi (TM)
Jawaban C.
Contoh 6:
Himpunan penyelesaian dari \( \sin^2 2x + 4 \sin 2x -5 = 0 \) untuk \( 0^\circ \leq x \leq 360^\circ \) adalah…
- \( HP = \{ 45^\circ, 225^\circ \} \)
- \( HP = \{ 45^\circ, 135^\circ \} \)
- \( HP = \{ 45^\circ, 345^\circ \} \)
- \( HP = \{ 125^\circ, 225^\circ \} \)
- \( HP = \{ 135^\circ, 315^\circ \} \)
Pembahasan:
Untuk menyelesaikan persamaan trigonometri ini, kita misalkan \( p = \sin 2x \). Kita peroleh:

Perhatikan bahwa untuk \( p = -5 \Leftrightarrow \sin 2x = -5 \) tidak memenuhi syarat karena \( -1 \leq \sin x \leq 1 \). Untuk \( p=1 \), diperoleh:

Dari persamaan yang diperoleh di atas, kita pilih \(k\) bilangan bulat untuk memperoleh nilai \(x\) yang memenuhi syarat.
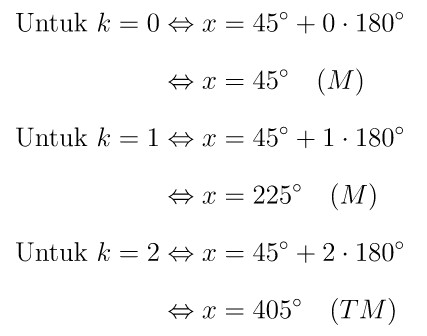
Catatan: Memenuhi (M), Tidak Memenuhi (TM)
Jadi, himpunan penyelesaian dari \( \sin^2 2x + 4 \sin 2x -5 = 0 \) untuk \( 0^\circ \leq x \leq 360^\circ \) adalah \( \{ 45^\circ, 225^\circ \} \).
Jawaban A.
Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan jika ada yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel terkait
You don’t learn to walk by following rules. You learn by doing, and by falling over.
