www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Statistika › Ukuran Pemusatan Data: Rata-rata atau Mean
Ukuran Pemusatan Data: Rata-rata atau Mean
Secara umum, rata-rata dari sekumpulan data adalah jumlah seluruh nilai pada data dibagi dengan banyaknya nilai yang ada.
Rata-rata merupakan salah satu dari ukuran pemusatan data (measure of central tendency) yang sering dan banyak dipakai karena memberikan gambaran yang jelas dan singkat terhadap suatu kumpulan data.
Secara umum, rata-rata dari sekumpulan data adalah jumlah seluruh nilai-nilai pada data dibagi dengan banyaknya nilai yang ada. Rumus untuk menghitung rata-rata dapat dibedakan menjadi rumus rata-rata untuk data tunggal (tidak berkelompok) dan rumus rata-rata untuk data berkelompok.
Rata-rata untuk Data Tunggal (Tidak Berkelompok)
Rata-rata untuk data tidak berkelompok ditentukan dengan rumus:

Perhatikan contoh berikut:
Contoh 1:
Nilai 10 orang peserta ujian matematika dari sebuah SMA adalah 78, 56, 66, 94, 48, 82, 80, 70, 76, dan 50. Tentukan rata-rata dari nilai-nilai tersebut!
Pembahasan:
Dengan menggunakan rumus rata-rata, diperoleh

Rata-rata untuk Data yang Diboboti (Weighted mean)
Misalkan \(x_1, x_2,…,x_n\) adalah \(n\) buah nilai, dengan masing-masing nilai diberi bobot \(f_1,f_2,…,f_n\). Rata-ratanya ditentukan dengan rumus:
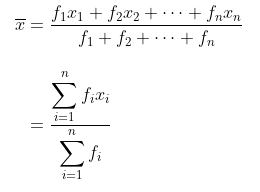
Perhatikan contoh soal berikut:
Contoh 2:
Dalam suatu pekan olahraga nasional, tim suatu provinsi memperoleh 9 medali emas, 7 medali perak, dan 20 perak perunggu. Jika tiap medali emas bernilai 3, medali perak bernilai 2, dan medali perunggu bernilai 1, tentukan nilai rata-rata dari tim provinsi itu!
Pembahasan:
Misalkan bahwa

Dengan demikian,

Jadi, nilai rata-rata provinsi tersebut adalah 10,17.
Contoh 3:
Tentukanlah rata-rata dari data pada Tabel 1 berikut.
Tabel 1. Frekuensi data

Pembahasan:
Langkah-langkah penyelesaiannya adalah sebagai berikut (Lihat Tabel 2):
- Nyatakan nilai-nilai data ke dalam notasi \( x_i \) dan \( f_i \) untuk \( i = 1,2,...,n \)
- Tabel ditambahkan dengan sebuah kolom yang menyatakan hasil kali antara frekuensi \( (f_i) \) dan nilai data \( (x_i) \)
- Tentukan jumlah frekuensi dan jumlah hasil kali antara \( (f_i) \) dan \( (x_i) \)
- Tentukan rata-rata \( (\overline{x}) \)

Tabel 2. Nilai data dan hasil kali frekuensi
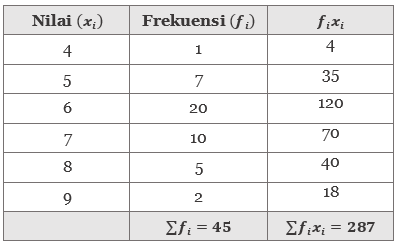
Jadi, rata-ratanya adalah 6,4.
Rata-rata untuk Data Berkelompok
Untuk data yang telah dikelompokkan ke dalam kelas-kelas interval, rata-ratanya dapat ditentukan dengan rumus:
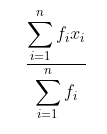
di mana: \( (x_i) \) = titik tengah kelas ke-i
Perhatikan contoh soal berikut:
Contoh 4:
Tentukan rata-rata dari data pada Tabel 3 berikut:
Tabel 3. Frekuensi data

Pembahasan:
Langkah-langkah penyelesaiannya adalah sebagai berikut:
- Tentukan titik tengah kelas \( x_i \) untuk \( i = 1,2,...,n \)
- Hasil kali antara frekuensi \( (f_i) \) dengan titik tengah \( (x_i) \) dimasukkan ke dalam tabel. Tentukan juga hasil kali antara \( f_i \) dan \( x_i \).
- Tentukan rata-ratanya \( (\overline{x}) \)
Dari soal, banyaknya kelas interval adalah 6. Titik tengah kelas \( x_i \) adalah
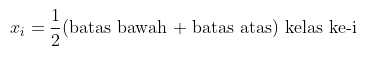
Jadi,
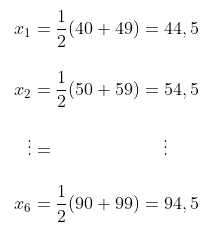

Tabel 2. Frekuensi dan Nilai Tengah


Jadi, rata-ratanya adalah 65,83.
Menghitung Rata-rata dengan Menggunakan Rata-rata Sementara
Kesulitan dalam menghitung rata-rata adalah apabila dijumpai bilangan yang besar atau tidak bulat. Untuk mengatasi hal ini, coba Anda sederhanakan data, yaitu dengan cara memperkirakan nilai rata-rata yang disebut rata-rata sementara. Caranya adalah sebagai berikut.
- Tetapkan rata-rata sementara \((\overline{x}_0)\), dipilih pada kelas yang mempunyai frekuensi tertinggi dan letaknya di tengah.
- Tentukan simpangan (deviasi) terhadap rata-rata sementara, dengan rumus:
- Tentukan rata-rata sesungguhnya, dengan rumus:
- Atau, jika dengan memfaktorkan interval kelasnya maka rumusnya menjadi:



Keterangan:
\( u = \frac{d}{I} = \) faktor interval
\( I = \) lebar kelas atau panjang kelas (interval kelas)
Perhatikan contoh soal berikut:
Contoh 5:
Tentukan rata-rata dari data pada Tabel berikut.
Tabel 2. Frekuensi tinggi

Pembahasan:
Langkah-langkah penyelesaiannya adalah sebagai berikut:
- Tabel 7.8 dilengkapi dengan nilai yang diperlukan sehingga menjadi Tabel 7.9
- Tentukan nilai rata-rata \( (\overline{x}) \)
Tabel 2. Frekuensi, titik tengah, simpangan, dan interval


Cara lain:

Jadi, rata-rata dari data tersebut adalah 164,75.
Cukup sekian penjelasan mengenai ukuran pemusatan data khususnya terkait rata-rata atau mean dalam artikel ini. Semoga bermanfaat.
Sumber:
Sunardi, Slamet Waluyo & Sutrisna. 2014. Konsep dan Penerapan Matematika SMA/MA Kelas XI. Jakarta: Penerbit PT Bumi Aksara.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Twenty years from now you will be more disappointed by the things that you didn’t do than by the ones you did do.
