www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Statistika › Ukuran Pemusatan Data: Nilai Tengah atau Median
Ukuran Pemusatan Data: Nilai Tengah atau Median
Median adalah nilai yang terletak di tengah deretan data setelah diurutkan dari yang terkecil hingga terbesar, atau sebaliknya.
Kita definisikan median atau nilai tengah sebagai angka atau nilai yang memisahkan data yang telah diurutkan menjadi dua bagian yang sama banyak di mana separuh data mempunyai nilai di atas median, sedangkan separuh data lainnya berada di bawah nilai median.
Dengan demikian, kita dapat menghitung median dari suatu kumpulan data dengan mengurutkan semua pengamatan dari nilai terendah ke nilai tertinggi dan kemudian memilih nilai yang berada di tengah.
Perhatikan contoh soal berikut!
Contoh 1:
Tentukanlah median dari data: 6, 3, 4, 2, 5, 7, 6, 5, 3, 5, 2.
Pembahasan:
Data diurutkan lebih dahulu, yaitu: 2, 2, 3, 3, 4, 5, 5, 5, 6, 6, 7.
Jadi, mediannya adalah 5.
Apabila banyaknya data besar, setelah data itu diurutkan maka untuk menentukan mediannya digunakan formula:
Median (Md) = data urutan ke-\( \frac{1}{2} (n+1) \)
Jika setelah menentukan urutan tempat median, ternyata nomor urutan tersebut bukan bilangan cacah maka harus digunakan interpolasi. Perhatikan contoh soal berikut.
Contoh 2:
Tentukan median dari data pada Tabel berikut:
Tabel 1. Frekuensi data
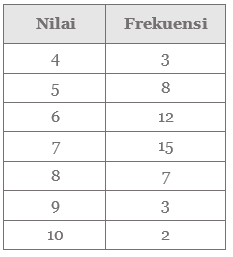
Pembahasan:
Langkah-langkah penyelesaiannya adalah sebagai berikut:
- Tabel 1 dilengkapi dengan nilai yang diperlukan sehingga menjadi seperti pada Tabel 2.
- Tentukan letak median yaitu pada data urutan ke-
Tabel 2. Frekuensi dan frekuensi kumulatif
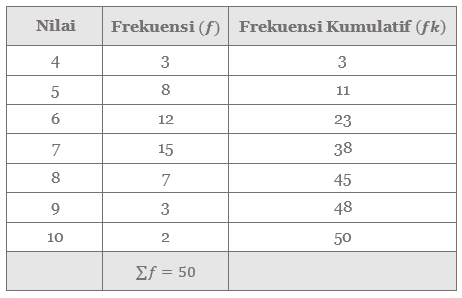

Karena 25,5 bukan bilangan cacah maka digunakan interpolasi. Jadi, mediannya adalah

Ingat bahwa \( Y_{25} \) adalah data ke-25 dan \( Y_{26} \) adalah data ke-26 yaitu 7.
Median untuk Data Berkelompok
Untuk data yang disajikan dalam tabel berkelompok distribusi frekuensi, median dapat dicari dengan rumus:

Keterangan:
\(Tb\) = tepi bawah kelas yang memuat median
\(n\) = jumlah seluruh frekuensi
\(fk\) = frekuensi kumulatif kurang dari di bawah kelas yang memuat median
\(f\) = frekuensi kelas median
\(I\) = lebar atau panjang kelas (interval kelas)
Contoh 3:
Tentukanlah median dari data pada Tabel 3 berikut.
Tabel 3. Frekuensi tinggi

Pembahasan:
Langkah-langkah penyelesaiannya adalah sebagai berikut:
- Tabel 3 dilengkapi dengan nilai yang diperlukan sehingga menjadi seperti Tabel 4.
- Tentukan kelas yang memuat median, yaitu dengan menghitung nilai
Tabel 4. Frekuensi dan frekuensi kumulatif tinggi
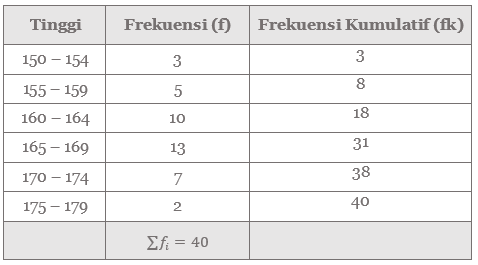

Berarti, kelas median terletak pada kelas 165-169.


Jadi, mediannya adalah 165,27.
Sumber:
Sunardi, Slamet Waluyo & Sutrisna. 2014. Konsep dan Penerapan Matematika SMA/MA Kelas XI. Jakarta: Penerbit PT Bumi Aksara.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Seseorang yang pernah melakukan kesalahan dan tidak pernah memperbaikinya berarti Ia telah melakukan satu kesalahan lagi.
