www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Lingkaran › Persamaan Garis Singgung Lingkaran yang Melalui Suatu Titik pada Lingkaran
Persamaan Garis Singgung Lingkaran yang Melalui Suatu Titik pada Lingkaran
Terdapat tiga kondisi untuk persamaan garis singgung yang melalui titik pada lingkaran, yakni persamaan garis singgung yang melalui suatu titik pada lingkaran yang berpusat di O(0,0), persamaan garis singgung yang melalui suatu titik pada lingkaran yang berpusat di M(a,b), dan persamaan garis singgung yang melalui suatu titik dengan persamaan umum lingkaran.
Pada bagian ini akan dibahas persamaan garis singgung yang melalui suatu titik pada lingkaran. Terdapat tiga kondisi untuk ini, yakni persamaan garis singgung yang melalui suatu titik pada lingkaran yang berpusat di O(0,0), persamaan garis singgung yang melalui suatu titik pada lingkaran yang berpusat di M(a,b), dan terakhir persamaan garis singgung yang melalui suatu titik dengan persamaan umum lingkaran.
Persamaan Garis Singgung yang Melalui Suatu Titik pada Lingkaran yang Berpusat di O(0,0)
Amati lingkaran pada Gambar 1. Titik \( A(x_1,y_1) \) terletak tepat pada lingkaran yang berpusat di O(0,0) dengan persamaan \( x^2 + y^2 = r^2 \). Dengan demikian, kita peroleh persamaan berikut
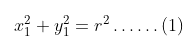

Gambar 1. Garis yang menyinggung lingkaran di titik A.
Jika dari titik \( A(x_1,y_1) \) dibuat garis \(g\) sedemikian hingga menyinggung lingkaran \( x^2 + y^2 = r^2 \) maka garis \(g\) tegak lurus OA. Misalkan gradien garis OA adalah \( m_{OA} \) dan gradien garis \(g\) adalah \(m_g\), maka diperoleh
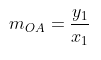
Garis OA tegak lurus garis \(g\), sehingga

Dengan demikian, persamaan garis \(g\) adalah

Dari persamaan (1) dan (2) didapat:
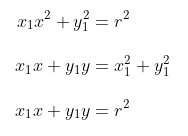
Jadi, persamaan garis singgung di titik \( (x_1,y_1) \) pada lingkaran \( x^2 + y^2 = r^2 \) adalah
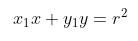
Perhatikan contoh soal berikut:
Contoh 1:
Tentukanlah persamaan garis singgung di titik (2,-3) pada lingkaran \(x^2+y^2=13\).
Pembahasan:
Sesuai dengan rumus persamaan garis singgung lingkaran \(x^2+y^2=r^2\) di \((x_1,y_1)\) maka persamaan garis singgung lingkaran \(x^2+y^2=13\) di (2,-3) adalah

Jadi, persamaan garis singgung di titik (2,-3) pada lingkaran \(x^2+y^2=13\) adalah \(2x – 3y = 13\).
Persamaan Garis Singgung yang Melalui Suatu Titik pada Lingkaran yang Berpusat di M(a,b)
Amati lingkaran pada Gambar 2. Suatu persamaan lingkaran C berpusat di (a,b) dan berjari-jari r dengan persamaan \( C: (x-a)^2 + (y-b)^2 = r^2 \), dan suatu titik \( A(x_1,y_1) \) pada C mempunyai persamaan garis singgung g di \( A(x_1,y_1) \).
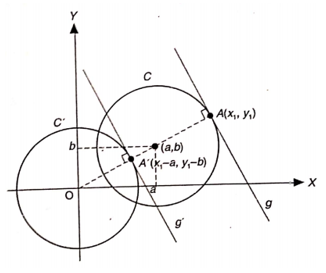
Gambar 2. Garis singgung menyinggung lingkaran \( (x-a)^2 + (y-b)^2 = r^2 \) di titik \( A(x_1,y_1) \)
Dengan translasi \( \left( {\begin{array}{rr} -a \\ -b \end{array} } \right) \) terhadap \( C: (x-a)^2 + (y-b)^2 = r^2 \) maka diperoleh \( C': x^2 + y^2 = r^2 \). Adapun titik \( A(x_1,y_1) \) pada lingkaran C akan menjadi \( A'(x_1-a,y_1-b) \) pada \( C': x^2 + y^2 = r^2 \).
Berdasarkan rumus garis singgung lingkaran dengan pusat O(0,0) di A(x,y) maka persamaan garis singgung lingkaran \( x^2 + y^2 = r^2 \) di \( A'(x_1-a,y_1-b) \) adalah g' dengan persamaan \( (x_1-a)x + (y_1-b)y = r^2 \)
Oleh translasi berlawanan dari \( \left( {\begin{array}{rr} -a \\ -b \end{array} } \right) \), yaitu \( \left( {\begin{array}{rr} a \\ b \end{array} } \right) \) terhadap garis singgung g' maka diperoleh garis singgung g terhadap \( (x-a)^2 + (y-b)^2 = r^2 \) di \(A(x_1,y_1)\). Translasi \( \left( {\begin{array}{rr} a \\ b \end{array} } \right) \) terhadap \( (x_1-a)x + (y_1-b)y = r^2 \) menjadi garis dengan persamaan

Jadi, persamaan garis singgung di titik \( (x_1,y_1) \) pada lingkaran yang berpusat di M(a,b) adalah
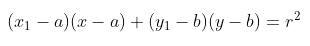
Perhatikan contoh soal berikut:
Contoh 2:
Tentukanlah persamaan garis singgung di titik (2,4) pada lingkaran \((x+4)^2+(y-5)^2=37\).
Pembahasan:
Persamaan garis singgung adalah

Jadi, persamaan garis singgung di titik (2,4) pada lingkaran \((x+4)^2+(y-5)^2=37\) adalah \(6x-y=8\).
Persamaan Garis Singgung yang Melalui Suatu Titik pada Lingkaran dengan Persamaan Bentuk Umumnya
Kita telah mempelajari bahwa bentuk umum dari persamaan lingkaran dapat dinyatakan sebagai
\[ x^2 + y^2 + 2Ax + 2By + C = 0 \]
Kita dapat mengubah bentuk umum persamaan lingkaran tersebut menjadi seperti berikut:
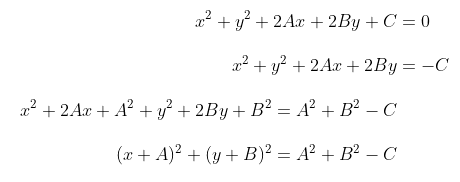
Persamaan garis singgung di titik \( A(x_1,y_1) \) adalah

Jadi, persamaan garis singgung di titik \( (x_1,y_1) \) pada lingkaran \( x^2 + y^2 + 2Ax + 2By + C = 0 \) adalah
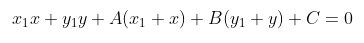
Perhatikan contoh soal berikut:
Contoh 3:
Tentukanlah persamaan garis singgung pada lingkaran \(x^2+y^2-6x+2y-3=0\) di titik yang berabsis 5.
Pembahasan:
\(x= 5\) disubstitusikan ke lingkaran \(x^2+y^2-6x+2y-3=0\)
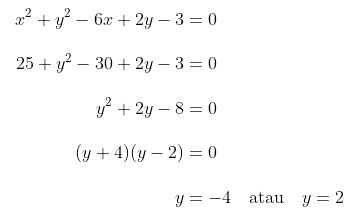
Diperoleh titik singgung A(5,-4) dan B(5,2).
Persamaan garis singgung adalah

Sehingga,
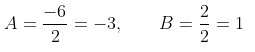
Dengan demikian,
Persamaan garis singgung di titik A(5,-4) adalah

Persamaan garis singgung di titik B(5,2) adalah

Jadi, persamaan garis singgung pada lingkaran tersebut adalah \( 2x-3y-22=0 \) dan \( 2x+3y-16=0 \).
Sumber:
Sunardi, Slamet Waluyo & Sutrisna. 2014. Konsep dan Penerapan Matematika SMA/MA Kelas XI. Jakarta: Penerbit PT Bumi Aksara.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Certain things catch your eye, but pursue only those that capture the heart.
