www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Lingkaran › Persamaan Garis Singgung Lingkaran dengan Gradien Tertentu
Persamaan Garis Singgung Lingkaran dengan Gradien Tertentu
Persamaan garis singgung pada lingkaran dapat dicari jika diketahui gradien dari garis singgung tersebut.
Kita telah mempelajari bagaimana mencari persamaan garis singgung yang melalui suatu titik pada lingkaran dan suatu titik di luar lingkaran. Namun, tak jarang informasi yang ada tidak menunjukkan letak titik tersebut melainkan hanya diketahui gradien dari garis singgung yang ingin kita cari. Jika demikian halnya, kita tidak bisa mencari persamaan garis singgung seperti yang telah kita bahas.
Oleh karena itu, pada artikel ini kita akan belajar bagaimana mencari persamaan garis singgung pada lingkaran jika diketahui gradien dari garis singgung tersebut.
Persamaan Garis Singgung dengan Gradien m terhadap Lingkaran yang Berpusat di O(0,0)
Sebagaimana telah kita pelajari bahwa persamaan lingkaran yang berpusat di O(0,0) adalah \( x^2 + y^2 = r^2 \). Persamaan garis singgung terhadap lingkaran \( x^2 + y^2 = r^2 \) dengan gradien \(m\) dapat ditentukan sebagai berikut:
- Misalkan persamaan garis dengan gradien \(m\) adalah \( y = mx + n \)
- Substitusikan \( y = mx + n \) ke persamaan lingkaran \( x^2 + y^2 = r^2 \), sehingga diperoleh
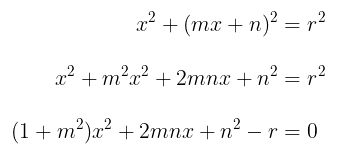
Dapat Anda lihat bahwa persamaan ini adalah suatu persamaan kuadrat dengan variabel x. Garis menyinggung lingkaran, artinya diskriman dari persamaan kuadrat tersebut sama dengan nol (persamaan kuadrat mempunyai akar kembar).
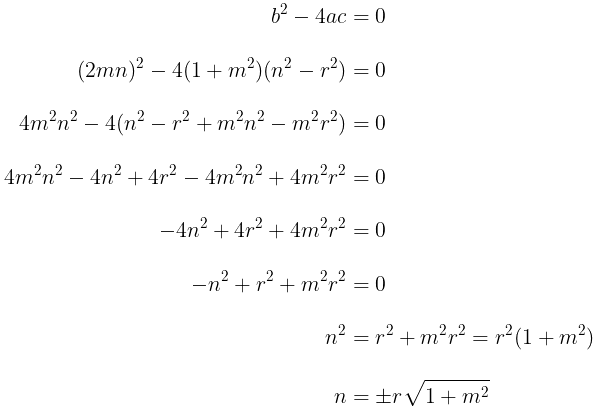
Setelah itu, \(n\) disubstitusikan ke dalam persamaan garis \( y = mx + n \).
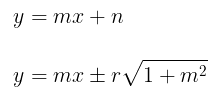
Jadi, persamaan garis singgung dengan gradien \(m\) terhadap lingkaran \( x^2 + y^2 = r^2 \) adalah
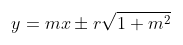
Perhatikan contoh soal berikut:
Contoh 1:
Tentukanlah persamaan garis singgung yang bergradien -2 terhadap lingkaran \(x^2+y^2=16\).
Pembahasan:
Diketahui: \(m = -2\) dan \(r = 4\). Dengan demikian,
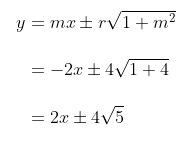
Jadi, persamaan garis singgungnya adalah \( y = -2x + 4\sqrt{5} \) dan \( y = -2x - 4\sqrt{5} \)
Persamaan Garis Singgung dengan Gradien \(m\) terhadap Lingkaran yang Berpusat di M(a,b)
Kita tahu bahwa lingkaran yang berpusat di M(a,b) mempunyai persamaan \( (x-a)^2 + (y-b)^2 = r^2 \). Sekarang amatilah Gambar 1!. Lingkaran \( (x-a)^2 + (y-b)^2 = r^2 \) mempunyai garis singgung g.
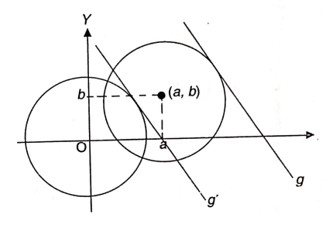
Gambar 1. Garis singgung dengan gradien m terhadap lingkaran \( (x-a)^2 + (y-b)^2 = r^2 \)
- Jika lingkaran \( (x-a)^2 + (y-b)^2 = r^2 \) ditranslasikan dengan \( \left( {\begin{array}{rr} -a \\ -b \end{array} } \right) \) maka diperoleh lingkaran dengan persamaan \( x^2 + y^2 = r^2 \) dan garis g menjadi g' (garis singgung di \( x^2 + y^2 = r^2 \)).
- Persamaan garis singgung dengan gradien m pada lingkaran \( x^2 + y^2 = r^2 \) adalah g' dengan persamaan:
- Jika garis g' ditranslasikan dengan \( \left( {\begin{array}{rr} -a \\ -b \end{array} } \right) \) maka akan menjadi garis g dengan persamaan
- Jadi, persamaan garis singgung dengan gradien m pada lingkaran \( (x-a)^2 + (y-b)^2 = r^2 \) adalah
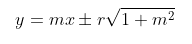
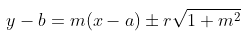
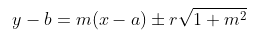
Contoh 2:
Tentukanlah persamaan garis singgung pada lingkaran \(x^2+y^2-6x+8y+9=0\) yang tegak lurus dengan garis \(4x – 3y + 7 = 0\).
Pembahasan:
Langkah-langkah penyelesaiannya adalah sebagai berikut:
- Persamaan bentuk umum lingkaran diubah ke dalam persamaan lingkaran yang dapat diketahui pusat dan jari-jarinya sehingga:
- Tentukan gradien dari persamaan garis \( 4x-3y + 7 = 0 \)
- Tentukan persamaan garis singgung dengan menggunakan gradien garis \( m_2 \) yang telah diperoleh, yaitu
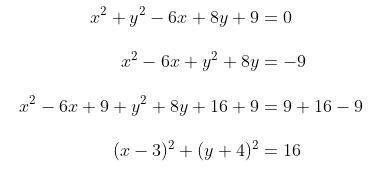
Didapatkan:
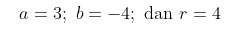
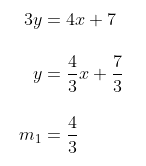
Persamaan garis singgung yang akan dicari tegak lurus dengan garis 4x - 3y + 7 = 0. Diketahui syarat garis saling tegak lurus adalah \( m_1 \cdot m_2 = -1 \) maka didapat
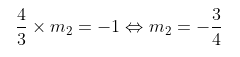
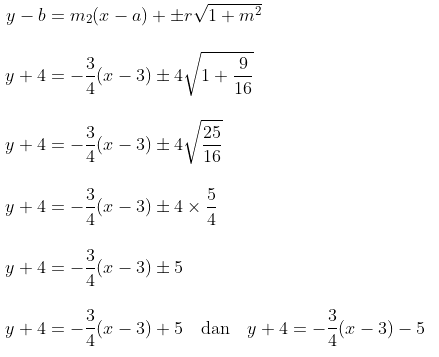
atau
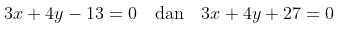
Sumber:
Sunardi, Slamet Waluyo & Sutrisna. 2014. Konsep dan Penerapan Matematika SMA/MA Kelas XI. Jakarta: Penerbit PT Bumi Aksara.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
You often feel tired, not because you've done too much, but because you've done too little of what sparks a light in you.
