Matematika Dasar   »   Lingkaran   ›  Persamaan Garis Singgung Lingkaran yang Melalui Suatu Titik di Luar Lingkaran

Lingkaran

Persamaan Garis Singgung Lingkaran yang Melalui Suatu Titik di Luar Lingkaran

Untuk mencari persamaan garis singgung yang melalui suatu titik di luar lingkaran, kita perlu mencari persamaan garis kutub atau garis polar terlebih dahulu.

Oleh Tju Ji Long · Statistisi

Hub. WA: 0812-5632-4552

Pada bagian ini akan dibahas persamaan garis singgung yang melalui suatu titik di luar lingkaran. Untuk mencari persamaan garis singgung ini, pertama kita perlu mencari persamaan garis kutub atau garis polar terlebih dahulu. Oleh karena itu, kita akan mengawali pembahasan mengenai bagaimana mencari persamaan garis kutub atau garis polar pada lingkaran.

Persamaan garis kutub atau garis polar titik \( P(x_1,y_1) \) terhadap lingkaran \( x^2 + y^2 = r^2 \)

Amati Gambar 1. Titik \( P(x_1,y_1) \) terletak di luar lingkaran \( x^2 + y^2 = r^2 \). Jika dari titik P dibuat garis g dan h sehingga menyinggung lingkaran di titik A dan B maka garis AB disebut garis kutub atau garis polar titik \( P(x_1,y_1) \).

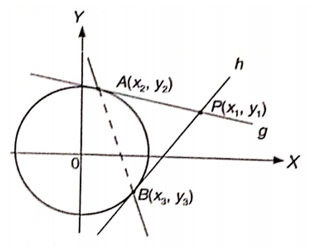
Gambar 1. Garis singgung melalui suatu titik di luar lingkaran

Dari Gambar 1, kita peroleh beberapa hal sebagai berikut:

1. Persamaan garis singgung di titik \( A(x_2,y_2) \) pada lingkaran \( x^2 + y^2 = r^2 \) adalah garis g (garis AP) yang mempunyai persamaan \( x_2x + y_2y = r^2 \). Karena titik \( P(x_1,y_1) \) pada garis g maka berlaku \( x_2x_1 + y_2y_1 = r^2 \). Hal ini berarti bahwa titik \( A(x_2,y_2) \) terletak pada garis:

2. Persamaan garis singgung di titik \( B(x_3,y_3) \) pada lingkaran \( x^2 + y^2 = r^2 \) adalah garis h (garis BP) yang mempunyai persamaan \( x_3x + y_3y = r^2 \). Karena titik \( P(x_1,y_1) \) pada garis h maka berlaku \( x_3x_1 + y_3y_1 = r^2 \). Hal ini berarti bahwa titik \( B(x_3,y_3) \) terletak pada garis:

3. Dari persamaan (1) dan (2), diperoleh kesimpulan bahwa persamaan garis \( AB \), adalah

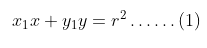
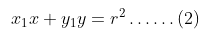
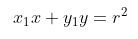
Berdasarkan keterangan di atas, berlaku pula sebagai berikut:

1. Persamaan garis kutub titik \( P(x_1,y_1) \) terhadap lingkaran \( (x-a)^2 + (y-b)^2 = r^2 \) adalah

2. Persamaan garis kutub titik \( P(x_1,y_1) \) terhadap lingkaran \( x^2 + y^2 + 2Ax + 2By + C = 0 \) adalah

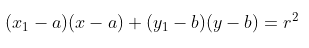
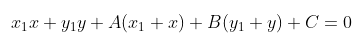
Persamaan garis singgung dari titik \( P(x_1,y_1) \) di luar lingkaran

Untuk menentukan persamaan garis singgung dari titik \( P(x_1,y_1) \) di luar lingkaran, diperlukan langkah-langkah sebagai berikut:

1. Menentukan persamaan garis kutub titik \( P(x_1,y_1) \) terhadap lingkaran
2. Menentukan koordinat titik potong antara garis kutub dan lingkaran
3. Menentukan persamaan garis singgung di tiap titik potong antara garis kutub dan lingkaran

Agar anda memahami langkah-langkah tersebut, perhatikan contoh soal berikut.

Contoh 1:

Tentukanlah persamaan garis singgung pada lingkaran \(x^2+y^2=9\) dari titik (0,5) yang terletak di luar lingkaran!

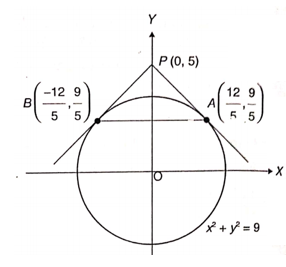
Gambar 2. Garis singgung lingkaran \( x^2 + y^2 = 9 \) dari titik di luar lingkaran.

Pembahasan:

Persamaan garis kutub di titik (0,5) terhadap lingkaran \(x^2+y^2=9\) adalah

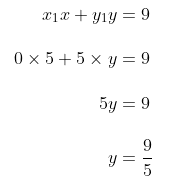
Perpotongan garis \( y = \frac{9}{5} \) dengan lingkaran \(x^2+y^2=9\) ditentukan dengan mensubstitusikan garis \( y = \frac{9}{5} \) pada lingkaran \(x^2+y^2=9\), yakni

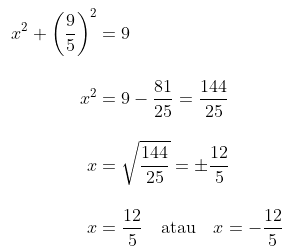
Sehingga diperoleh titik potong

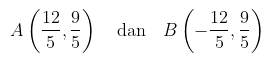
Persamaan garis singgung di A adalah

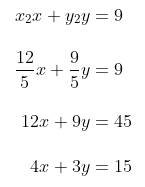
Persamaan garis singgung di B adalah

Jadi, persamaan garis singgung pada lingkaran tersebut adalah \( 4x+3y=15 \) dan \( 4x-3y=-15 \).

Cukup sekian penjelasan mengenai persamaan garis singgung lingkaran yang melalui suatu titik di luar lingkaran dalam artikel ini. Semoga bermanfaat.

Sumber:

Sunardi, Slamet Waluyo & Sutrisna. 2014. Konsep dan Penerapan Matematika SMA/MA Kelas XI. Jakarta: Penerbit PT Bumi Aksara.

Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan tuliskan komentar Anda dengan bahasa yang sopan.