www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Statistika › Ukuran Lokasi: Quartil
Ukuran Lokasi: Quartil
Kuartil adalah ukuran letak yang membagi data atau sekumpulan nilai yang sudah diurutkan dari data terkecil hingga terbesar menjadi empat bagian yang sama.
Sekumpulan nilai yang sudah diurutkan dari data terkecil hingga terbesar dapat dibagi menjadi empat bagian. Ukuran letak yang membagi data tersebut menjadi 4 bagian yang sama dinamakan kuartil. Oleh karena itu, masing-masing bagian mengandung 25% data.
Pada sekumpulan data mempunyai tiga buah kuartil, yaitu:
- Kuartil bawah atau kuartil ke-1 (\(Q_1\))
- Kuartil tengah atau kuartil ke-2 atau median (\(Q_2\)), dan
- Kuartil atas atau kuartil ke-3 (\(Q_3\))

Untuk menentukan nilai kuartil dari sekumpulan data yang tidak dikelompokkan, ditempuh langkah-langkah sebagai berikut.
- Urutkan data dari nilai terkecil hingga terbesar
- Tentukan letak kuartil-kuartilnya dengan rumus berikut.
- \(Q_1\) pada data urutan ke ¼ (n+1)
- \(Q_2\) pada data urutan ke ½ (n+1)
- \(Q_3\) pada data urutan ke ¾ (n+1)
Jika nomor urutan tersebut bukan bilangan cacah maka harus digunakan interpolasi. Perhatikan contoh soal berikut.
Contoh 1: Kuartil
Tentukan kuartil bawah \( (Q_1) \), kuartil tengah \( (Q_2) \), dan kuartil atas \( (Q_3) \) dari sekumpulan data berikut: 70, 50, 50, 70, 40, 80, 50, 90, 60, 50, 40.
Pembahasan:
Data diurutkan dari nilai terkecil hingga terbesar.
Tampak bahwa: Kuartil bawah \( (Q_1) = 50 \), kuartil \( (Q_2) = 50 \) dan kuartil atas \( (Q_3) = 70 \) membagi kelompok data ini atas 4 bagian yang sama. Amatilah bahwa \( Q_2 \) membagi data atas dua bagian, masing-masing memuat lima nilai. Begitupun \( Q_1 \) membagi lima nilai yang pertama atas dua bagian yang lain, masing-masing memuat dua nilai, demikian juga \( Q_3 \).
Contoh 2: Kuartil
Tentukan kuartil bawah, kuartil tengah, dan kuartil atas dari data pada tabel berikut!
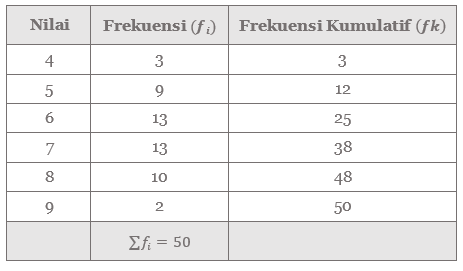
Pembahasan:
Letak kuartil bawah \( (Q_1) \) pada data urutan
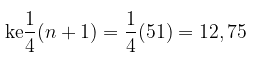
Letak kuartil tengah \( (Q_2) \) pada data urutan
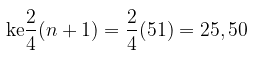
Letak kuartil atas \( (Q_3) \) pada data urutan
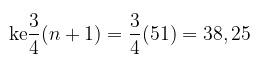
Karena nomor urutan bukan bilangan cacah maka digunakan interpolasi. Sehingga, diperoleh:
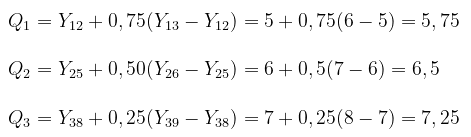
Selanjutnya, untuk menentukan nilai kuartil data yang sudah dikelompokkan ke dalam tabel distribusi frekuensi, digunakan rumus:

Keterangan:
\(Q_j\) = desil ke-j (j = 1, 2, 3, …,99)
\(Tb_{Q_j}\) = tepi bawah kelas yang memuat \(Q_j\)
\(n\) = jumlah seluruh frekuensi
\(fk_{Q_j}\) = frekuensi kumulatif kurang dari di bawah kelas yang memuat \(Q_j\)
\(f_{Q_j}\) = frekuensi kelas yang memuat \(Q_j\)
\(I\) = lebar atau panjang kelas (interval kelas)
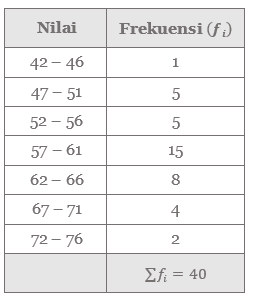
Contoh 3: Kuartil Data Berkelompok
Nilai pelajaran Matematika dari 40 orang siswa dikelompokkan seperti ditunjukkan pada tabel berikut di bawah. Tentukan: (a) kuartil bawah, (b) kuartil tengah, dan (c) kuartil atas!
Pembahasan:
Tabel nilai matematika di atas dilengkapi dengan nilai yang diperlukan sehingga menjadi seperti tabel berikut.
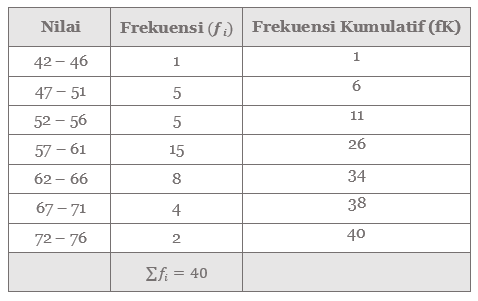
(a) Kuartil bawah atau kuartil ke-1 \( (Q_1) \)
Untuk menentukan nilai \( (Q_1) \), tentukan dulu kelas yang memuat \( Q_1 \), yaitu dengan menghitung nilai dari
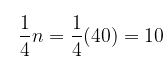
Berarti, kelas yang memuat \( Q_1 \) adalah 52 - 56, dengan \( fk = 1 \) maka diperoleh
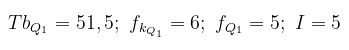
Sehingga kuartil bawahnya:
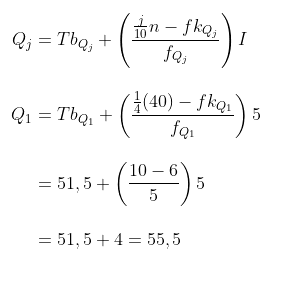
Jadi, kuartil bawahnya adalah 55,5.
(b) Kuartil tengah atau kuartil ke-2 \( (Q_2) \)
Untuk menentukan nilai \( (Q_2) \), tentukan dulu kelas yang memuat \( Q_2 \), yaitu dengan menghitung nilai dari

Berarti, kelas yang memuat \( Q_2 \) adalah 57 - 61, dengan \( fk = 15 \) maka diperoleh
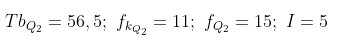
Sehingga kuartil tengahnya:
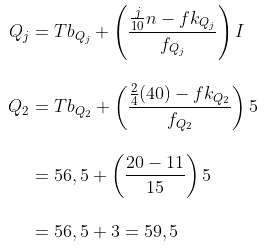
Jadi, kuartil tengahnya adalah 59,5.
(c) Kuartil atas atau kuartil ke-3 \( (Q_3) \)
Untuk menentukan nilai \( (Q_3) \), tentukan dulu kelas yang memuat \( Q_3 \), yaitu dengan menghitung nilai dari
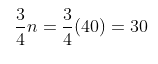
Berarti, kelas yang memuat \( Q_3 \) adalah 62 - 66, dengan \( fk = 34 \) maka diperoleh

Sehingga kuartil atasnya:
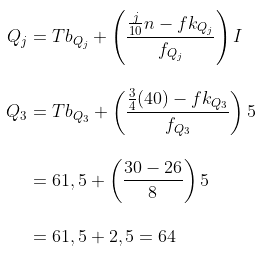
Jadi, kuartil atasnya adalah 64.
Sumber:
Sunardi, Slamet Waluyo & Sutrisna. 2014. Konsep dan Penerapan Matematika SMA/MA Kelas XI. Jakarta: Penerbit PT Bumi Aksara.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
When someone loves you, the way they talk about you is different. You feel safe and comfortable.
