www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Geometri › Dua Garis yang Saling Sejajar
Dua Garis yang Saling Sejajar
Dua garis dikatakan sejajar apabila kedua garis tersebut terletak pada satu bidang datar dan tidak akan pernah berpotongan jika kedua garis tersebut diperpanjang sampai tak terhingga.
Dua garis atau lebih dikatakan sejajar apabila garis-garis tersebut terletak pada satu bidang datar dan tidak akan pernah bertemu atau berpotongan jika garis tersebut diperpanjang sampai tak terhingga. Dua garis sejajar dinotasikan dengan “//”.
Perhatikan Gambar 1 berikut.

Gambar 1. (a) Dua garis yang saling sejajar; (b) Dua garis yang tidak saling sejajar
Pada Gambar 1.a, garis g dan garis h dikatakan saling sejajar dan dinotasikan dengan \(g//h\). Akan tetapi, garis m dan n pada Gambar 1.b tidak sejajar, karena jika garis-garis tersebut diperpanjang sampai titik tertentu, maka kedua garis tersebut akan saling berpotongan.
Dua Garis Sejajar yang Berpotongan dengan Garis Lain
Jika dua buah garis sejajar dipotong oleh sebuah garis lain, maka akan terbentuk beberapa macam pasangan sudut, yakni sudut sehadap, sudut dalam berseberangan, sudut luar berseberangan, sudut dalam sepihak, dan sudut luar sepihak.
Pada Gambar 2 di bawah, tampak dua garis lurus sejajar (garis g dan garis h) yang dipotong oleh sebuah garis lain sehingga terbentuk delapan sudut, yaitu
\[∠P_1, ∠Q_1, ∠P_2, ∠Q_2, ∠P_3, ∠Q_3, ∠P_4, ∠Q_4\]
Dalam hal ini berlaku:
- \(∠P_1\) sehadap dengan \( ∠Q_1 \) sehingga \( ∠P_1 = ∠Q_1 \)
- \(∠P_2\) sehadap dengan \( ∠Q_2 \) sehingga \( ∠P_2 = ∠Q_2 \)
- \(∠P_3\) sehadap dengan \( ∠Q_3 \) sehingga \( ∠P_3 = ∠Q_3 \)
- \(∠P_4\) sehadap dengan \( ∠Q_4 \) sehingga \( ∠P_4 = ∠Q_4 \)
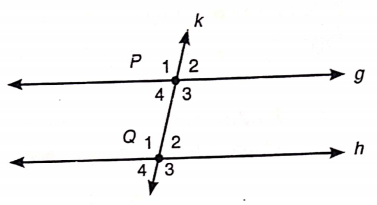
Gambar 2. Garis k memotong garis g dan h yang saling sejajar
Jadi, dapat disimpulkan bahwa jika dua garis sejajar dipotong oleh garis lain maka akan terbentuk empat pasang sudut sehadap yang besarnya sama.
Sekarang amati kembali Gambar 2 dan lihatlah sudut \(∠P_3\) dan \(∠Q_1\) serta \(∠P_4\) dan \(∠Q_2\). Pasangan sudut ini disebut pasangan sudut dalam bersebarangan dan besarnya sudut yang terbentuk adalah sama besar. Sekali lagi, lihatlah \(∠P_1\) dan \(∠Q_3\) serta \(∠P_2\) dan \(∠Q_4\). Pasangan sudut ini disebut pasangan sudut luar berseberangan dan besar sudut yang terbentuk adalah sama besar.
Jadi, dapat disimpulkan bahwa jika dua garis sejajar dipotong oleh garis lain maka besar sudut-sudut dalam dan luar berseberangan yang terbentuk adalah sama besar.
Pasangan sudut lain pada Gambar 2 adalah pasangan sudut dalam sepihak dan luar sepihak. Pada sudut sepihak berdasarkan Gambar 2 adalah \(∠P_4\) dan \(∠Q_1\) serta \(∠P_3\) dan \(∠Q_2\). Jumlah besar sudut untuk pasangan sudut dalam sepihak adalah 1800. Sementara itu, pasangan sudut luar sepihak yaitu \(∠P_1\) dan \(∠Q_4\) serta \(∠P_2\) dan \(∠Q_3\). Jumlah besar sudut untuk pasangan sudut luar sepihak adalah 1800.
Gradien Dua Garis yang Sejajar
Amati Gambar 3! Terdapat dua persamaan garis lurus yaitu \(y = x + 2\) dan \(y = x – 1\). Apakah kedua garis yang terbentuk merupakan dua garis yang sejajar? Bagaimanakah Anda dapat membuktikan bahwa kedua persamaan tersebut sejajar?

Gambar 3. Grafik dua persamaan sejajar
Untuk menjawab pertanyaan ini, Anda dapat menguji gradien masing-masing garis tersebut dengan mengambil dua titik sembarang yang melalui masing-masing garis. Misalkan untuk garis \(g\) melalui titik \(A(-2,0)\) dan \(B(0,2)\), maka gradien garis \(g\) (\(m_1\)) adalah

Demikian pula, untuk garis \(h\) melalui titik \(C(0,-1)\) dan \(D(0,1)\), maka gradien garis \(h \ (m_2)\) adalah

Ternyata, \(m_1 = m_2 = 1\). Jadi, kedua garis tersebut sejajar.
Dengan demikian, dari persamaan di atas dapat disimpulkan sebagai berikut.
Definisi: Gradien Dua Garis Sejajar
Jika \(y_1 = m_1x + c_1\) dan \(y_2 = m_2x + c_2\) merupakan persamaan garis yang saling sejajar, maka besar gradien garis tersebut adalah sama. Secara matematis dapat ditulis:

Beberapa contoh berikut akan membantu kita memahami materi yang telah kita jelaskan di atas.
Contoh 1:
Tentukan persamaan garis yang melalui titik (5,1) dan sejajar garis \(2y = 4x – 3\).
Pembahasan:
Penulisan persamaan garis ada dua, yaitu:
- Bentuk implisit: \(ax + by = c\); gradien = \(m = - a/b\).
- Bentuk eksplisit: \(y = mx + n\); gradien = \(m\).
Diketahui garis dengan persamaan: \(2y = 4x – 3\), maka

Karena kedua garis dianggap sejajar maka berlaku: \(m_1 = m_2\) sehingga diperoleh:
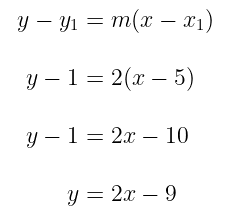
Jadi, persamaan garis tersebut adalah \(y = 2x – 9\).
Sumber:
Sunardi, Slamet Waluyo & Sutrisna. 2014. Konsep dan Penerapan Matematika SMA/MA Kelas XI. Jakarta: Penerbit PT Bumi Aksara.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
Sebuah permata tidak akan dapat dipoles tanpa gesekan, demikian juga seseorang tidak akan menjadi sukses tanpa tantangan.
