www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Matematika Dasar » Geometri › Dua Garis yang Saling Berpotongan
Dua Garis yang Saling Berpotongan
Dua garis dikatakan saling berpotongan apabila kedua garis terletak pada satu bidang datar dan berpotongan hanya di satu titik. Dua garis yang berpotongan dapat membentuk dua pasang sudut yang saling bertolak belakang.
Dua garis dikatakan berpotongan apabila dua garis tersebut terletak pada satu bidang datar dan kedua garis tersebut berpotongan hanya di satu titik. Coba amati Gambar 1 di bawah ini.

Gambar 1. Dua garis berpotongan pada satu titik
Sudut yang Terbentuk dari Dua Garis yang Berpotongan
Dua garis yang berpotongan dapat membentuk dua pasang sudut yang saling membelakangi atau saling bertolak belakang. Besar dua sudut yang saling bertolak belakang adalah sama besar. Amati Gambar 2!

Gambar 2. Dua garis berpotongan
Pada Gambar 2, tampak bahwa dua garis saling berpotongan. Jika diketahui:
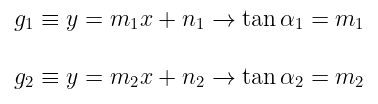
Dengan demikian, besar sudut yang dibentuk oleh garis \(g_1\) dan \(g_2\) (φ) adalah \((∠φ=α_1-α_2)\):
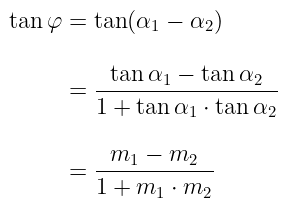
Jadi, sudut antara g1 dan g2 dapat ditentukan dengan rumus:
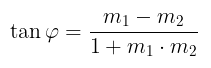
di mana: \(φ\) = sudut yang dibentuk oleh garis \(g_1\) dan \(g_2\); \(m_1\) = gradien garis \(g_1\); \(m_2\) = gradien garis \(g_2\).
Setelah besar \(φ\) diperoleh maka dapat diperoleh hubungan berikut.
- Jika \(\tan φ > 0\), berarti \(φ\) bersudut lancip, dan
- Jika \(\tan φ< 0\), berarti \(φ\) bersudut tumpul.
Dua Garis Berpotongan Tegak Lurus
Jika dua garis (\(g_1\) dan \(g_2\)) berpotongan dan membentuk sudut \(90^0\) (sudut siku-siku, \(∠φ=90^0\)) maka dapat dikatakan bahwa kedua garis tersebut berpotongan tegak lurus (Gambar 3). Sehingga diperoleh:
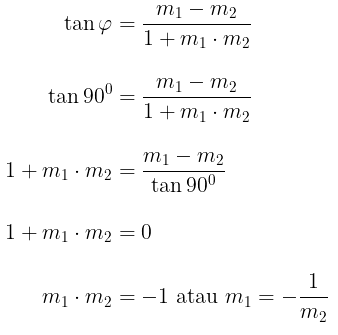
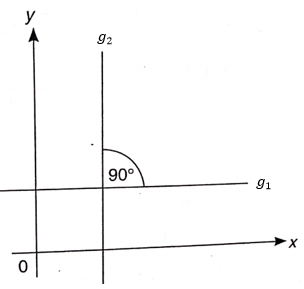
Gambar 3. Dua garis berpotongan tegak lurus
Dengan demikian, dua garis dikatakan saling berpotongan tegak lurus (⊥), jika memenuhi

Beberapa contoh berikut ini akan membantu kita memahami materi mengenai dua garis yang saling berpotongan.
Contoh 1:
Tentukan persamaan garis \(g\) yang melalui titik (-2,4) dan tegak lurus garis h dengan persamaan \( 3y= x - 6 \).
Pembahasan:
Diketahui garis \( h ≡ 3y = x - 6 \), maka
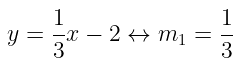
Karena garis \( g ⊥ h \), maka diperoleh:
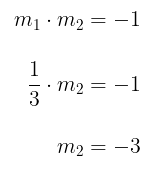
Sehingga, persamaan garis \(g\) adalah
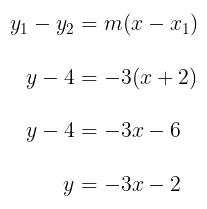
Jadi, persamaan garis \(g\) adalah \( y = -3x - 2 \).
Sumber:
Sunardi, Slamet Waluyo & Sutrisna. 2014. Konsep dan Penerapan Matematika SMA/MA Kelas XI. Jakarta: Penerbit PT Bumi Aksara.
Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel Terkait
When you judge others, you do not define them; you define yourself.
